Robust Factor Graphs for GNSS Localization in Urban Environments
Introduction
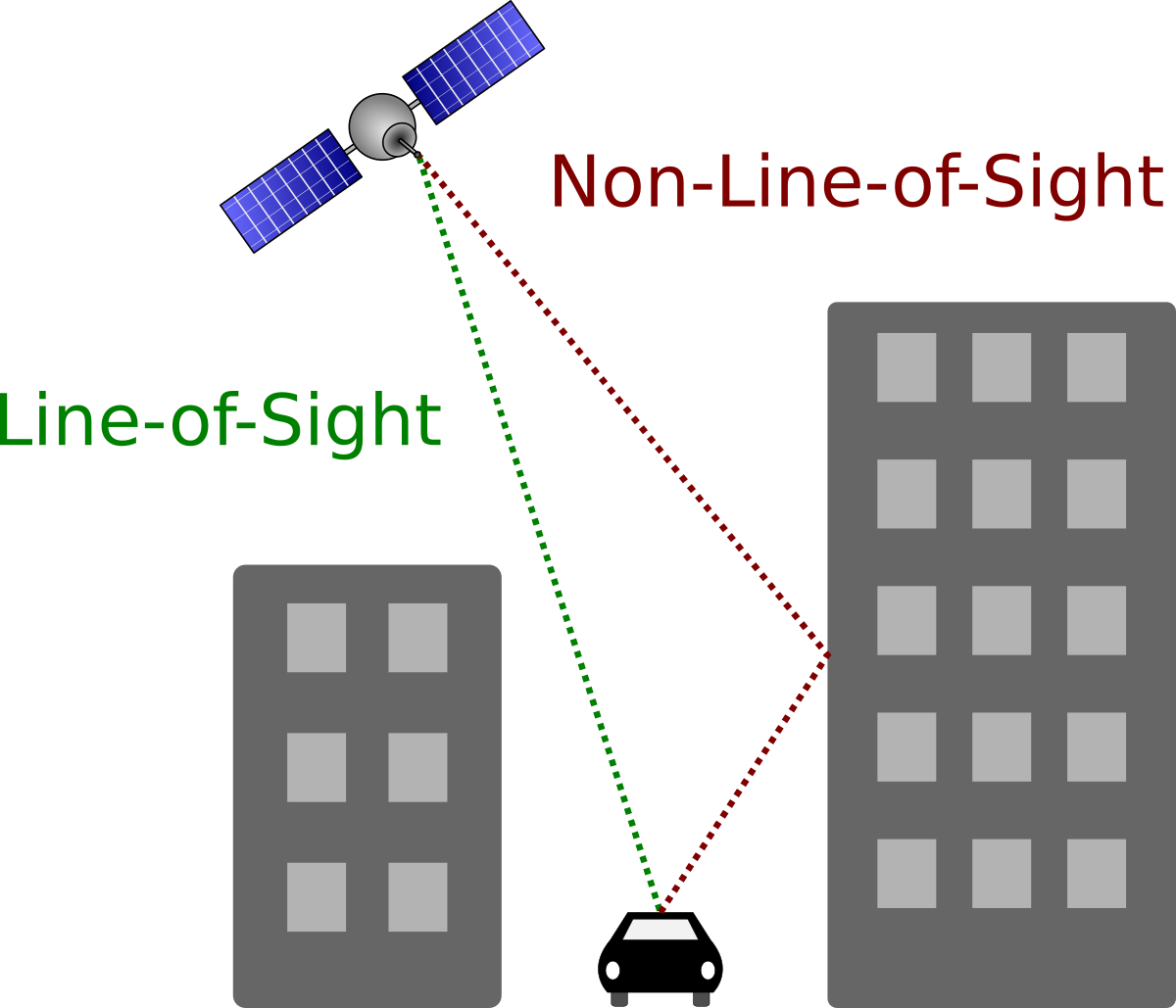
A common challenge for vehicle localization based on global navigation satellite systems (GNSS) is the multipath or on line of sight (NLOS) problem.
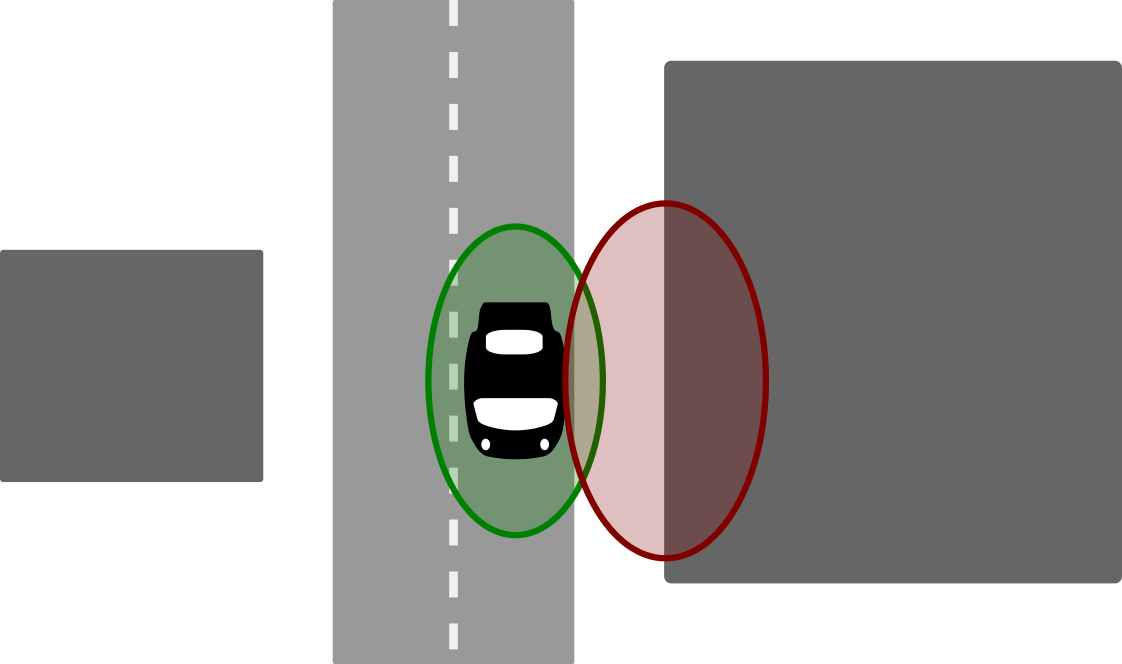
This problem occurs for instance in urban areas with high buildings: Although the direct line of sight (LOS) to a satellite is blocked by a building, its signal may still reach the receiver on the ground via one or several reflections on building structures or the ground. Since the signal path is longer for the reflected signal, ranging errors occur that can either prolongate the observed pseudorange or, due to correlation effects, shorten it.
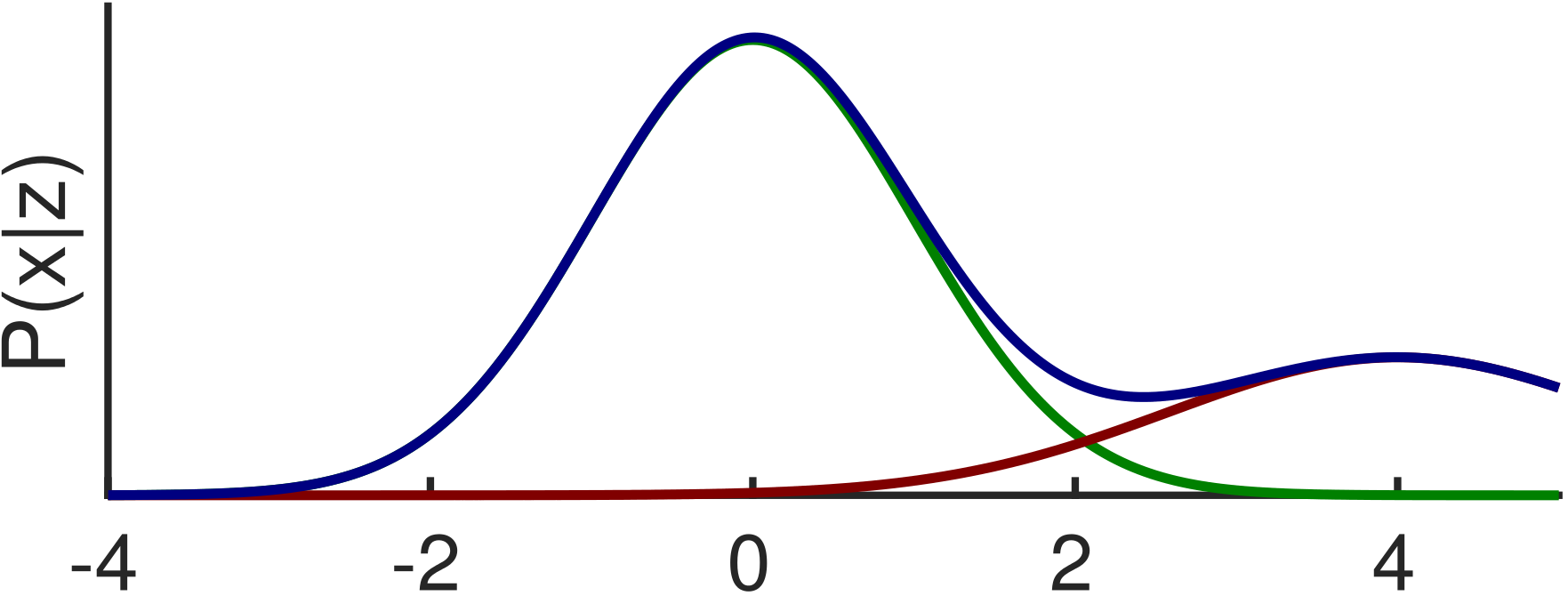
Multipath effects can also occur when the direct line of sight is free. In this situation, the signal is received directly, but is also reflected on a building or another structure in the vicinity of the receiver. Hence, the signal is received multiple times, leading to correlation errors. The observations that are subject to multipath effects can be considered outliers that can severely bias the least squares estimate of the receiver's position. Even a single multipath measurement can lead to a defective position estimate. The problem gets worse if one considers that in urban environments not only one, but several satellite observations might be affected by multipath effects.
Along with a distorted estimate of the receivers position, the estimated covariance is also erroneous. The estimator calculates a too small uncertainty under the assumption of Gaussian noise, that NLOS measurements violates. This inconsistency makes it even more difficult to recover the true estimate through including other sensors. A consistent estimator have to rise its covariance if its estimate is less accurate.
Our Approach
Recent developments in factor graph based optimization methods in the field of mobile robotics can be transferred to the domain of GNSS-based localization. Here, we see two possible strategies to deal with the multipath effects. If only a position estimate is necessary, a binary decision is possible to classify a pseudorange measurement either as inlier or outlier. If additional information about the covariance of the position estimate is needed, this is not sufficient. Here we need to model the pseudorange measurements including the multipath effects, to get a consistent covariance matrix.
Following the above categorisation, we distinguish between a sole robust factor graph based optimization method called switchable constraints and a generalized method including a correct error distribution.
Generalized Method
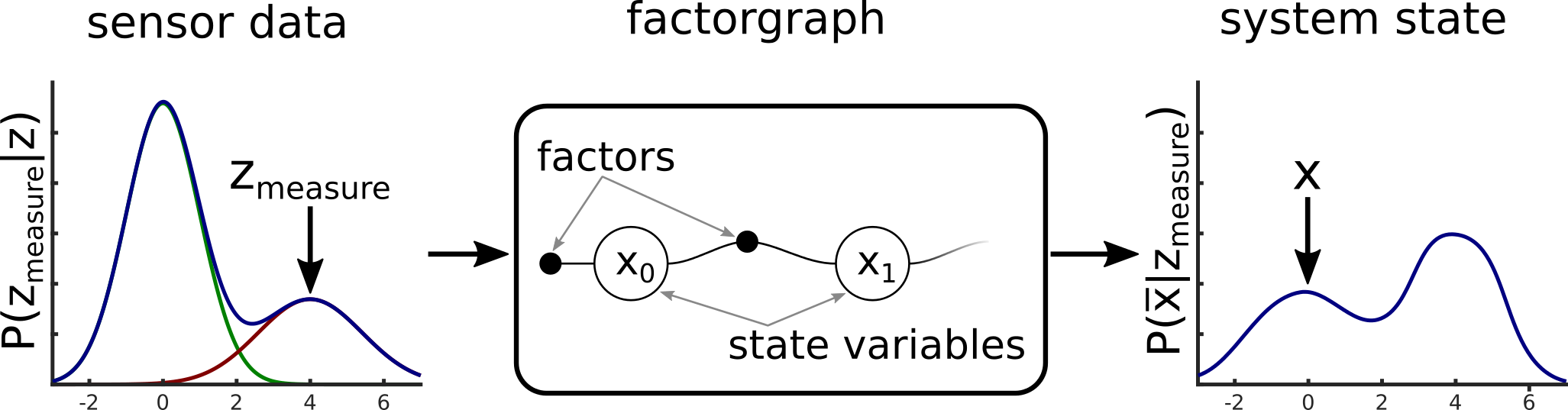
In our recent project smartLoc we focus on a better description of the error distributions that multipath effects can cause. Through modelling these non-Gaussian and multimodal inside the factorgraph we aim to improve the estimation result as well as the corresponding covariance. Our recent results (see this paper) show the big potential of this approach.
Switchable Constraints
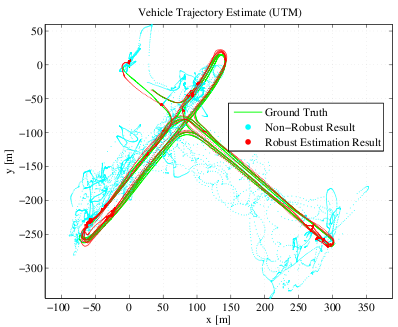
Our past work transfered advances in robust optimization from the field of SLAM (Simultaneous Localization and Mapping) in robotics to the domain of GNSS-based localization. The methods developed there are very versatile and can be applied to other least squares problems where outliers have to be expected. Therefore, we could successfully transfer the gained insights from SLAM into the domain of GNSS-based localization.
Our papers (see below) demonstrate how multipath observations can be identified and rejected during the least squares optimization that solves for the position estimate, without additional a priori knowledge or additional sensor information. We provide an introduction to factor graphs and how the GNSS-based localization problem can be expressed using such a graph structure. This will help the reader to understand the key idea of the proposed robust optimization scheme. The image on the right presents results acquired from a real-world dataset and compares our proposed solution against a highly accurate ground truth.
Publications
- (2016) The Problem of Comparable GNSS Results — An Approach for a Uniform Dataset with Low-Cost and Reference Data. In Proc. of Intl. Conf. on Advances in Vehicular Systems (VEHICULAR). ISBN: 978-1-61208-515-9
- (2016) Robust Factor Graph Optimization — A Comparison for Sensor Fusion Applications. In Proc. of Intl. Conf. on Emerging Technologies and Factory Automation (ETFA). DOI: 10.1109/ETFA.2016.7733598
- (2013) Switchable Constraints and Incremental Smoothing for Online Mitigation of Non-Line-of-Sight and Multipath Effects. In Proc. of IEEE Intelligent Vehicles Symposium (IV). DOI: 10.1109/IVS.2013.6629480
- (2012) Multipath Mitigation in GNSS-Based Localization using Robust Optimization. In Proc. of IEEE Intelligent Vehicles Symposium (IV). DOI: 10.1109/IVS.2012.6232299
- (2012) Towards Robust Graphical Models for GNSS-Based Localization in Urban Environments. In Proc. of IEEE International Multi-Conference on Systems, Signals and Devices (SSD). DOI: 10.1109/SSD.2012.6198059
- (2012) Robust Optimization for Simultaneous Localization and Mapping. Dissertation: Chemnitz University of Technology
