Automation Technology
Learning Vector Symbolic Architectures

Vector Symbolic Architectures

Vector Symbolic Architectures (VSA) combine a hypervector space and a set of operations on these vectors. Hypervectors provide powerful and noise-robust representations and VSAs are associated with promising theoretical properties for approaching high-level cognitive tasks.

Tutorials on Vector Symbolic Architectures

  • We organized a free online tutorial on VSAs during the European Conference on Artificial Intelligence (ECAI) in 2020. More information, slides and supplemental material can be found on our tutorial website.
ECAI 2020 logo

  • We organized a half-day tutorial on VSAs during the German Conference on Artifical Intelligence (KI) in 2019. More information, slides and supplemental material can be found on our tutorial website.
KI 2019 logo

Our work on Vector Symbolic Architectures

An introduction to our work on VSAs was recently given by Peer Neubert during the Online Webinars on Developments in Hyperdimensional Computing and Vector-Symbolic Architectures:

References

An introduction to Vector Symbolic Architectures

Vector Symbolic Architectures (VSA) combine a hypervector space and a set of operations on these vectors. Hypervectors provide powerful and noise-robust representations and VSAs are associated with promising theoretical properties for approaching high-level cognitive tasks.

Hypervectors - The upside of the curse of dimensionality

scheme.jpg

Hypervectors are high dimensional vectors, typically with more than 1,000 dimensions. They can be sparse or dense, binary, ternary, or real-valued. Who ever tried something like a nearest-neighbour classifier in spaces with more than a few (e.g. 10) dimensions, likely encountered the curse of dimensionality: algorithms that work well in low dimensional spaces often fail when faced with high dimensional data.

So, high dimensional spaces are bad and should always be avoided? Not at all. High dimensional representations are omnipresent, in particular in massively parallel biological processing systems and there are at least two properties that can be exploited in technical (i.e. algorithmic) applications:
  • The capacity of a hypervector is enormous (even if it's sparse and binary).
  • The number of almost orthogonal vectors is exponential in the number of dimensions.
The benefit of the first property is straight forward. The latter basically says that two randomly chosen (or unrelated) vectors are very likely to be almost orthogonal. This property can be used, e.g. in a VSA, to approach various algorithmic problems.

VSA = Hypervector Space + Operations

In 2003, Ross Gayler established the term Vector Symbolic Architecture (VSA) for the combination of a high dimensional space and a certain set of operations with well defined properties. The set of operations includes at least:
  • ⊗ to bind hypervevtors
  • ⊕ to bundle hypervectors
An important property of these operations is that the result is again a hypervector - this allows for recursive applications of these operations. Dependent on the underlying hypervector space, the implementation of these operations is different and there are several definitions available. There is a set of properties that have to be fulfilled by the implementation of these operators. E.g., think of a bind operator which is associative and for which holds

X⊗X=I

This is, the result of binding a hypervector with itself is the identity element I. Then, the bind() operator can, e.g., be used to create role-filler pairs. Given hypervectors X and A, we can assign the value "A" to the variable "X" by using the bind operator:

H = A⊗B

To query the value of the variable X, we can apply the bind operator on the hypervector H:

X⊗H = X⊗(X⊗A) = (X⊗X)⊗A = I⊗A = A

In combination with a distributive bundle operator, we can also query a variable value from a bundle of role-filler pairs, e.g. variable hypervectors X and Y and value hypervectors A and B:

H = X⊗A ⊕ Y⊗B

Let me emphasize the fact that H is an element of the same hypervector space as variables and values. To query the value of variable X, we proceed as above, we query the result vector H with the query variable X:

X⊗H = X ⊗(X⊗A ⊕ Y⊗B) = (X ⊗X⊗A) ⊕ (X ⊗Y⊗B) = A ⊕ noise

"noise" means that the result of (X ⊗Y⊗B) is not similar of anything known (which are in this example X, Y, A, B, X⊗A, Y⊗B, and H). In fact it is very likely to be almost orthogonal to any other known vector - a result of the above listed second property of the underlying hypervector space.
To solve a task using a VSA, further elements like a clean-up memory, encoder/decoders, and further operators (e.g., a protect operator) are required. However, based on VSA, there are surprisingly elegant ways of implementing solutions to various problems: E.g. think of a algorithm for mobile robot navigation, where the sensor input, the actuator output and the whole program that maps the first to the latter, are elements from the very same hypervector space.

Learning Vector Symbolic Architectures for Reactive Robot Behaviours

VSAs can be used to model a large variety of problems. However, a major drawback of VSAs is the lack of opportunities to learn them from training data. Their power is merely an effect of good (and elaborate) design rather than learning. We exploit high- level knowledge about the structure of reactive robot problems to learn a VSA based on training data. We could obtain preliminary results on a simple navigation task: Given a successful demonstration of a navigation run by pairs of sensor input and actuator output, the system learns a single hypervector that encodes this reactive behaviour. When executing (and combining) such VSA-based behaviours, the advantages of hypervectors (i.e. the representational power and robustness to noise) are preserved. Moreover, a particular beauty of this approach is that it can learn encodings for behaviours that have exactly the same form (a hypervector) no matter how complex the sensor input or the behaviours are.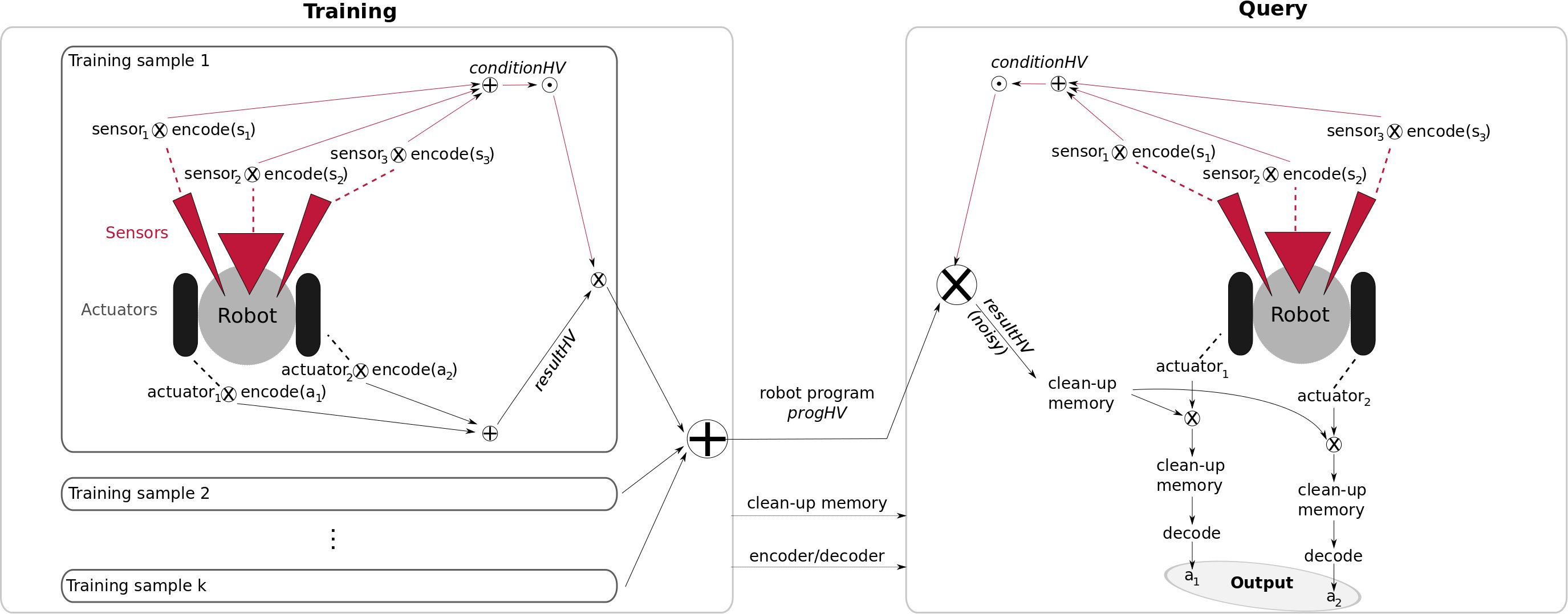

scheme.jpg

During training (left), we encode production rules in form of hypervectors and bundle them to a single hypervector, the robot program "progHV". During inference (right), the hypervector is queried with the current sensor measurements and commands for the actuators are obtained. For more details please refer to the papers below.

Software

VSA Toolbox and source code to the paper

Schlegel, K., Neubert, P. & Protzel, P. (2021) A comparison of Vector Symbolic Architectures. Artificial Intelligence Review. DOI: 10.1007/s10462-021-10110-3

can be found here: Github VSA Toolbox

For algorithm implementations that belong to particular papers, please refere to the links in the references above.