Adaptive Mixtures for Robust Factor Graph Optimization
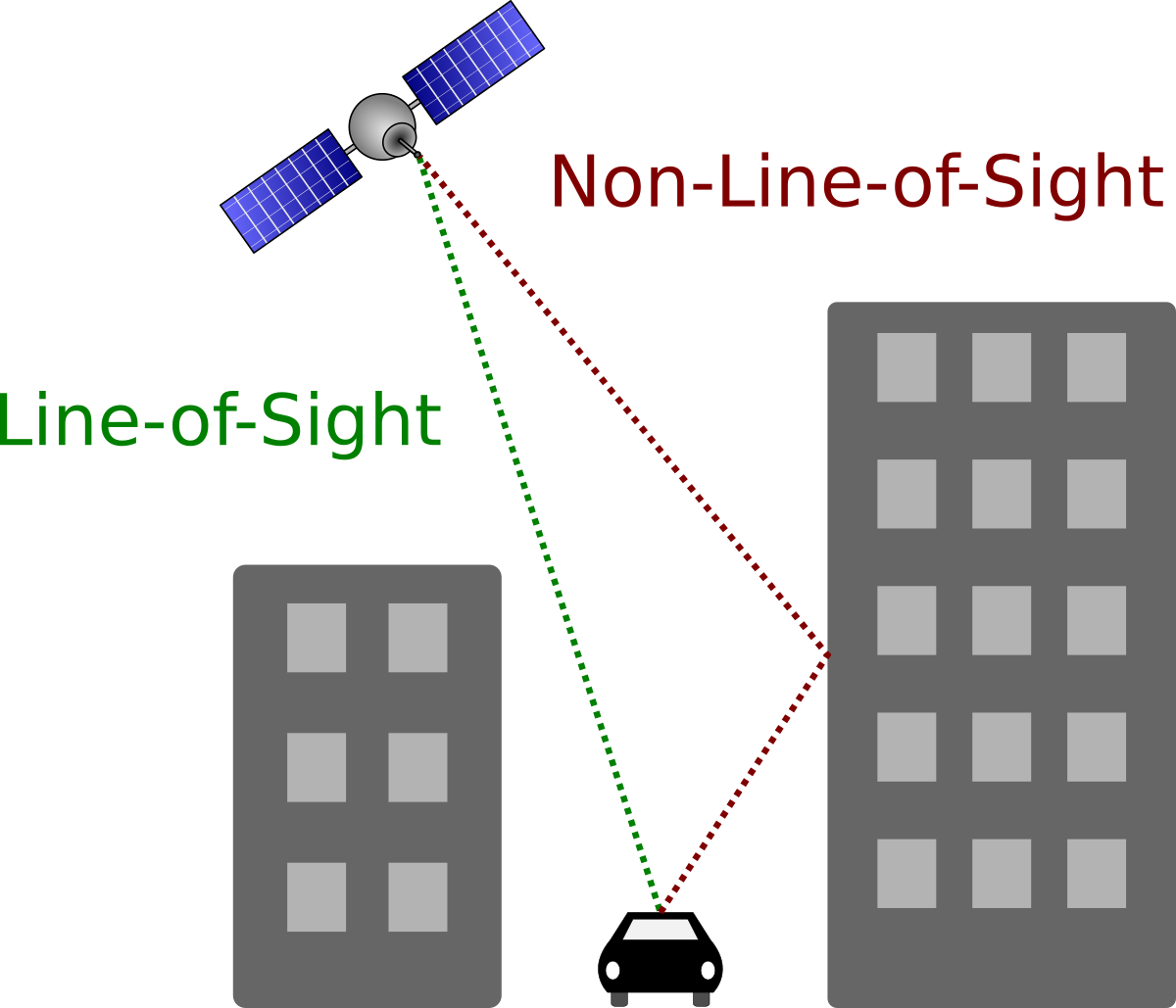
The Problem of non-Gaussian Errors
To estimate the current state of a robotic or autonomous system, almost every probabilistic sensor fusion algorithm is constructed by assuming specific error properties of one or multiple sensors. Regardless of the concrete choice of the model, a violation of model assumptions can have a strong impact on the estimation quality. Such non-Gaussian errors can have a variety of reasons. Wheel odometry can slip and return too high values and ultrasonic range finders or radar can measure signals that are reflected from multiple surfaces. Radio-based ranging like distance measurements or satellite-based localization can suffer from non-line-of-sight (NLOS) Effect. One example is shown on the right, where the NLOS reflection causes a multimodal Sum-of-Gaussian distribution. More Information: NLOS in GNSS systems
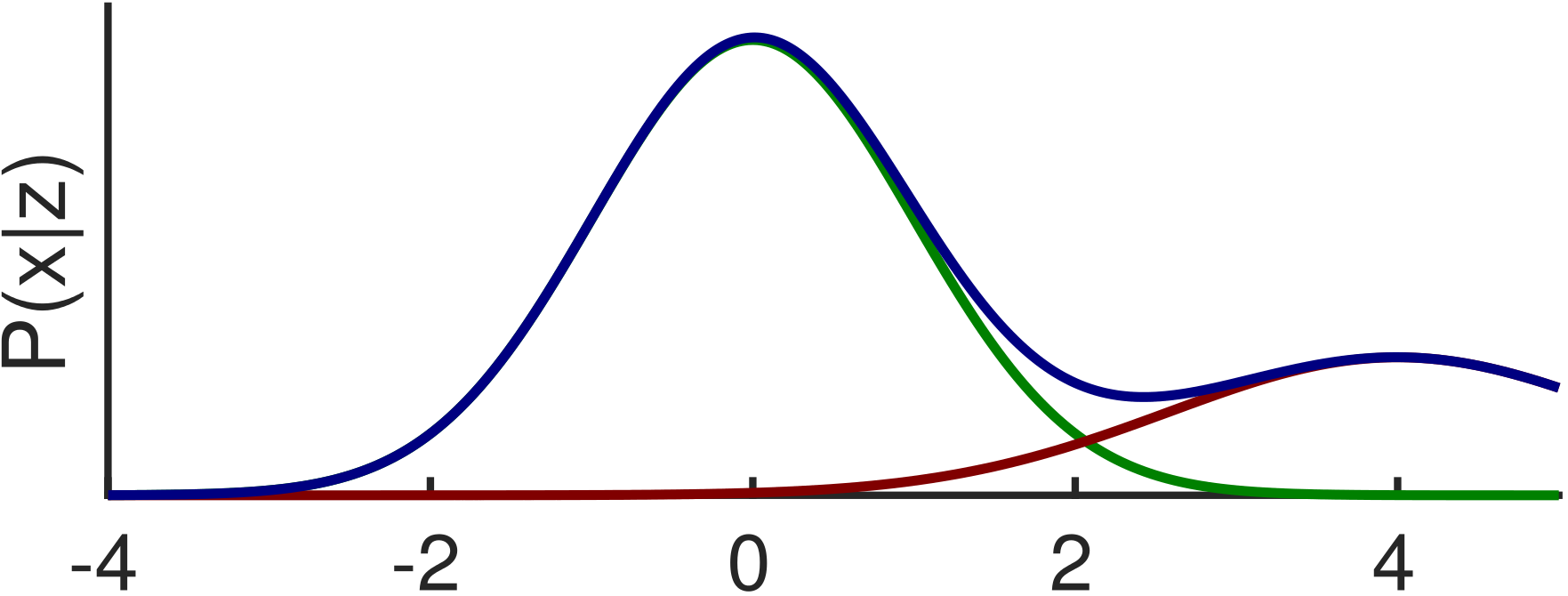
Since the resulting distributions are asymmetric or heavy-tailed, algorithms like Kalman filters or factor graphs are not able to estimate the systems state in a reliable way. Instead the estimation result will be strongly biased. There already exist approaches to use non-Gaussian distributions in factor graphs. However, their common problem is the lack of concepts to parameterize this distributions without prior knowledge that is often not available.
Adaptive Mixtures and the EM Algorithm
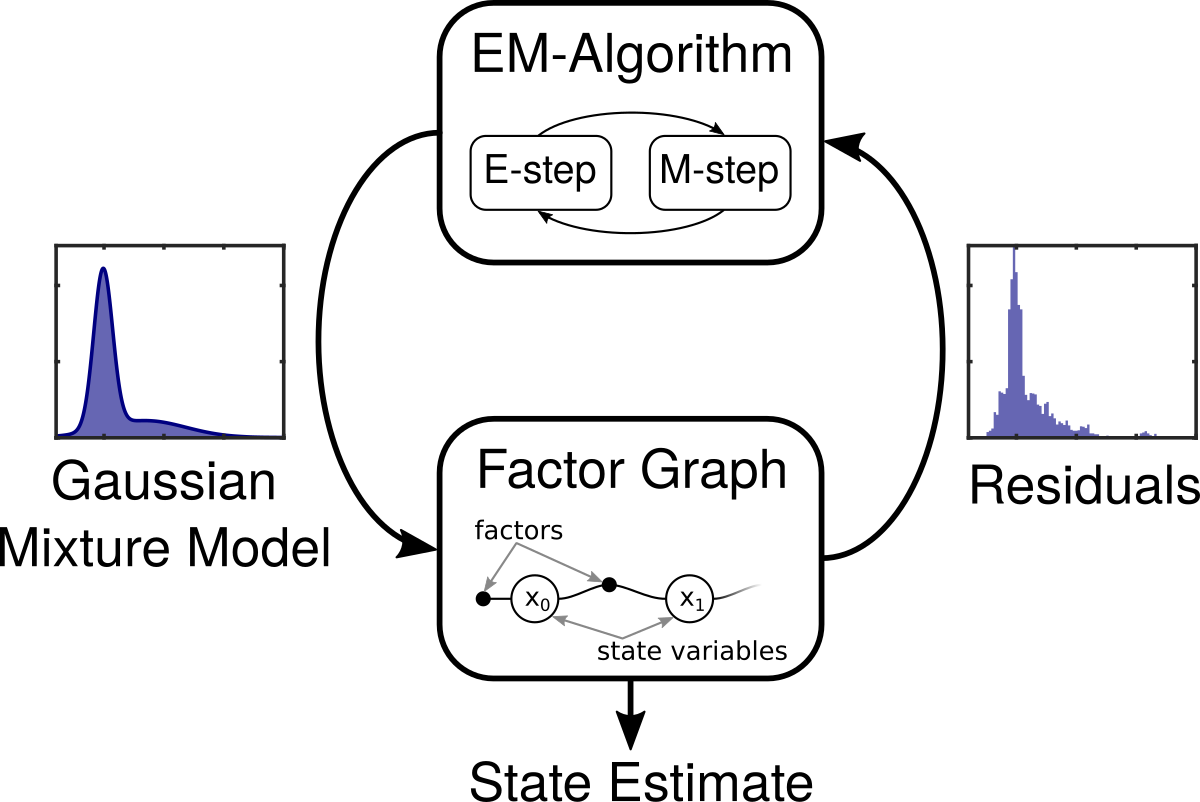
To overcome the problem, we proposed the idea of Adaptive Gaussian mixture models (GMM), where a multimodal GMM is used to describe the measurement errors. In difference to the previously published Self-tuning Mixture approach is the estimation process of the error model and the state of the system separated in two alternating steps. As the picture on the right shows is a Expectation-Maximization (EM) algorithm applied to adapt the GMM to the residuals of the factor graph. This leads to well-behaved convergence properties and as much easier initial parametrization of the GMM, compared to Self-tuning Mixture.
The evaluation on several localization datasets showed how the dynamic estimation of the error model can improve the overall estimation quality. All datasets are available online on this page. The source code is also published as part of the robust sensor fusion library libRSF on GitHub .
Download Datasets
Chemnitz City GNSS Dataset (14 MB)
Publications
- (2019) Expectation-Maximization for Adaptive Mixture Models in Graph Optimization. In Proc. of Intl. Conf. on Robotics and Automation (ICRA). DOI: 10.1109/ICRA.2019.8793601
