Research
My research focus lies at the interface of geometric analysis, low-dimensional topology, harmonic analysis, and numerics.
A long-term project focuses on the analysis and discretization of curvature energies that measure geometric properties of embedded curves and surfaces. In particular, these energies reveal information about isotopy types. Technical difficulties arise from the nonlinear and nonlocal nature of the corresponding PDEs.
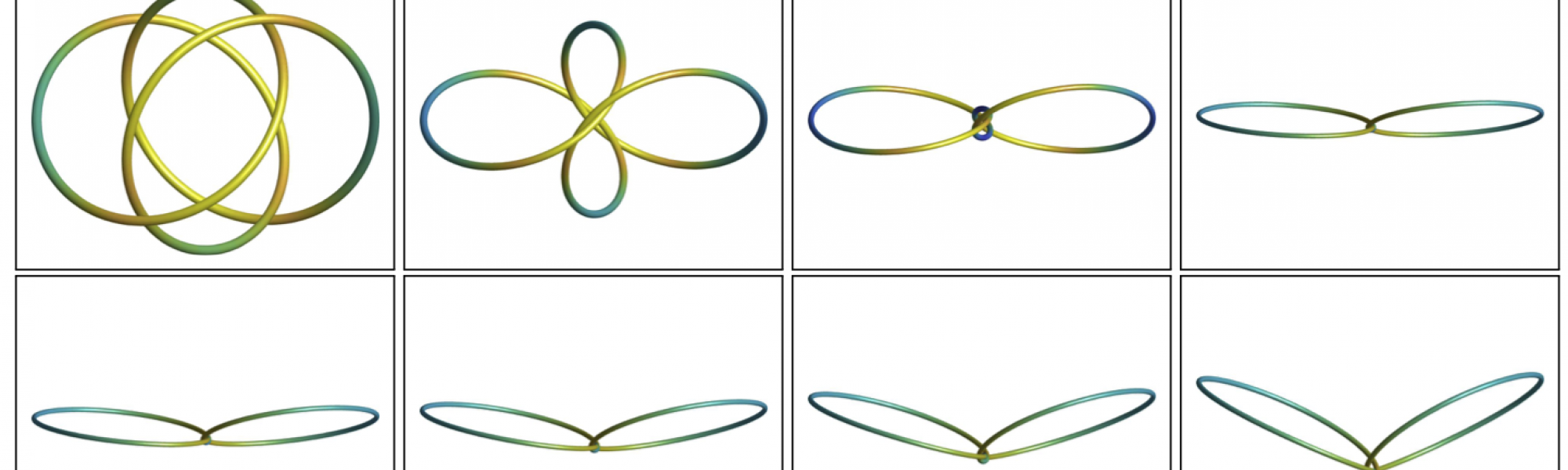
Curvature energies can be employed to model steric constraints. For instance, one can find minimizers of the elastic energy within a given isotopy class by a regularization approach involving a self-avoiding functional. It is a challenging project to determine the shape of limit configurations of these minimizers, e.g., elastic knots.
Geometric curvature energies have originated from the search of „nicely“ embedded objects within a given isotopy class. An important example is the field of knot energies that has emerged during the past thirty years. Several families of knot energies that have been proposed so far raise analytically intricate questions.
Another project concerns the study of anisotropic energies where distinct space directions are weighted differently. Regularizing a non-convex anisotropy with a suitable higher-order functional leads to a phase transition problem whose evolution exhibits interesting phenomena.