Arbeitsgruppe: "Ungeordnete Quantensysteme"

Der Übergang eines Materials vom metallischen in den isolierenden Zustand ist ein bis heute nur unvollständig verstandenes Phänomen. In den letzten Jahrzehnten sind im wesentlichen zwei verschiedene Mechanismen untersucht worden: Zum einen kann ein solcher Metall-Isolator Übergang (engl: Metal-Insulator-Transition MIT) durch eine Vielteilchwechselwirkung (Mott-Übergang), zum anderen durch Unordnung (Anderson-Übergang) induziert werden.

Im Anderson Modell bewegen sich unkorrelierte Elektronen auf einem regelmäßigen Gitter, wobei aber die potentiellen Energien an den Gitterplätzen zufällig gewählt werden. Dies führt zu einer Lokalisierung der Einteichenwellenfunktionen für genügend starke Unordnung und damit zu einem Isolator. Bei schwacher Unordnung sind die Eigenfunktionen räumlich ausgedehnt ähnlich den Blochwellen in einem idealen Kristall. Zur Bestimmung der Phasengrenze zwischen Metall und Isolator im Energie-Unordnungsdiagramm und zur Berechnung der den Übergang charakterisierenden kritischen Exponenten hat sich der Transfermatrix-Algorithmus zusammen mit der Technik des Finite-Size Scaling als nützlich erwiesen.

Mit diesen Methoden betrachten wir auch dreidimensionale Systeme mit anisotroper Nächste-Nachbar Wechselwirkung. Insbesondere wird die Leitfahigkeit einer solchen anisotropen Probe im Rahmen des Kubo Formalismus berechnet und als Funktion von Unordnung und Anisotropie untersucht.

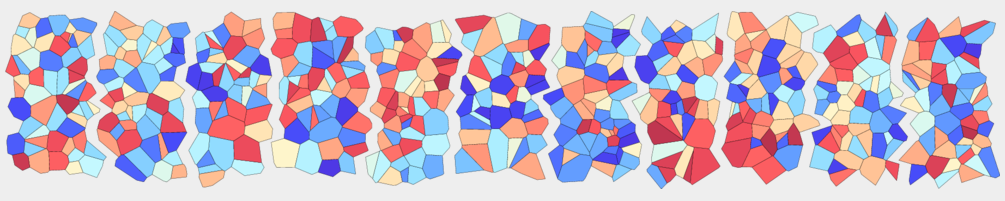
Eine Möglichkeit zur Charakterisierung des Anderson-Übergangs besteht in der direkten Untersuchung der Wellenfunktionen. Aufgrund der Unordnung sind diese Eigenfunktionen allerdings nicht analytisch berechenbar. Sie werden deshalb numerisch durch Diagonalisierung des Hamiltonoperators bestimmt. Mit Hilfe von Algorithmen, welche auf dünn besetzten Matrizen aufbauen, können Systeme in der Größenordnung von Millionen Gitterplätzen betrachtet werden. Die bei der Annäherung an den Phasenübergang divergierende Korrelationslänge legt die Vermutung nahe, dass die Wellenfunktionen bei der kritischen Unordnung fraktales Verhalten zeigen, da dort keine charakteristischen Längenskalen existieren. Eine detailliertere Analyse dreidimensionaler Systeme ergibt, dass die Wellenfunktionen dort als Multifraktale beschrieben werden können.

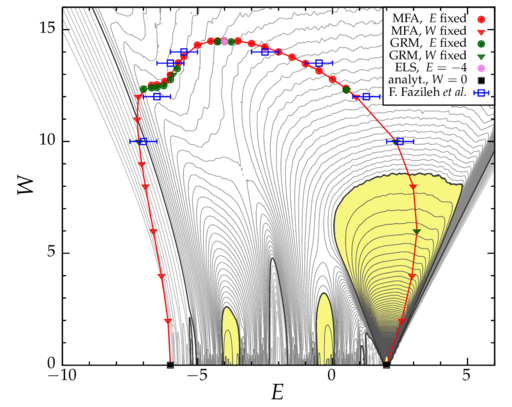
Anstatt der Eigenfunktionen können auch die Energieeigenwerte bzw. deren statistischen Eigenschaften genutzt werden, um den Anderson-Übergang zu charakterisieren. Speziell untersuchen wir Abstandsverteilungen der Eigenwerte und nutzen Finite-Size-Scaling um den kritischen Exponenten zu bestimmen.

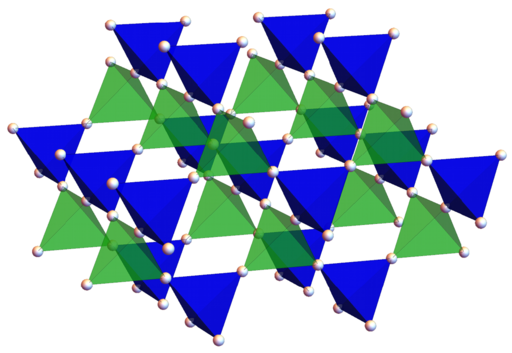
Beide Charakterisierungsmethoden werden auf Hamiltonmatrizen angewendet, welche die Verknüpfung des eckenteilenden tetragonalen Gitters beschreiben. Dieses spezielle Gitter tritt in der Natur als Untergitter, z.B. in der Spinell-Struktur, auf. Die Struktur lässt sich mit dem fcc-Bravais-Gitter und einer 4-atomigen Basis beschreiben. Die Verknüpfungen zwischen den Basisatomen bilden einen Tetraeder. Die Verknüpfungen von Basisatomen zwischen benachbarten Einheitszellen kann ebenfalls durch Tetraeder beschrieben werden. Beide Tetraeder teilen sich die Eckpunkte und sind inversionssymmetrisch zueinander. Diese Konstruktion hat an jedem Gitterplatz 6 nächste Nachbarn.

Publikationen

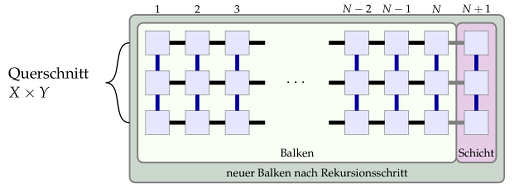
Eine weitere Möglichkeit der Charakterisierung führt über die Berechnung der Lokaliserungslänge. Hierfür wird die exponentiell abklingende Transmission durch einen quasi eindimensionalen Balkens unter Verwendung eines iterativen Green-Funktions-Formalismus berechnet. Diese Methode hat gegenüber dem Transfermatrix-Algorithmus den Vorteile, dass nicht jeder Gitterplatz einer Schicht mit dem einer benachbarten verknüpft sein muss. Unter Verwendung von verschiedenen Balkenquerschnitten (Finite-Size-Scaling) ist es möglich den Phasenübergang und kritischen Exponenten zu bestimmen, welche mit denen aus der Multifraktalanalyse und der Energieniveaustatistik übereinstimmen sollten.

Publikationen

Das zufällige Voronoi-Delaunay Gitter ist ein topologisch ungeordnetes Gitter. Es beschreibt u.a. amorphe Materialien, Schwämme und Gewebe. Dies wird aus zufällig gewählten Atompositionen mit Hilfe der Delaunay-Dreieckszerlegung eindeutig gebildet. Die Kanten der Dreiecke spiegeln die Verknüpfungen wider. Die Anzahl der Verknüpfungen hängt so von der Position ab. Das Voronoi-Diagramm ist eine zur Delaunay-Dreieckszerlegung duale Darstellung . Aufgrund des restriktiven Aufbaus kommt es zu räumlichen Korrelationen zwischen verschiedenen charakteristischen Merkmalen des Gitters. Dieses topologisch ungeordnete Gitter kann in beliebigen Dimensionen gebildet werden, wobei der zwei- und dreidimensionale Fall von besonderer Bedeutung sind.

In diesem topologisch ungeordnetem System wird das Verhalten von Elektronen mit und ohne Einfluss eines äußeren magnetischen Feldes untersucht und charakterisiert. Dafür wird die Multifraktalanalyse in Kombination mit dem Finite-Size-Scaling verwendet. Von besonderem Interesse ist es, inwieweit Phasenübergänge auftreten und die Frage, welche Auswirkungen die topologische Unordnung auf das qualitative Verhalten der Elektronen hat.

Kooperationen

Publikationen

Kooperationen