Die Geometrie gerahmter Kurven
Themenvorschlag zum Computerpraktikum im Winter 2020/21
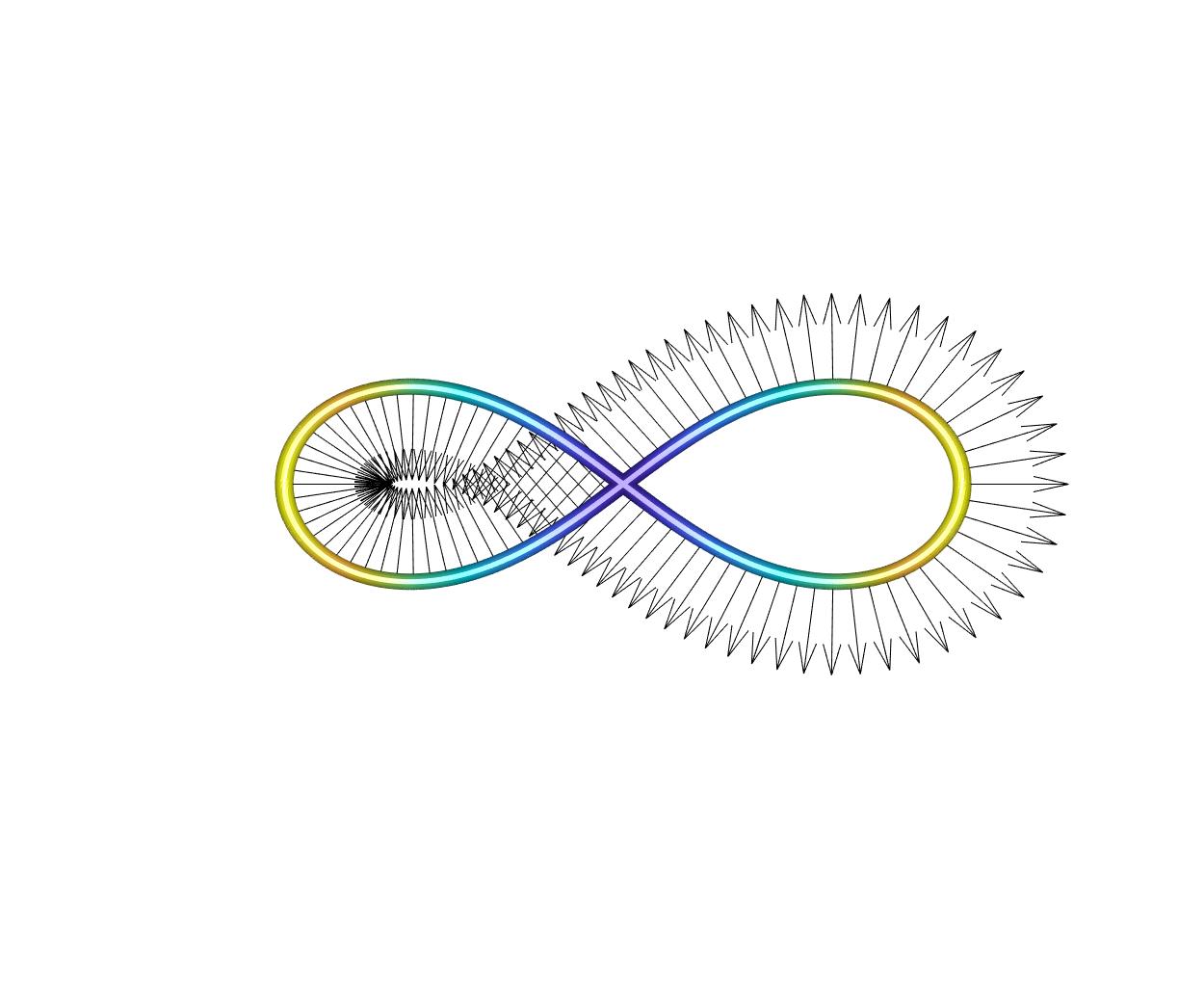
Zu einer geschlossenen glatten Kurve \(\gamma:[0,L]\to\mathbb R^3\) betrachten wir Rahmen, d. h. Normalenfelder \(a:[0,L]\to\mathbb S^2\) mit \(a\perp\gamma'\). In nebenstehender Abbildung ist ein Normalenfeld durch Pfeile visualisiert. Wir setzen im Folgenden Bogenlängenparametrisierung voraus, also \(|\gamma'|=1\). Ein Beispiel stellt der Frénet-Rahmen \(a_F= \left.{\gamma''}\Big/{|\gamma''|}\right.\) dar.
Für praktische Zwecke betrachtet man natürliche Rahmen \(a_\circ\), die durch die Bedingung \(\det(\gamma',a_\circ,a_\circ')=0\) charakterisiert sind.
Einen besonderen Fall erhält man für geschlossene Kurven mit geschlossenen Normalenfeldern, d. h., \(\gamma\) und \(a\) sind periodische Funktionen auf \(\mathbb R\). In diesem Fall ist \(\tilde\gamma=\gamma+\varepsilon a\) für geeignete \(\varepsilon>0\) eine geschlossene Kurve, die keine gemeinsamen Punkte mit \(\gamma\) hat. Die Verschlingungszahl dieser beiden Kurven berechnet sich nach der bekannten Formel \[ \mathrm{Lk}(\gamma,\tilde\gamma) = \tfrac1{4\pi}\iint \frac{\det\left(\gamma(x)-\tilde\gamma(\tilde x),\gamma'(x),\tilde\gamma'(\tilde x)\right)}{|\gamma(x)-\tilde\gamma(\tilde x)|^3}\, \mathrm d x \, \mathrm d \tilde x, \] die auf Gauß zurückgeht. Sie ist eine topologische Invariante, denn ihr Wert ist stets ganzzahlig und ändert sich nicht bei kleinen Deformationen. Tatsächlich lässt sie sich als Abbildungsgrad charakterisieren.
Die Verschlingungszahl tritt insofern in der algebraischen Topologie, der nichtlinearen Analysis und einigen Anwendungen im Bereich der Quantenmechanik, des Elektromagnetismus und der Molekularbiologie auf. Die Singularität im Nenner des Integranden muss bei der Diskretisierung angemessen berücksichtigt werden.
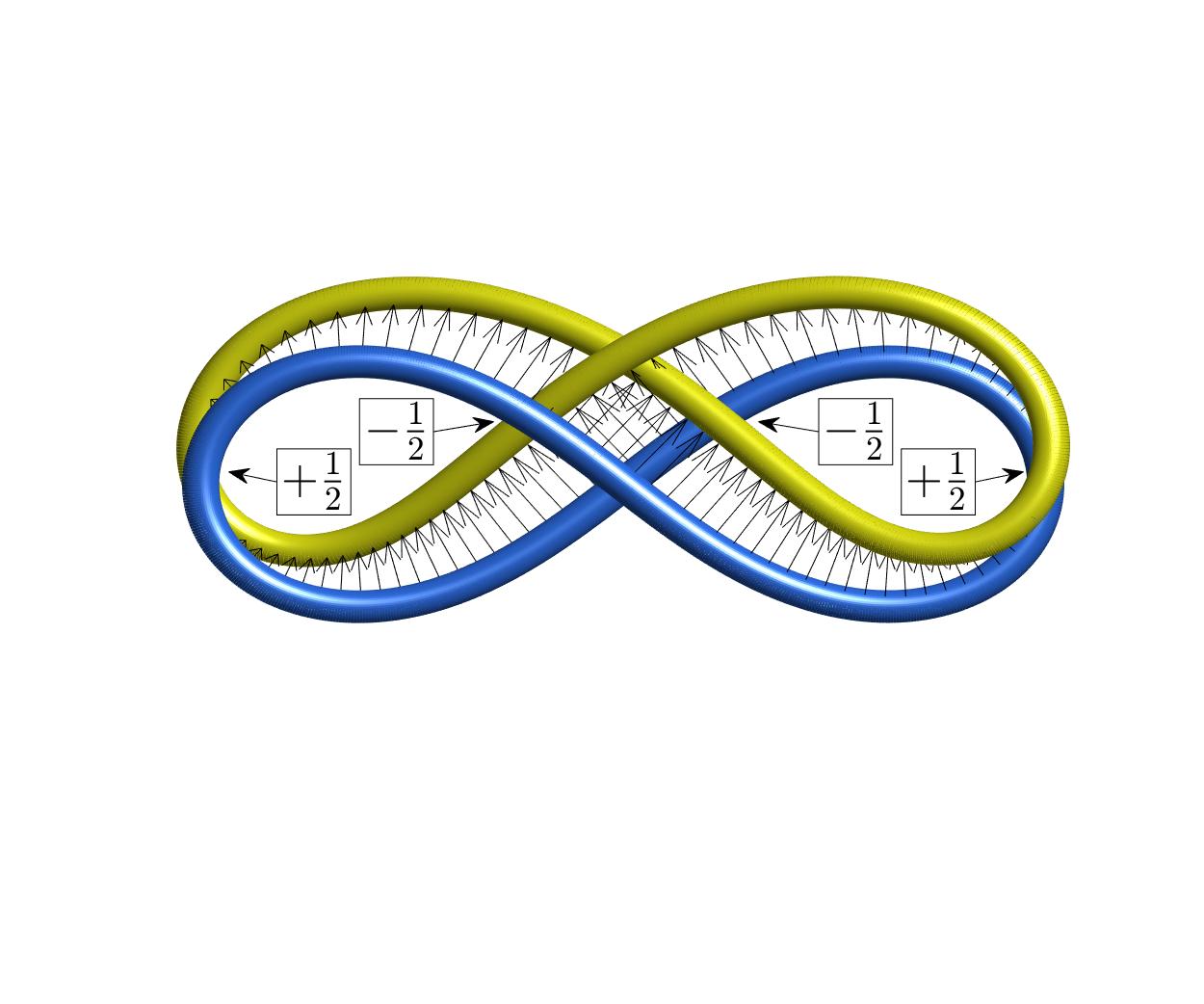
In diesem Zusammenhang ist es interessant, dass man die Verschlingungszahl auch als Summe der signierten Überkreuzungen der beiden Kurven berechnen kann, wobei die gewählte Projektionsrichtung (fast) unerheblich ist. In nebenstehendem Beispiel beträgt die Verschlingungszahl null, und hier kann man die beiden Kurven tatsächlich voneinander separieren (was aber nicht immer der Fall ist).
Bei Betrachtung der Überkreuzungen wird deutlich, dass sie entweder lokal (die beiden äußeren) oder global (die beiden mittleren) sind. Dies nun führt auf zwei neue Funktionale, Writhe und Twist, deren Summe stets die Verschlingungszahl ist (Satz von Călugăreanu). Im Gegensatz zu dieser sind jene keine topologischen Invarianten; sie hängen erheblich von der Geometrie der Kurve bzw. des Rahmens ab.
Im Praktikum sollen zunächst Kurven und Rahmen berechnet und dargestellt werden. Anschließend werden Diskretisierungen der oben vorgestellten Funktionale implementiert. Nachdem der Code anhand einiger Beispiele getestet worden ist, können weitere Experimente im Kontext gerahmter Kurven durchgeführt werden. Da Visualisierung eine maßgebliche Rolle spielt, ist die Programmierumgebung Matlab bzw. Octave besonders geeignet.
| Dozent | Philipp Reiter, Raum C46.719, +49 371 531…, philipp.reiter@… Sprechstunde nach Vereinbarung |
|---|---|
| Bitte beachten Sie auch die weiteren Hinweise zum Computerpraktikum. | |
| Aufbauend auf das Praktikum kann eine Bachelorarbeit vergeben werden. |