Compliant mechanisms
Design methods for compliant mechanisms
 |
"The development of new materials and design methods is the key to unlocking the potential of compliant mechanisms. These mechanisms will bring about a paradigm shift in the design of technical products." - Prof. Dr. sc. ETH Alexander Hasse |
1 Compliant vs. conventional mechanisms; advantages and disadvantages
As mechanisms, the nutcracker and the tweezers are designed according to two different principles. In the first case, the function of the mechanism is enabled by the inclusion of a pin joint between two rigid elements. In the second case, the elasticity of certain areas of the structure provides the necessary pivoting. This makes the difference between conventional and compliant mechanisms: The nutcracker is a mechanism of the conventional type, while the tweezers are a compliant mechanism.
Many of the advantages of compliant systems are obvious: They are free of backlash, wear and friction. They basically require no lubrication. They can be manufactured in one piece, without complex assembly procedures. They are easier to clean due to the absence of gaps and other discontinuities on the surface. They do not release particles due to the lack of wear. They can be used freely in heavily polluted environments and are also quieter. Another set of advantages results from specific analyses: compliant mechanisms are more precise,easier to miniaturize and lightweight.
The disadvantages of compliant mechanisms include a fundamental limitation on deformation due to limited allowable strain. In addition, the design of compliant mechanisms is much more complex for reasons explained below.
2 What is our research focus in the area of compliant mechanisms?
Despite the numerous advantages of compliant mechanisms, mechanical engineering is dominated by conventional mechanisms. One of the reasons of this is the above mentioned much higher complexity of the design of compliant mechanisms compared to conventional ones. The staff of our institute, which deals with compliant mechanisms, has partly decades of experience with the topic of their design and continuously develops this focus in targeted research work.
The design of conventional mechanisms benefits from an important fact: Their desired deformations result from relative rigid-body motions of the links to each other. Therefore, they can basically be analyzed without considering forces and elastic deformations. In design, the determination of the desired deformations is a purely topological-geometric task. Only in a subsequent phase are the individual elements (links and joints) dimensioned. The kinematic aspect (i.e. the consideration of the desired, functional deformations) can therefore be completely separated from the static aspect (the consideration of forces and resulting stresses in the material). This is not possible with compliant mechanisms. A compliant system modeled without considering elastic strains would not be able to represent a desired deformation. Thus, the relationship between force and deformation must be considered from the first step in the design of compliant mechanisms. In addition, requirement conflicts between deformability and load capacity are much less problematic to resolve in conventional mechanisms because these properties are assigned to separate components: Links and joints can be stiffened as desired without negatively affecting the kinematics (i.e., the feasibility of realizing the desired deformations). In compliant systems, deformability and loadability must be balanced at every point in the system: If a cross-section is strengthened, this will have a positive effect on load-bearing capacity on the one hand, and a negative effect on deformability on the other. For this reason, the design of compliant systems above a certain complexity is always carried out on the basis of a formally imposed optimization task.
An optimization task consists of different subtasks, for which different special knowledge is required. First (parametrization), in order to mathematically capture the object of the design (given constant material, the unknown geometry of the mechanism) must be parametrized so that it can be expressed as a function of a certain number of variables (design variables). Second (problem formulation), it must be defined which mathematical function of the design variables (objective function) should be minimized or maximized and under which constraints (restrictions) this should be done. And thirdly (search strategy) the algorithm must be selected, by which the optimal solution is to be found.
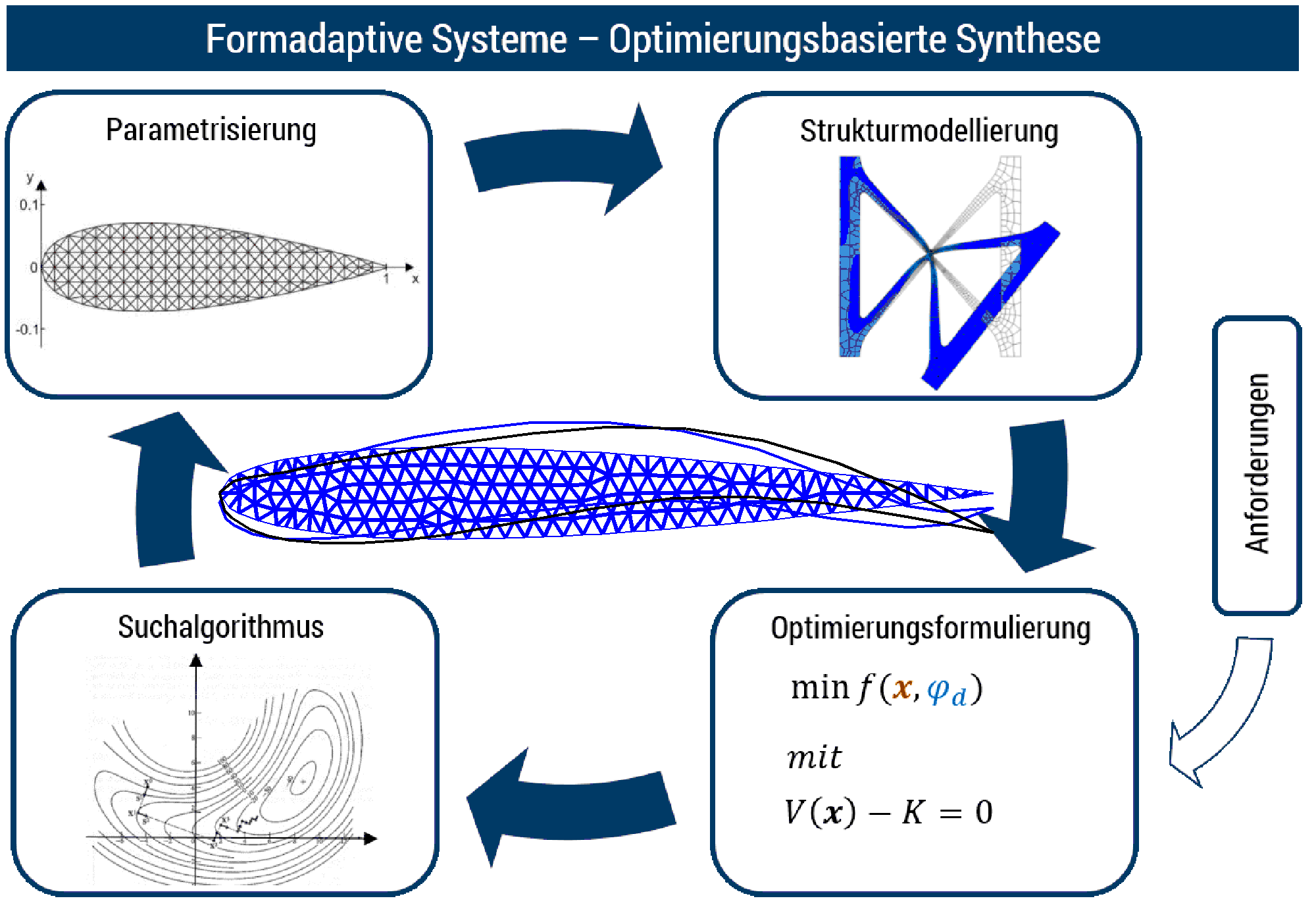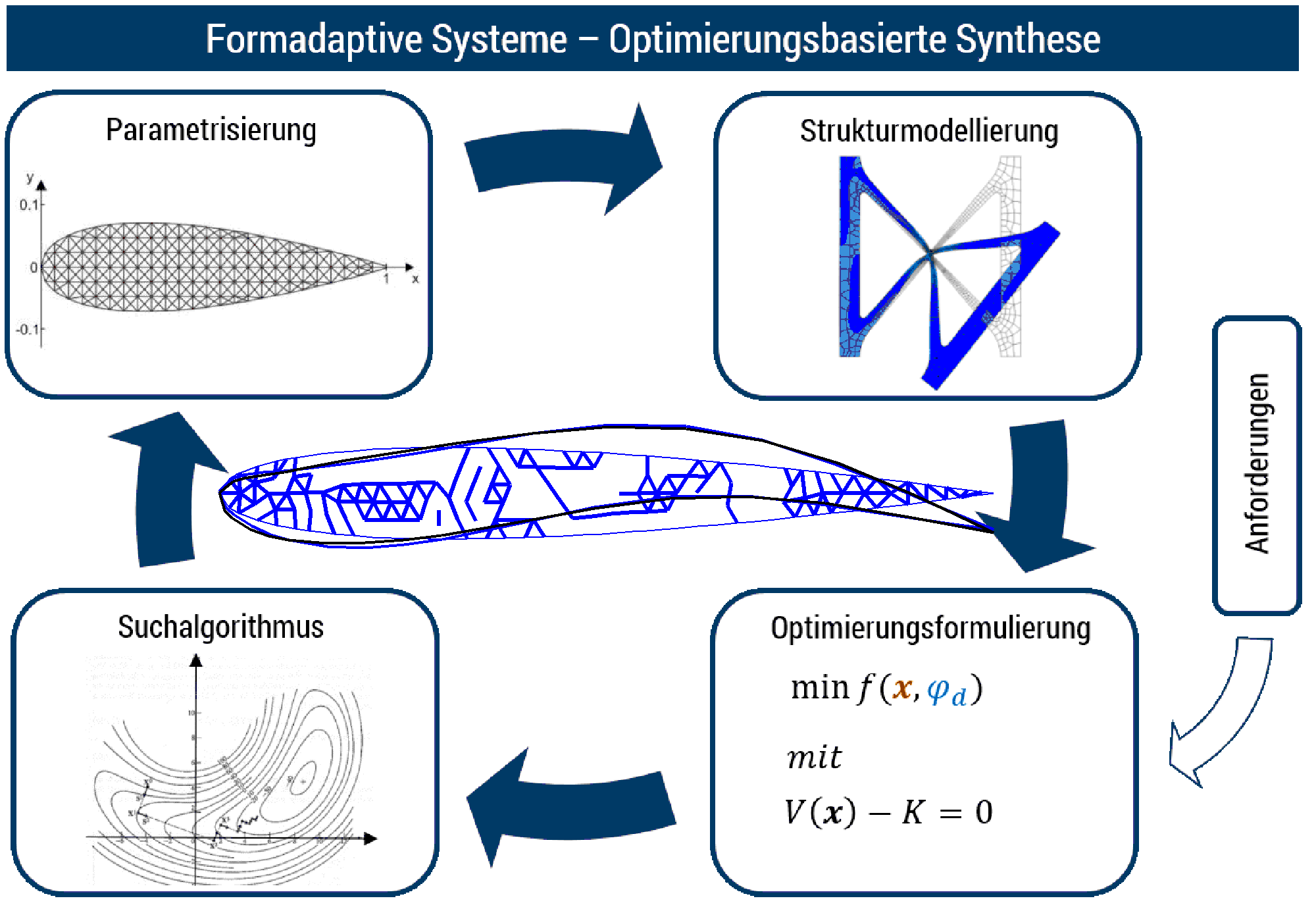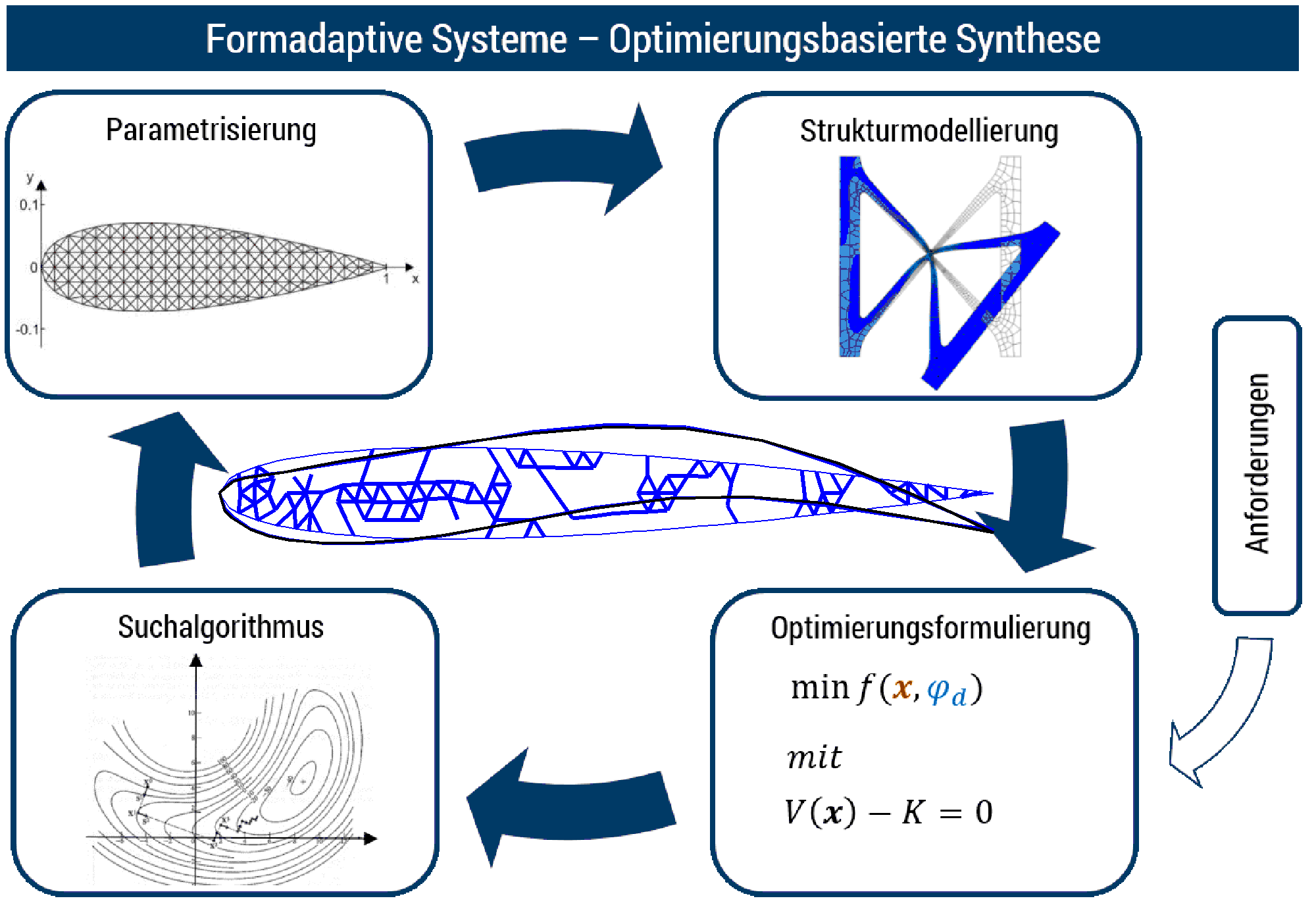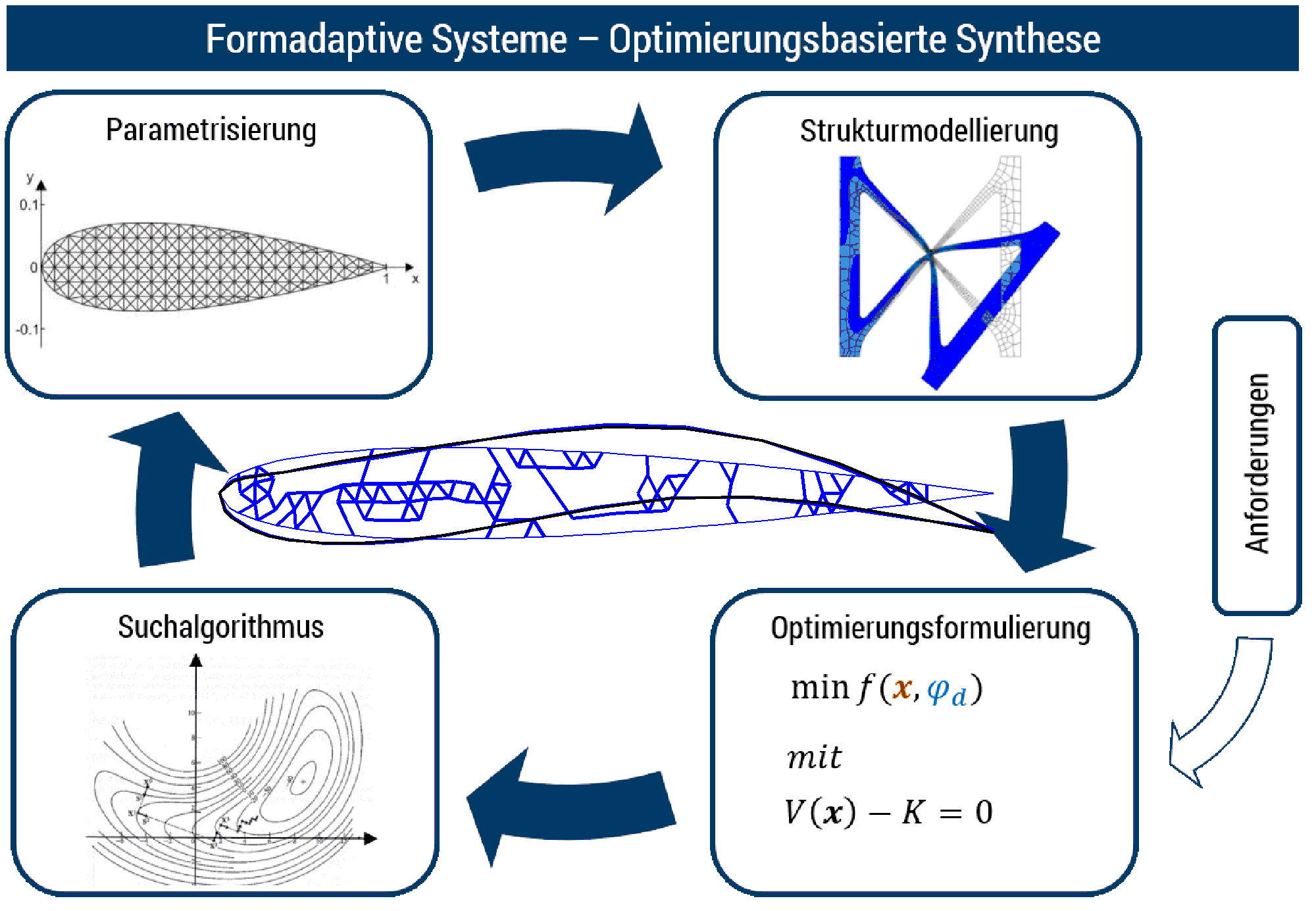 As far as our research in the field of design of compliant mechanisms is concerned, the main focus is on the study of suitable problem formulations. As far as parameterization is concerned, we specialize in the so-called topology optimization, where the domain in which the geometry is to be defined is partitioned into a fine mesh of elements. The contribution of each element to the stiffness of the system is scaled by a factor (density). The densities of the individual elements then represent the design variables. A special topic addressed at the institute in this context is the integrated design of compliant mechanisms and actuators that provide for the activation of the mechanisms.
As far as our research in the field of design of compliant mechanisms is concerned, the main focus is on the study of suitable problem formulations. As far as parameterization is concerned, we specialize in the so-called topology optimization, where the domain in which the geometry is to be defined is partitioned into a fine mesh of elements. The contribution of each element to the stiffness of the system is scaled by a factor (density). The densities of the individual elements then represent the design variables. A special topic addressed at the institute in this context is the integrated design of compliant mechanisms and actuators that provide for the activation of the mechanisms.
3 What are pseudo-kinematic design approaches?
In the context of the problem formulation issue, we succeeded in setting a milestone with the modal procedure, which is the first example of so-called pseudo-kinematic approaches.
It was mentioned above that a strict separation between kinematics and statics is not possible in the design of compliant systems. This has led the scientific community to completely give up the claim of a kinematic design and to design methods basically load case oriented. That is, a limited number of load cases are considered in the problem formulation and the response of the system to deviating load cases is not considered. In our work, on the other hand, we have looked for ways to maintain the kinematic requirement in the design as much as possible, and to optimize the geometry of the system for tending to respond with strongly similar deformations for a very wide range of load cases. We have called this property (small differences in deformation for pronounced differences in load) selectivity. We basically made high selectivity the main goal of optimization, and then focused on giving the selectivity a mathematical equivalent to translate the maximization of selectivity into appropriate problem formulations. We call this approach pseudo-kinematic.
In conventional mechanisms (as long as they are idealized as systems of rigid bodies and perfect joints), selectivity is given in the absolute sense, because there exists an infinite number of loads that lead to exactly the same deformation. In the case of compliant mechanisms, on the other hand, selectivity is a quantitative variable, since, as mentioned, each deformation is coupled with a very specific load, and thus it is not possible for two different loads to lead to the same deformation. If we deepen this fact mathematically in the simple case of linear systems, we come to the basis of the modal procedure.
Let us first consider a plane conventional mechanism at small deformations. The mechanism is modeled using the finite element method, where the links are no longer considered ideally rigid, but are assigned finite stiffness. One of the links is clamped firmly. The FE method then provides the relationship between displacements and forces in the form of a system of linear equations. Since we have a mechanism, the coefficient matrix of the displacements (the stiffness matrix) is singular. This implies that the system has either no solution at all, or infinitely many solutions. Thus, the unique coupling between load and deformation discussed above cannot exist: Most loads do not lead to a solution, and again there are solutions that are feasible with different loads. If we again model a compliant mechanism in a similar way, the coupling mentioned above is given. The stiffness matrix is regular, and the system is always invertible. For any given load there is a single static solution and vice versa. However, it will happen that with different loads very similar deformations are to be realized. This property (the selectivity) is found in the so-called condition of the stiffness matrix, which in turn is related to the eigenvalues of the stiffness matrix. For singular matrices, at least one eigenvalue is zero. The number of vanishing eigenvalues of a singular matrix is called the rank decay R of the matrix and quantifies the number of rows of the matrix that can be expressed as a linear combination of the others. For solutions to exist, the same ratios must also hold on the right-hand side of the equations, so that R whole equations can be expressed as linear combinations of other equations. It is obvious that a stiffness matrix with an eigenvalue that is very small with respect to the others (ill-conditioned matrix) behaves approximately like a singular matrix. Strictly speaking, there will be different solutions for each imposed load, but they will have approximately the same ratio between the individual displacements. This ratio is given by the eigenvector associated with the very small eigenvalue.
If the design succeeds in influencing the stiffness matrix in such a way that one eigenvalue is small in relation to the others and that the corresponding eigenvector maps the desired deformation, the design of the system is methodically brought close to the kinematic design of conventional systems, since a certain deformation is impressed on the system as the preferred deformation, independent of the load case.
This is the modal procedure, which by its nature is only valid for linear systems in this form. It has been gradually developed with respect to the concrete formulation as well as with respect to algorithmic aspects since the first formulation from 2008 and is currently used as the basis of a more general, pseudo-kinematic procedure, which also applies to nonlinear systems.
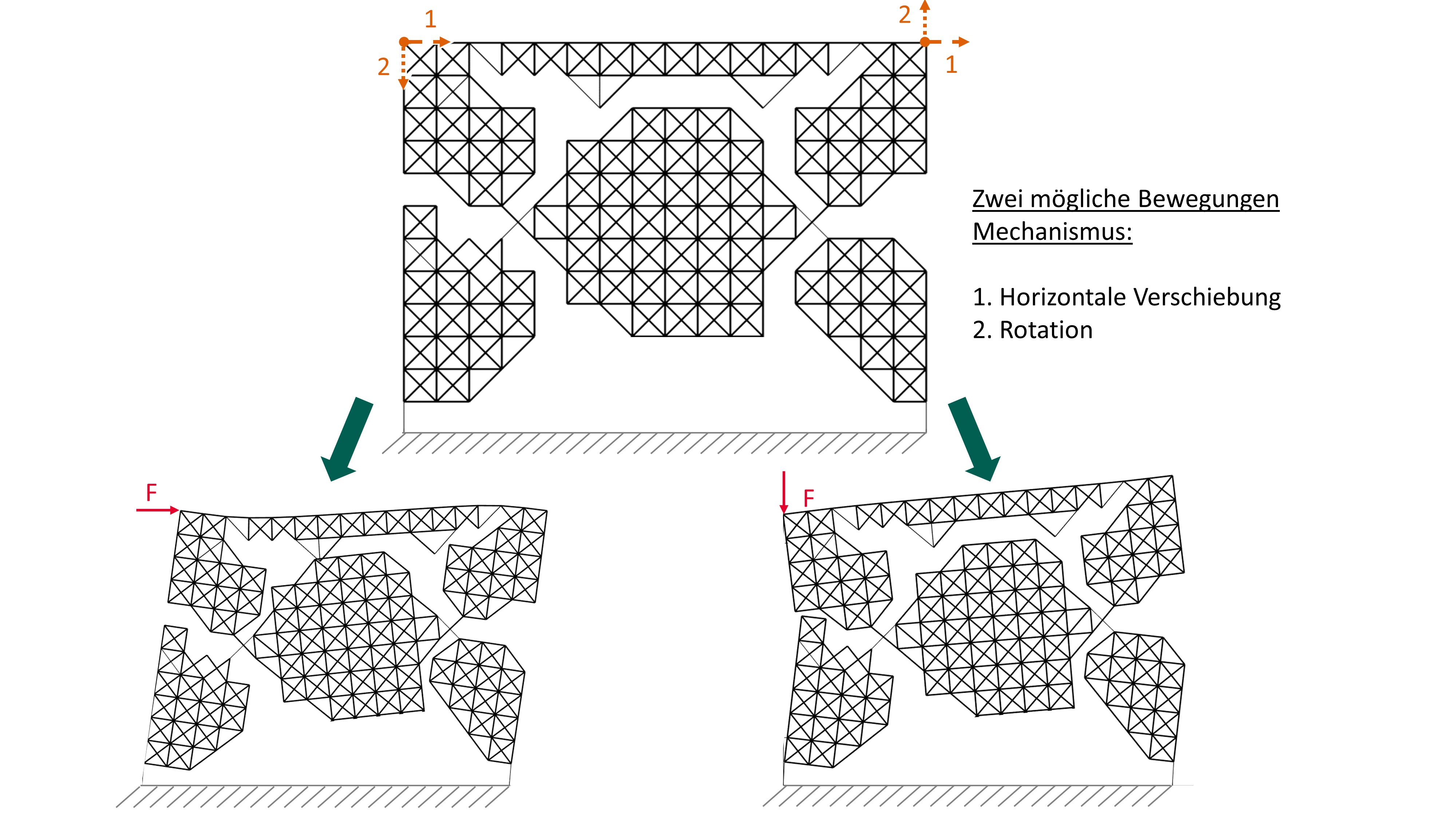
Apart from the load case independence, the modal procedure also represents a quantum leap forward in the research on the design of compliant mechanisms due to its application flexibility. It can be applied without extensive formulation changes to systems with kinematics defined over a large number of degrees of freedom, as well as to so-called compliant mechanisms with multiple pseudo-mobility. Compliant mechanisms with multiple pseudo-mobility are the compliant equivalent of conventional mechanisms with multiple mobility, i.e., mechanisms that have more than one degree of freedom when represented as systems of rigid bodies and ideal joints.
4 Publications
5 MATLAB design procedures
| Paper title | First author | Link professorship page | Link Mendely Data |
| Synthesis of compliant mechanisms with selective compliance - An advanced procedure | Kirmse | www.tu-chemnitz.de/mb/mp/mmt | https://data.mendeley.com/datasets/697dnbtz62/2 |
| How to prestress compliant mechanisms for a targeted stiffness adjustment | Mauser | www.tu-chemnitz.de/mb/mp/sms | - |
| Topology-optimization based design of multi-degree-of-freedom compliant mechanisms (mechanisms with multiple pseudo-mobility) | Seltmann | www.tu-chemnitz.de/mb/mp/jimss | https://data.mendeley.com/datasets/c5k9xnyvtb/1 |
| Topology optimization of compliant mechanisms with distributed compliance (hinge-free compliant mechanisms) by using stiffness and adaptive volume constraints instead of stress constraints | Seltmann | www.tu-chemnitz.de/mb/mp/mmt22 | https://data.mendeley.com/datasets/wzzdvf8nts/2 |
6 Research projects
Coupled design of selectively compliant mechanisms and actuators
| Funding agency: | DFG |
| Research association: | |
| Duration: | 24 Months |
| Start time: | Jan 2021 |
| Editor: | Alexander Nowak |
| Further Information: | DFG-Projekt |

Active mechanical systems consist of a passive mechanical system (mechanism) and an actuator system. This proposal focuses on a special case scenario, whereby the mechanical system is a compliant mechanism. Compliant mechanisms perform the function of conventional mechanisms but in principle, they do not have any movable components (bearings, guides or joints). Instead, their functions rely on the targeted deformation of flexible regions.
As a rule, compliant systems are designed on the basis of an optimization task. There are numerous factors that show the benefits of extending this kind of methodology to the design of the accompanying actuator system:
1) The flexible regions of compliant systems are only capable of bearing concentrated forces to a limited extent. An analysis of local deformations or of the excitation of undesired deformation components must be performed when designing the actuator system, which can be only performed at reasonable expenses within the scope of a formal optimization.
2) Compliant systems offer (and in some cases even require) the option of distributed activation. The design of a distributed actuator system is too complex to be undertaken successfully without the help of a formal optimization procedure.
3) Synergies can be exploited by coupling the designs of mechanism and actuator system. In particular, it is possible to integrate the load-bearing properties of the actuators into the mechanical design (especially with solid state actuators).
Although numerous approaches for the optimization of actuator systems have been documented in the literature, they are not very suitable for the above mentioned objective of an integrated optimization of actuator and compliant mechanism. With the help of the present project, a contribution to the solution of the problem is to be made in the form of an optimization-based design method for active compliant systems.
A Posterior Adaptation of the Stiffness of Compliant Mechanisms
| Funding agency: | DFG |
| Research association: | |
| Duration: | 24 Months |
| Start time: | May 2019 |
| Editor: | Kristian Mauser |
| Further Information: | DFG-Project |

Compliant mechanisms use the deformability of their material to achieve a predefined motion rather than using sliding and rolling components as it is the case with conventional mechanisms. The functional principle requires that strain energy is stored when a compliant mechanism is deflected. With a defined amplitude of movement, the value of the strain energy is determined by the structural stiffness of the mechanism. From the application point of view, the latter is in a field of tension: On the one hand, there are applications in which the stiffness is desired, e.g. with tweezers to generate a restoring force; On the other hand, the stiffness reduces the efficiency of the mechanism during an energy transfer from the mechanism input to the output.Once a compliant mechanism is designed and manufactured, it usually has a defined stiffness. If the mechanism is to be used in different applications with different stiffness requirements, the result is a suboptimal system behavior. There are also applications in which the stiffness is completely undesirable, but this cannot be avoided due to the aforementioned functional principle of compliant mechanisms. It would therefore be advantageous to be able to adjust the stiffness of an existing compliant mechanism a posteriori. The approaches described in the literature in the field of compliant mechanisms partially rely on the targeted introduction of prestresses through force loading of the mechanism. However, the determination of the load is usually based on experience and intuition. With this project we aim to develop an optimization-based method to determine preload forces for the defined adaptation of the stiffness of existing compliant mechanisms.
Continuum-based design of selectively compliant mechanisms with smooth kinematics
| Funding agency: | DFG |
| Research association: | |
| Duration: | 24 Months |
| Start time: | Apr 2019 |
| Editor: | Stephanie Kirmse |
| Further Information: | DFG-Project |

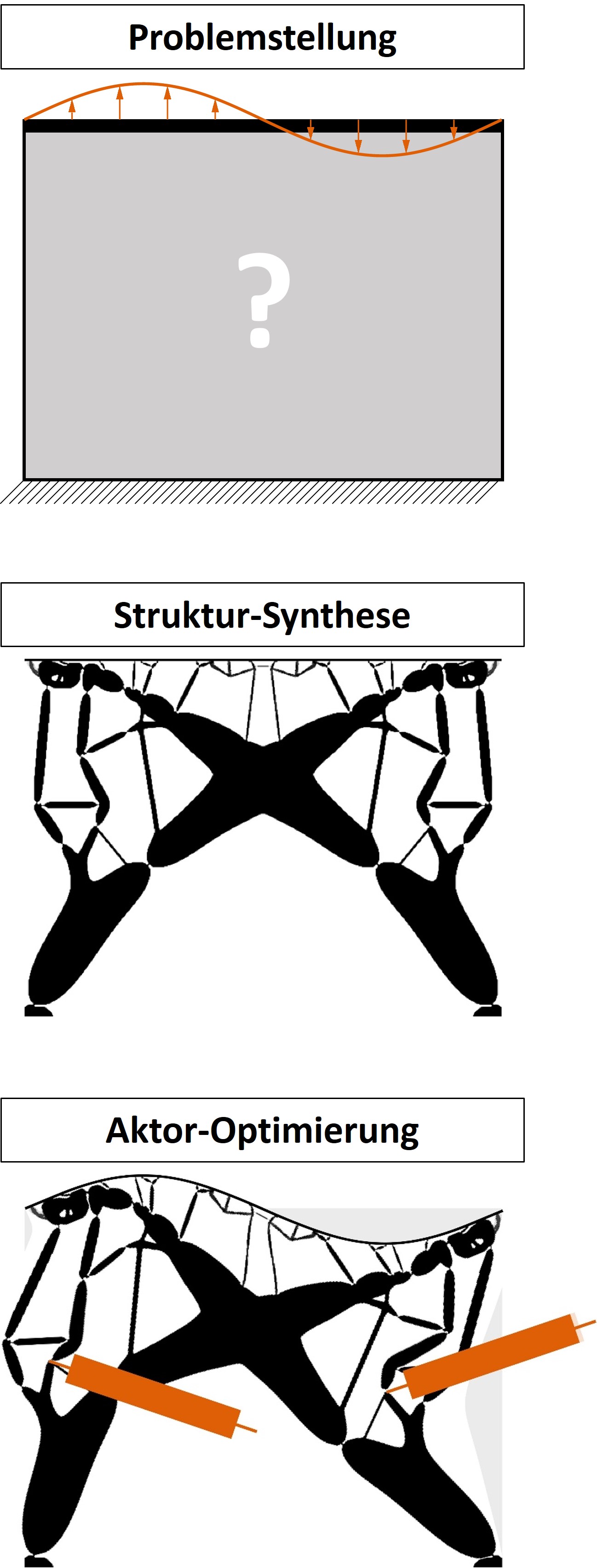
Compliant mechanisms are mechanical systems, which depict the function of a conventional mechanism, but without movable components (bearings, guide and joints). Instead, their function is based on the deformation of elastic areas. Design procedures for compliant mechanisms can be sharply divided into two categories: In the first (pseudo-static body approach), the procedure starts from a multi-body system, as with conventional mechanisms; in the other (continuum-based approach), a design space is defined in which a fixed or varying quantity of material is distributed in a defined manner. A fundamental difference between the two approaches concerns the mechanisms topology. In the first case the topology is to be assigned a-priori, while in the second case it is part of the result. This makes the design by multibody methods relatively easy, however at the price of a substantial reduction of the choice of possible layouts. Continuum-based approaches are normally based on formal optimization methods due to their inherent complexity. A further important difference is related to the kind of deformation patterns which can be achieved: multibody methods tend to generate deformation patterns with elastic strain concentrated in particular areas, while continuum based methods allow arbitrary deformation patterns including smooth shape changes. Known continuum based methods are mainly focused on the synthesis of mechanisms with a pseudo-mobility of one. The pseudo-mobility of a compliant mechanism corresponds to the number of independent kinematic quantities which are to be prescribed in order to control the static deformation of the mechanism with sufficient accuracy. General-purpose procedures able to explicitly generate mechanisms with multiple pseudo-mobility are not available. The methodology to be developed in this project is intended to remove this deficiency. In addition, the new design approach shall be able to generate mechanisms with smooth deformation patterns.The methodology to be developed in this project is of practical interest for any kinds of shape-adaptable structures, like morphing wings, adjustable seats and bed surfaces, as well as for classical transmission mechanisms for robotics and in general for automation tasks.
Vibration reduction by energy transfer using shape adaption
| Funding agency: | DFG |
| Research association: | SPP 1897 |
| Duration: | 36 Months |
| Start time: | Jan 2017 |
| Editor: | Alexander Nowak |
| Further Information: | DFG-Project |


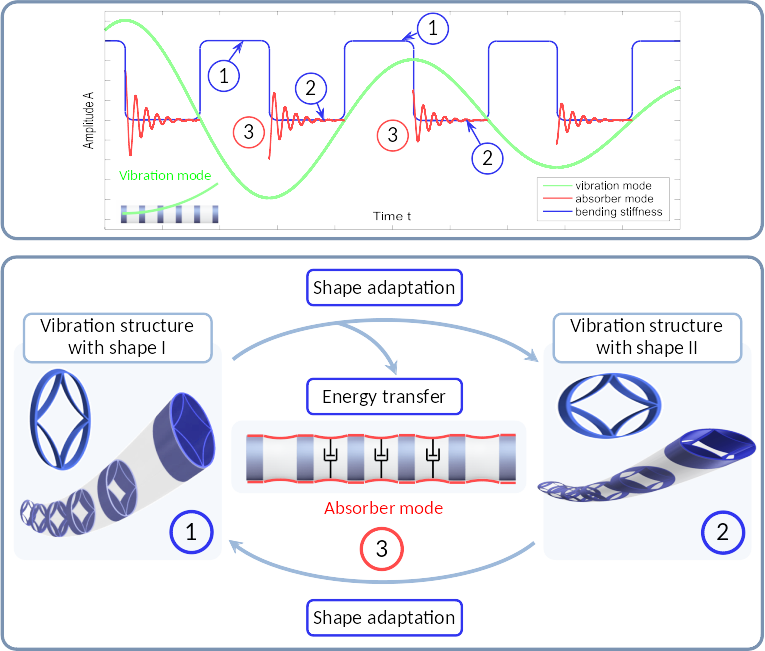
Lightweight design is one of the most important issues in engineering design. The objective is to reduce the mass of structural components for the purpose of saving costs, energy and resources in manufacturing and operation processes. However, the lighter the structure is, the more it is prone to unwanted vibrations. Such vibrations should be minimized in order to prevent the environment, products and human beings from being harmed and to maximize the lifetime of the products. Vibration reduction can be achieved by passive, semi-active or active measures, where passive means that no external energy is needed, while semi-active and active measures employ external energy to either control dissipation or directly counteract the vibrational motion, respectively. Since active measures usually do not rely on dissipation, they do not fall in the scope of the call for proposals and will not regarded in this project. In the realm of passive and semi-active measures, two general approaches can be used to reduce vibration in structures, namely that of damping, which is the dissipation of kinetic energy into another form of energy, or that of absorption, which is the transfer of kinetic energy from a critical mode into an uncritical mode. The envisioned approach will combine the concepts of damping and absorption in a novel way by integrating the functionality of a damped, tuned mass absorber into a shape adaptive structure. By dynamically adapting the stiffness of a slender, beam-like structure using shape adaption of the cross-section, kinetic energy will be transferred from the critical low-frequency bending modes into a specifically designed, higher frequency absorber mode, which can then be damped in an optimal way. Optimal design of the shape adaption mechanism and of the absorber mode will be pursued using compliant mechanisms. The dissipation will be optimized by a specifically designed friction damper.
7 Monolitix

Monolitix is a project on compliant systems that ran from 2010 to 2016 in Dübendorf near Zurich. The aim was to increase the acceptance of compliant systems and solid-state joints in industry and to implement them in commercial products. Monolitix was implemented privately, as a stock corporation under Swiss law. It was founded as a spin-off from Empa (Swiss Federal Laboratories for Materials Testing and Research) and ETH Zurich. After the infrastructural as well as personnel support by Empa ended, the company unfortunately no longer supported itself financially and had to close in 2016.
Two of the company founders and proven knowledge and experience carriers in the field of compliant systems are now part of the team of the Chair of Machine Elements and Product Development. The internet presence of Monolitix, which enjoys great popularity due to the comprehensive information on the subject, has been maintained and can be viewed here .