Monatsrätsel
Immer auf dem Laufenden über unsere neuesten Rätsel?
Einfach in die Mathriddler-Mailingliste eintragen!
Fußball - (Juli 2024)

Sind wirklich immer genau zwölf Fünfecke nötig?
Tagesplan - (Juni 2024)

Wie wahrscheinlich gibt es dann eine Reihenfolge der drei Aktivitäten, die alle drei Mehrheitswünsche berücksichtigt?
Ringe - (Mai 2024)

Ist diese Beobachtung korrekt? Wieso? Müssen dafür die Ringe gleichgroß sein?
Affine Geometrie - (April 2024)

Gibt es unter den vergangenen Monatsrätseln eines, dessen Lösung sich leicht als Inzidenzgeometrie bezeichnen lässt?
Welche Schwerpunkte hat ein Dreieck? - (März 2024)
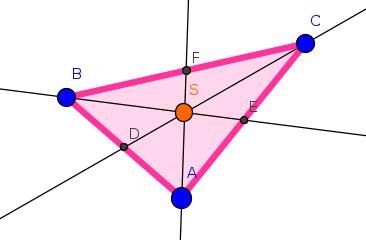
Welcher der drei Schwerpunkte ist denn nun dieser Schnittpunkt der Seitenhalbierenden und welcher nicht? Wo liegen der oder die Ausreißer (bzw. wie ist er zu konstruieren)?
Bekommt man alles umgedreht? - (Februar 2024)
Kann es sein, dass die Münzen so daliegen, dass man es nie erreicht, das alle 2024 Münzen Zahl zeigen, solange man auch nach dieser Regel Münzen umdreht? In welcher Lage gelingt es erst nach maximal vielen Münzdrehungen, alle Münzen umzudrehen?
Ergeben sich die Monate aus dem Jahr? - (Januar 2024)
Lassen sich alle Monatsnummern auf diese Art und Weise aus 2 0 2 4 erzeugen? In welchen Monaten kommt man sogar ohne Fakultätszeichen aus?
Fullerene - (Dezember 2023)

Wie viel mehr Fünfecke als Siebenecke hat ein konvexes Fulleren höchstens? Wie viel mehr sind es mindestens?
Bunte Blätter - (November 2023)

Welche Seitenverhältnisse haben das vorliegende Blatt Papier, das Goldene, das Silberne und das Bronzene Rechteck?
Soma-Würfel - (Oktober 2023)
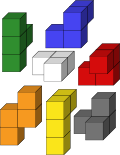
Kann man den Würfel so zusammensetzen, dass von den äußeren Teilquadraten genau drei weiß sind?
Sensen - (September 2023)
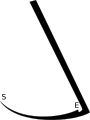
Für welchen Abstand von E zur Drehachse wird F maximal, wenn wir von fixem w ausgehen?
Urlaub - (August 2023)

Wieviele Möglichkeiten gibt es, das Wort "Urlaub" total durcheinander zu schreiben?
Reptile - (Juli 2023)

Gibt es ein Polyeder mit Loch, welches ein Reptile ist?
Hungriger Drache 5 - (Juni 2023)

Kann der Zwerg sich trotzdem an Land retten? Kann er das auch noch, wenn der Drache sogar viermal so schnell ist?
Magisches Quadrat - (Mai 2023)

Wieviele Möglichkeiten für Magische Quadrate gibt es mit vorgegebenen vier Formen und vorgegebenen vier Farben?
Dornröschen und die Münze - (April 2023)

Was soll sie antworten? Mit welcher Wahrscheinlichkeit liegt sie richtig?
Kuchen Teilen - (März 2023)

Kann ein Kreis durch 3 Sehnen in sieben flächeninhaltsgleiche Teile zerlegt werden?
Minisudoku - (Februar 2023)

Wieviele verschiedene Minisudokus gibt es?
- ()
Freudige Zeit - (Dezember 2022)

Zeige, dass es sogar fünf aufeinanderfolgende mindestens zweistellige natürliche Zahlen gibt, die Harshad-Zahlen sind!
Ohrpolygon - (November 2022)
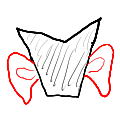
Jedes Polygon, welches mindestens vier Ecken hat, hat auch mindestens zwei Ohren.
Würfelschnitt - (Oktober 2022)
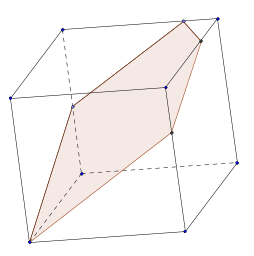
Wie muss man einen Würfel mit einem ebenen Schnitt zerteilen, damit hernach die Oberfläche möglichst groß ist?
Schatzaufteilung - (September 2022)

Welche der drei Fälle A), B) und C) sind möglich, wenn beide auch wissen, wie der jeweils andere die Dinge im Schatz bewertet -- und dies Wissen nutzen, um so viel wie möglich für sich zu bekommen?
Urlaub - (August 2022)

Wie viele verschiedene Wortkreationen lassen sich unter dieser Einschränkung aus URLAUB bilden?
Wahr oder falsch? - (Juli 2022)

Welche dieser Sätze sind wahr, welche falsch?
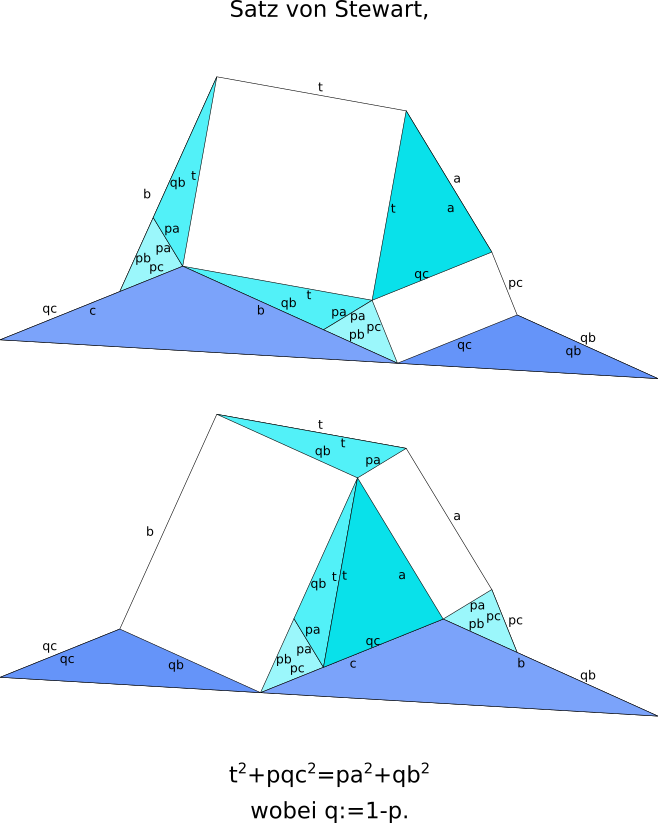
Stewarts Badewanne - (Juni 2022)
Wie sieht ein "Badewannenbeweis" des Satzes von Stewart (mit möglichst wenig "Wasser", also "möglichst trocken") aus?
Wägeproblem - (Mai 2022)

Wie viele geeichte Gewichte sind nötig, um solche Massen bis 40kg exakt auswägen zu können? Welche Massen müssen sie haben?
Halbe Sachen machen - (April 2022)
Wie viele Funktionen f gibt es, die natürliche Zahlen auf natürliche abbilden und f(f(n))=n+1 erfüllen? Wie viele Funktionen g gibt es, die natürliche Zahlen auf natürliche abbilden und g(g(n))=2n erfüllen?
Selbstberührer - (März 2022)
Findet Ihr eine Figur verschieden vom Kreis, die an Stelle von Ellipsen diese Eigenschaft hat?
Palindrom - (Februar 2022)

Der wievielte Palindromtag in der Geschichte ist der 22. Februar? Wann wird danach der nächste Palindromtag sein?
Ergeben sich die Monate aus dem Jahr? - (Januar 2022)

Lassen sich alle Monatsnummern auf die beschriebene Art aus der Ziffernfolge 2 0 2 2 erzeugen? Wo braucht man das Fakultätszeichen?
Weihnachtskugel - (Dezember 2021)

Kann sich Ulla da so sicher sein? Oder könnten die Kreise auch zu groß sein, um sechs davon auf eine solche Kugel zu malen?
Minisudoku - (November 2021)

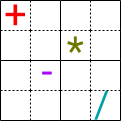
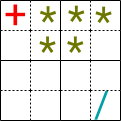
In wie viele Felder müssen mindestens Symbole eingetragen sein, damit das Minisudoku eindeutig lösbar ist?
Im Gurkenlager - (Oktober 2021)

Wie viel Prozent Masse verlieren sie, wenn ihr Wasseranteil durch Verdunstung auf 94% fällt?
Wie viele von 100000 der "Immerfrisch"-Gurken wurden aussortiert? Wie viele von 100000 der "Frischfrisch"-Gurken wurden aussortiert?
Fischhandel - (September 2021)

Wie viele Kisten sind auf einer Palette, wie viele Fische sind in einer jeden Kiste und wie viele Fische sind auf der Palette?
Schnapszahl - (August 2021)

Welche Zahlen sind dann leider keine Schnapszahlen?
Die Schnecke auf dem Gummiband - (Juli 2021)

Wird die Schnecke je das andere Ende des Gummibandes erreichen?
Bleistift - (Juni 2021)

Der verwendete Spitzer würde einen runden Bleistift so zuschneiden, dass der beschnittene Teil ein perfekter gerader Kreiskegel ist, bei dem der Durchmesser der Grundfläche halb so groß ist, wie seine Höhe. Maria betrachtet also Ihren Bleistift und grübelt nach einem neuen Matherätsel. Dabei bemerkt sie: Es liegt doch ein Rätsel offen vor ihr!
Welches Volumen hat Marias Bleistift?
Edle UG-Worte - (Mai 2021)

Wenn man die Zeichenkette "U" also beispielsweise viermal veredelt, ergeben sich nacheinander die Zeichenketten "G", "UG", "GGU", und "UGUGG". Bezeichnen wir mit b(k) für ein gegebenes k die Anzahl der Buchstaben, die das Wort hat, welches sich durch k-maliges Veredeln von "U" ergibt, ergibt sich also für k von Null beginnend an die Folge b(k) zu 1,1,2,3,5,... Nun stellt sich die Frage:
Gibt es eine einfache Bildungsvorschrift für die Folge?
Platzkarten - (April 2021)

Mit welcher Wahrscheinlichkeit ist der freie Platz sein eigener, wenn der Ehrengast noch 128 freie Plätze zur Wahl hat?
Wie ändert sich das Ergebnis, wenn der Ehrengast eine andere Anzahl an freien Plätzen zur Auswahl hat?
Die falsche Waage - (März 2021)

Ist das Ergebnis trotzdem aus den bisherigen Wägungen ablesbar, unabhängig davon, welche Wägungen Sören konkret ausgeführt hat?
Fünfeckfläche - (Februar 2021)

Welchen Flächeninhalt hat das entstehende Fünfeck?
Ergeben sich wieder die Monate aus dem Jahr? - (Januar 2021)

Lassen sich dieses wieder Jahr alle Monatsnummern aus der Ziffernfolge der Jahreszahl auf die beschriebene Art und Weise erzeugen? Für welche Monatsnummern ist das Fakultätzeichen notwendig?
Feuerwerk - (Dezember 2020)

Finde eine möglichst kurze Reihenfolge, um das Feuerwerk sicher zu zünden!
Guter Start - (November 2020)

Ist das ein kluger Zug, oder kann Kunz nun den Sieg erzwingen?
Logik - (Oktober 2020)

Gib alle Möglichkeiten für eine solche Verknüpfung an!
Münzspiel 2 - (September 2020)

Für welchen der beiden Zwerge gibt es eine Gewinnstrategie, für den älteren oder den jüngeren?
Kugelparkettierung - (August 2020)

Kommt man mit Fliesen einer Form aus, wenn die maximale Ausdehnung der Form 50 Zentimetern nicht überschreiten darf?
Schubfachschluss gecheckt - (Juli 2020)

Wie kann man die doppelt vorkommenden Zahl mit nur konstant (also nicht von n abhängig) vielen zusätzlichen Speicherzellen ermitteln?
Kann man eine doppelt gespeicherte Zahl stets mit nur konstant vielen zusätzlichen Speicherzellen ermitteln?
Aufwärts - (Juni 2020)

Kann die ewige Baumschnecke die Blätterkrone erreichen, obwohl ein Schneckimeter eben doch viel kürzer als ein Fantastimeter ist ?
1+1 - (Mai 2020)

Die Basis muss daher sicherlich eine echt komplexe Zahl sein, die als Divisor bei der ganzzahligen Division nur mit den Resten 0 und 1 auskommt, weil man sonst an der letzten Stelle ein Problem hat. Dazu muss sie aber kleinstmöglichen Betrag haben. So kommen nur die vier Zahlen 1+i, 1-i, -1+i und -1-i als Basis in Frage. Nimmt man eine der ersten beiden Alternativen als Basis, stellt sich heraus, dass 2 gar nicht darstellbar ist. Ist die Basis b eine der beiden letzten Alternativen (also -1-i oder -1+i) ergibt sich unter zuhilfenahme der im System ungültigen Ziffer 2 die Kürzungsregel "122=0" (wegen 0=(b+1+i)(b+1-i)=1b²+2b+2), was auf "2=-120=-100+(-20)" und "-20=1200" im entsprechenden Positionssystem auf "2=-120=-100+(-20)=-100+1200=1100" führt. Mehr Details findet man in der englischsprachigen Wikipedia unter Complex-base system <\br> Das Bild zeigt übrigens eine Drachenkurve: den "Twin Dragon". So sieht aus der Ferne betrachtet etwa die Menge aller ganzen Gausschen Zahlen aus, die mit höchstens 20 Stellen auskommen.
Gibt es das überhaupt? Wie lautet in einem solchen Positionssystem die Darstellung von 1+1?
A4 gefaltet - (April 2020)

Warum trifft das nicht nur ungefähr zu? Wieso folgt daraus, dass das von den umgefalteten Dreiecken nicht bedeckte Rechteck ähnlich zur Form des Originalblatts ist? Die Irrationalität welcher Zahl folgt daraus?
Geburtstagskuchen - (März 2020)

Trifft das zu? Welche Zahlen a gibt es, für die es (bis auf Kongruenz) genau ein axialsymmetrisches Sechseck aber kein Quadrat mit ganzzahligen Seitenlängen gibt, dessen Flächeninhalt gleich 4a ist?
Wie rund kann das sein? - (Februar 2020)
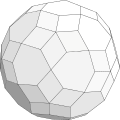
Kann es eine Kugel geben, die alle Kanten berührt?
Ergeben sich die Monate aus dem Jahr? - (Januar 2020)
Lassen sich dieses Jahr alle Monatsnummern aus der Ziffernfolge der Jahreszahl auf die beschriebene Art und Weise erzeugen?
Eigenartige Zeichen? - (Dezember 2019)

Elisas sechstes Zeichen könnte also eine 6 und ihr Spiegelbild an ihrer rechten Tangente sein.
Leider kann man aber den ersten k Gliedern einer Folge ohne zusätzliche Informationen niemals ansehen, wie das k+1-te Glied der Folge beschaffen ist. In unserem Fall hat Elisa als sechstes Glied leider ein Smiley gemalt, welches mit dem linken Auge zwinkert ;-)
Wäre die Aufgabe ein Intelligenztest, dann wäre die richtige Antwort sicherlich die mit der Sechs plus Spiegelbild. Intelligenztests prüfen (im mathematischen Teil) hauptsächlich die Fähigkeit, einfache Strukturen zu erkennen (wobei die Einfachheit ohne kulturellen Hintergrund schwer zu definieren sein dürfte). Sicher ist das eine wichtige Fähigkeit für Mathematiker.
Als Mathematikaufgabe ist diese Aufgabe aber völlig unterbestimmt, denn bei Folgen ist nicht klar, dass es überhaupt ein einfaches Bildungsgesetz geben muss. Es fehlen hier Informationen, die die Menge der in Betracht zu ziehenden Bildungsgesetze so weit einschränken, dass das nächste Zeichen sich eindeutig ergibt. In diesem Sinne ist jedes Zeichen, was einem in den Sinn kommt, gleichermaßen möglich, und auch dies gehört zum Grundwissen eines Mathematikers.
Ob Sie nun selbst gleich darauf gekommen sind, dass das nächste Zeichen völlig beliebig sein kann oder die Aufgabe als Intelligenztest gelöst haben - in jedem Fall haben Sie wertvolles mathematisches Wissen oder Können offenbart!
Beim vierten Zeichen malt sie schon wieder ein M, streicht es aber dann durch (siehe Bild links oben). Als fünftes Zeichen malt sie den Umriss eines Apfels, der unter einem Ast hängt.
Wie wird wohl das nächste Zeichen aussehen?
Münzwurf - (November 2019)

Kann es passieren, dass eine Münze dabei durchfällt?
Ist die Wahrscheinlichkeit, dass in Steffens Serie der erste Wurf "Kopf" liefert, genau 1/2? Sind die Wurfergebnisse des ersten und zweiten Wurfes bei Steffen stochastisch unabhängig?
Hungriger Drache 4 - (Oktober 2019)

Sie schwenkte ihr Zauberstäblein, verschwand in einer zartrosa Glitzerwolke und es wurde wie besprochen. Seitdem hat der Drache drei Köpfe. Die gute Fee wusste, dass in jedem Zwerg ein Mathematiker steckt. Aber das ist nur ein Grund, warum sie dem Drachen drei Wünsche erfüllte. Die Rettung aussterbender Arten lag allerdings nicht im Vordergrund.
Warum war die Fee in diesem Fall gut? Kann ein gefangener Zwerg nun etwa doch sicher den Ausgang erfragen?
Goldener Herbst - (September 2019)

Gibt es ein rechtwinkliges Polygon (aufeinanderfolgende Seiten stehen senkrecht, es sind aber auch Innenecken erlaubt), das man in zwei zu ihm ähnliche Polygone zerschneiden kann, deren Flächenverhältnis der goldene Schnitt ist?
Schatten - (August 2019)

Wie muss der Würfel ausgerichtet sein, damit er auf einer Terrasse den größten Schatten spendet?
ZündschnUhr - (Juli 2019)

Wie kann sie mit Hilfe dieser Zündschnüre eine Zeitspanne von einer Dreiviertelstunde abmessen?
Sicherer Stand - (Juni 2019)

Wo befindet sich da der Schwerpunkt der Flasche inklusive Wasser?
Würfelschnitt - (Mai 2019)

Welche regelmäßigen Vielecke kann man sonst noch als ebene Schnittflächen beim Zerschneiden eines Würfels erhalten?
Ein Osterei - (April 2019)
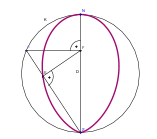
Wirklich auf der SPITZE? Bestimme den Krümmungsradius der Eikurve in S! Gibt es in S überhaupt eine eindeutig bestimmte Tangente?
Wettrennen - (März 2019)

Das Quadrat der Flugzeit des Käfers (in 10s als Einheit) ergibt sich nach Pythagoras zu (1+4+9)/36=14/36=7/18. Die Spinne kann die gegenüberliegende Ecke über eine geeignete lange Kante (im Verhältnis der Längen der von Start bzw. Zielecke zu dieser verlaufenden kurzen Kanten erreichen - Klappt man die beiden Seiten der Box, auf denen sie unterwegs ist auf, wird ihre Bahn zur Diagonale eines Quadrats von 3dm Kantenlänge. Das Quadrat ihrer Krabbelzeit (mit 10s als Geschwindigkeitseinheit) ist also 18/49<18/48=3/8<7/18. Deswegen ist die Spinne eher am Ziel.
Wer hat die kürzere Strecke zu absolvieren, und warum?
Wer ist eher am Ziel?
Münzspiel - (Februar 2019)

Finde eine Strategie, mit welcher der beginnende Spieler in jedem Fall nicht verliert.
Pärchenabend - (Januar 2019)

Peter, ein anwesender Mathematiker, fragt am Ende der Feier alle Anwesenden (also auch seine Partnerin), wie viele Hände sie jeweils geschüttelt haben. Dabei erhält er von jedem eine andere Antwort.
Wie viele Hände hat Peter geschüttelt?
Flicken - (Dezember 2018)

Dass ein kreisförmiger Flicken mit diesem Radius auch für alle anderen Fleckformen (geradeso) ausreicht, folgt aus dem Satz von Helly, dass in der Ebene der Durchschnitt einer Familie konvexer Punktmengen nicht leer ist, sofern nur der Durchschnitt von je dreien nicht leer ist.
In der Anwendung besteht die Familie aus allen Kreisen mit Durchmesser d um Punkte des Flecks. Die Mittelpunkte A, B und C von je drei dieser Kreise bilden ein Dreieck. Zeichnet man einen Kreisbogen über der längsten Seite mit einem Zentriwinkel von 120 Grad, so hat dieser einen Durchmesser von höchstens d (da die Seite höchstens 1dm lang ist und er der Umkreis des gleichseitigen Dreiecks mit dieser Seite ist) und der dritte Eckpunkt liegt unterhalb dieses Kreisbogens, da sein Innenwinkel der größte, also größer als 60 Grad ist. Damit liegt der Mittelpunkt dieses Kreisbogens im Durchschnitt der drei Kreise mit Mittelpunkten A, B und C und Radius d. Der Satz von Helly liefert nun die Existenz eines Punktes, der in allen Kreisscheiben unserer Familie liegt. Dieser taugt als Mittelpunkt des Flickens.
Zur Sicherheit wählt Sören den Flickendurchmesser aber einen Zentimeter größer, um rings um das Loch noch genug Überlappung zum Festnähen zu haben.
Unglücklicherweise hat Sören -- im Flickenladen angekommen -- vergessen, wie genau das Loch aussah. Was Sören sicher weiß, ist, dass egal wie man das Lineal anlegte, das Loch nur höchstens 1dm maß.
Welchen Durchmesser muss der Flicken mindestens haben, wenn er in jedem Fall das Loch überdecken soll?
Wo wohnt Kevin? - (November 2018)

Sphären zerlegen den Raum - (Oktober 2018)

Für n=4 ist die gesuchte Zahl auch tatsächlich 16. Eine schicke Variante findet man hier , wo in einer Explosionszeichnung die fünfzehn endlichen Teile illustriert sind.
Man kann auch auf der ersten Sphäre drei sich paarweise senkrecht schneidende Großkreise fixieren und die restlichen drei Sphären so wählen, dass sie die erste Sphäre jeweils in einem anderen dieser Großkreise schneiden. Die Großkreise zerlegen die erste Sphäre in 8 Teile und jeweils auf Innen und Außenseite jedes dieser Teile grenzt ein anderer entstandener Teil des Raumes an.
Ist a(n) die gesuchte Anzahl bei n Sphären, so ist b(n)=a(n+1)-a(n) deswegen die Anzahl der Teile, in die n Kreise eine Sphäre maximal zerlegen und c(n)=b(n+1)-b(n) die Anzahl der Teile, in die n Kreisbögenränder (also 2n Punkte) einen Kreis zerlegen. Damit ist c(n) eine arithmetische Folge erster Ordnung und a(n) eine arithmetische Folge dritter Ordnung. Wegen a(1)=b(1)=c(1)=c(2)-c(1)=2 ergibt sich a(n)=2(1+(n-1)+(n-1)(n-2)/2+(n-1)(n-2)(n-3)/6). Wer diesen Schluss nicht mag, kann die Formel auch für n von 1 bis 4 prüfen, denn durch vier Werte ist eine arithmetische Folge dritter Ordnung eindeutig bestimmt.
In wie viele Teile kann man den dreidimensionalen Raum mit vier Sphären höchstens zerlegen?
In wie viele Teile kann man ihn mit n Sphären höchstens zerlegen?
Drei Fünfecke - (September 2018)
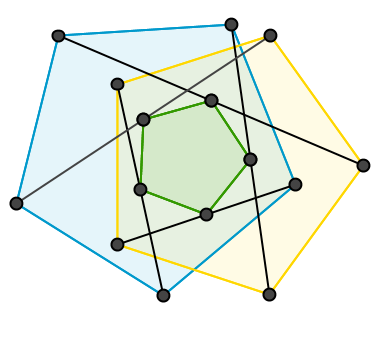
Finde einen möglichst anschaulichen Beweis, dass die Mittelpunkte der Strecken A-A', B-B', C-C', D-D' und E-E' ebenfalls ein regelmäßiges Fünfeck bilden.
Schneewittchen und die 8 Zwerge... oder doch nicht - (August 2018)

Bevor Schneewittchen geboren wurde, kam ein gemeiner Zauberer zu den 8 Zwergen und hielt sie in ihrer Hütte gefangen. Nach ein paar Tagen wurde dem Zauberer langweilig, und er entschied sich, ein Spiel mit den Zwergen zu spielen:
Ihr stellt euch hintereinander auf. Anschließend setze ich euch nacheinander verdeckt entweder einen roten oder einen blauen Hut auf den Kopf. Damit könnt ihr nur die Hüte der Zwerge sehen, die vor euch stehen. Dann frage ich euch nacheinander, beginnend mit dem letzten, welche Farbe euer Hut hat. Ratet ihr richtig, lasse ich euch frei, ratet ihr falsch, so verwandle ich euch sofort in eine Maus. Bevor wir beginnen, dürft ihr euch kurz beraten.
Finde eine Strategie, möglichst viele Zwerge zu retten.
Landesgartenschau - (Juli 2018)

Gäbe es zwei Stellen, wo der Turm stehen könnte, so würde die kubische Funktion auf die Gerade durch die beiden Stellen eingeschränkt zwei Maxima haben, wäre also nicht kubisch. Das kubische Polynom bleibt bei affinen Transformationen des zu grunde gelegten Koordinatensystems kubisch, also auch bei derjenigen, die A, B und C zyklisch permutiert. Bei dieser muss dann aber das Polynom sogar in sich selbst übergehen, weswegen auch die mögliche Position des Turmes in sich selbst übergeht. Daher kann der Turm auf der Karte nur im Schwerpunkt des Dreiecks aus den Punkten A, B und C liegen.
Welche Möglichkeiten gibt es für die Position des Aussichtsturms auf der Karte?
Eisverkauf - (Juni 2018)

Nehmen wir an, es geht nicht gut, d.h. er muss nochmal los, Wechselgeld beschaffen. In dem Moment stehen in der Restschlange 21 Leute mehr mit einzelnen Euros als solche ohne. Diese Ereignisse sind die ungünstigen. Was nun passiert, ändert daran nichts mehr. Also dürfen wir uns vorstellen, alle Leute in der Restschlange nutzen nun die Gelegenheit und gehen erstmal anderen Geschäften nach, stellen sich dann aber wieder in der gleichen Reihenfolge an -- wobei allerdings die Leute die vorher passend zahlen konnten, nun nur noch eine zwei Euro Münze haben, die andern dafür aber passend zahlen können.
In jedem solchen Fall sinkt die Zahl der Leute, die passend Zahlen können, um genau 21. Der Eisverkäufer, der von den Zwischengeschäften nichts weiß, erlebt dann also nur 29 Leute, die passend zahlen können, aber 71 Leute, bei denen das nicht der Fall ist. In dieser Situation hätte das Wechselgeld nie gereicht. Wäre das aber die Ausgangssituation gewesen, hätte es nur 29 über 100 Ereignisse gegeben, allerdings hätte er bei gleichem Verhalten der Restschlange gerade die ursprüngliche Ausgangssituation wieder vorgefunden. Es gibt also eine Bijektion zwischen all diesen 29 über 100 Ereignissen und den ungünstigen Elementarereignissen, weswegen die gesuchte Wahrscheinlichkeit 1-(100!/(29!71!))/(100!/(50!50!))=1-(50*49*...*30)/(51*52*...*71), also ungefähr 0.9995 bzw. 99.95% beträgt.
Von den hundert Kunden des Tages wird wohl genau die Hälfte den Euro passend haben, die andere Hälfte hat aber wenigstens eine 2-Euro Münze und jeder wird wohl genau ein Eis kaufen.
Er geht davon aus, dass jede Reihenfolge der Kunden gleichwahrscheinlich ist.
Mit welcher Wahrscheinlichkeit reicht unter diesen Voraussetzungen das Wechselgeld?
Einsturzgefahr - (Mai 2018)

Zwerg 1 - 10 Minuten
Zwerg 2 - 5 Minuten
Zwerg 3 - 2 Minuten
Zwerg 4 - 1 Minute
Wie schnell können die Zwerge entkommen?
Verzweifelter Kellner - (April 2018)

Kann Peter es schaffen, 6 Weizenbiergläser auf dem Tablett unterzubringen, auf dem für 7 nicht genug Platz war?
Schokolade teilen - (März 2018)

Wenke kann den Sieg erzwingen, wenn die senkrechte Halbierungszahl größer ist als die waagerechte -- und zwar indem sie immer ein solches Schokoladenrechteck in zwei etwa gleichgroße Teile teilt, in welchem diese Bedingung zutrifft.
Dann findet Stefan nämlich nur solche Rechtecke vor, in denen die waagerechte Halbierungszahl höchstens so groß ist wie die senkrechte. Er muss daher wenigstens ein Schokoladenrechteck für Wenkes nächsten Zug produzieren, oder er kann nicht mehr teilen.
Ist umgekehrt die senkrechte Halbierungszahl höchstens so groß wie die waagerechte, so kann Stefan den Sieg analog erzwingen, nun produziert Wencke in jedem Zug ein Rechteck, dessen waagerechte Halbierungszahl größer ist wie die senkrechte -- und dieses kann Stefan dann jeweils in zwei etwa gleichgroße Stücke teilen.
Bei welchen Größen der Schokolade (Anzahl Plätzchen waagerecht x Anzahl Plätzchen senkrecht) kann Wenke den Sieg erzwingen?
Ein Himmel voller Sterne - (Februar 2018)

Im übrigen ist dies eine Illustration des Olberesschen Paradoxons, dass unser Sternenhimmel finster ist, obwohl wir doch überall Sterne (bei unendlichem homogenen Universum) oder den Urknall (aktuelles Modell) sehen würden. Aufgelöst wird dies im aktuellen Modell durch Expansionsrotverschiebung -- leider scheint sich die Expansion aber entsprechend dieses Modells zu beschleunigen, was einer Verletzung des Energieerhaltungssatzes in kosmischen Größenordnungen gleichkommt. Die bisherigen Reparaturversuche dieser Unschönheit münden in dunkler Energie...
An allen anderen Punkten (außer dem Ursprung) befinden sich die Mittelpunkte von vergleichsweise winzigen gleichhellen kugelförmige Sternen, die alle den gleichen Radius haben.
Zeige, dass trotz der Winzigkeit der Sterne im Vergleich zu ihren gigantischen Abständen jeder (geometrische) Strahl vom einsamen Betrachter aus einen Stern trifft; der ganze Himmel also so hell leuchten müsste wie die Sternenoberfläche, wenn das Licht nicht anderweitig aufgehalten oder abgelenkt würde.
Hungriger Drache #3 - (Januar 2018)

Zur besseren Darstellung schreiben wir die Farben, die die Zwerge auf der Stirn haben, in ein Tupel, zum Beispiel (rs,rs,rr). Das würde bedeuten, dass Zwerg 1 und Zwerg 2 jeweils einen roten und einen schwarzen Punkt auf den Stirnen haben, und der dritte Zwerg zwei rote Punkte auf der Stirn hat.
Um zu einer Lösung des Rätsels zu gelangen, gehen wir der Reihe nach vor:
Erste Fragerunde:
Zwerg 1 würde "Ja" sagen, sobald er bei den anderen Zwergen zweimal dieselbe Farbe entdeckt, damit können wir also (rr,ss,ss) und (ss,rr,rr) ausschließen. Analog gehen wir bei dem zweiten Zwerg vor, dieser würde aus demselben Grund "Ja" sagen, also schließen wir auch (ss,rr,ss) sowie (rr,ss,rr). Gleiches gilt auch für den dritten Zwerg, somit schließen wir (rr,rr,ss) sowie (ss,ss,rr) aus. Außerdem überlegen wir uns folgendes. Würde der dritte Zwerg sehen, dass auf den Stirnen der anderen Zwerge jeweils einmal "rr" und einmal "ss" aufgemalt sind, so wüsste er, dass er nur "rs" haben kann, andernfalls hätte entweder Zwerg 1 oder Zwerg 2 bereits mit "Ja" geantwortet. Somit schließen wir auch (rr,ss,rs) und (ss,rr,rs) aus.
Zweite Fragerunde:
Ähnlich sieht die Überlegung von Zwerg 1 aus. Er würde "Ja" sagen, falls er "rr" und "ss" sehen würde, denn dann wüsste er, dass er "rs" hat. Er würde aber auch "Ja" sagen, falls er auf den anderen Stirnen "rr" und "rs" bzw. "ss" und "rs" sehen sollte, denn in diesem Fall wüsste er ebenfalls, dass er nur "rs" haben kann. Folglich können wir (rs,rr,ss) und (rs,ss,rr) sowie (rs,rr,rs) und (rs,ss,rs) ausschließen.
Wenn der zweite Zwerg jetzt aufgepasst hat, weiß er, dass er nur noch "rs" haben kann. Tipp: Einfach mal einen kleinen Baum mit allen Möglichkeiten aufmalen und die ausgeschlossenen Möglichkeiten wegstreichen.
Liebe Gäste, bevor ich euch verspeise, möchte ich euch noch eine Möglichkeit geben, zu entkommen. Als erstes male ich jedem von euch Zwergen zwei Punkte auf die Stirn, die jeweils rot oder schwarz sein können. Dabei verwende ich jeden Stift maximal 4 mal. Ihr könnt also die Punkte auf den Stirnen der anderen Zwerge erkennen, nicht aber eure eigenen.
Anschließend frage ich euch der Reihe nach, ob ihr die Farbe der Punkte auf eurer Stirn wisst. Dabei dürft ihr nur mit "Ja" oder "Nein" antworten. Sobald der erste von euch mit "Ja" geantwortet hat, muss er die Farbe(n) auf seiner Stirn nennen, sonst verspeise ich euch direkt. Antwortet der Zwerg richtig, lasse ich euch frei. Wichtig: Ihr dürft euch vorher nicht absprechen.
Das Spiel nimmt seinen Lauf:
Zwerg 1: "Nein"
Zwerg 2: "Nein"
Zwerg 3: "Nein"
Zwerg 1: "Nein"
Zwerg 2: "Ja"
Welche Farben hat Zwerg 2 auf der Stirn?
Lam Soyd und seine Päckchen - (Dezember 2017)
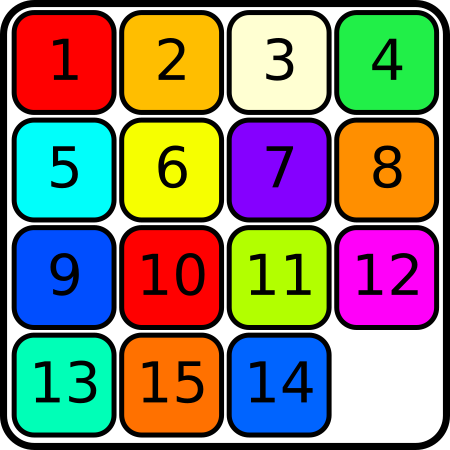
Verschiebt man den leeren Platz horizontal, dann ändert sich die Fehlstandszahl um 1, da die 16 mit einer anderen Zahl den Platz tauscht. Verschiebt man den leeren Platz vertikal, dann kann man sich überlegen, dass sich die Fehlstandszahl um eine ungrade Zahl ändert. Wenn nach einer gewissen Anzahl an Zügen das leere Feld wieder unten rechts liegt, dann hat man eine gerade Anzahl an Zügen durchgeführt. Dabei hat sich die Fehlstandszahl um eine gerade Zahl geändert. Da sie am Anfang 1 war, kann sie am Ende also nicht 0 sein und somit ist mindestens ein Paar an Päckchen noch vertauscht.
Der Weihnachtsmann kann den Wichteln also sagen, dass Lam Soyds Problem unlösbar ist.
Der Name "Lam Soyd" ist eine Hommage an den berühmten Rätselspezialisten Sam Loyd. Dieser hat einen Preis von 1000 USD auf die Lösung dieses Rätsels ausgeschrieben. Es kann davon ausgegangen werden, dass er bereits wusste, dass das Rätsel unlösbar ist.
In der Variante, die der oberschlaue Zwerge anspricht, kann das Rätsel gelöst werden. Dann muss nämlich das leere Feld in die obere linke Ecke gebracht werden. Der Nachweis, das dies möglich ist, ist allerdings etwas aufwendiger. Eine Möglichkeit besteht darin, sich zu überlegen, dass ein \(2\times3\)-Feld in eine beliebige Anordnung (mit derselben Parität) gebracht werden kann. Dann kann man sich durch das gesamte Feld "hangeln".
Mehr Informationen zu dem Rätsel finden sich auch in der Wikipedia.
Da es viele clevere Weihnachtswichtel gibt, verspricht Lam Soyd eine Belohnung von 1.000 Schokotalern, für den Wichtel, der seine Päckchen wieder in Ordnung bringt.
Nun hat der Weihnachtsmann ein Problem: Alle Wichtel versuchen nun, Lam Soyds Problem zu lösen und vernachlässigen dabei ihre eigentlich so wichtigen Aufgaben. Muss Weihnachten nun ausfallen?
Kannst du dem Weihnachtsmann helfen, dass die Wichtel ihre Arbeit wieder aufnehmen?
Verteilung von Credit Points - (November 2017)

Der ranghöchste Student macht den Verteilungsvorschlag (98,0,1,0,1), wobei er sich die 98 Credit Points gibt. Die anderen Studenten überlegen kurz und der Vorschlag wird nach Abstimmung angenommen ohne das jemand exmatrikuliert wird, aber warum?
- Fall 1: Bis auf Student D und E sind alle exmatrikuliert. Jetzt kann D den Verteilungsvorschlag (100,0) machen und gewinnt bei der Abstimmung, da bei Unentschieden seine Stimme mehr Gewicht hat.
- Fall 2: Bis auf die Studenten C, D und E sind alle exmatrikuliert. C braucht genau eine weitere Stimme, um eine vorgeschlagene Verteilung durchzubekommen. C und E wissen, dass E leer ausgeht, falls nur noch D und E übrig bleiben, also reicht der Verteilungsvorschlag (99,0,1) aus, damit E zustimmt.
- Fall 3: Die Studenten B, C, D und E sind übrig. B braucht eine weitere Stimme, um seinen Vorschlag durchzubringen. Alle wissen, dass D leer ausgeht, falls nur noch C, D und E übrig bleiben, also schlägt B die Verteilung (99,0,1,0) vor.
- Fall 4: Der Vorschlag (98,0,1,0,1) von Student A wird angenommen, weil C und E zustimmen.
Im Falle von n Studenten kann man bis n=202 argumentieren wie bisher.
Richtig interessant wird die Frage wieder für n>202, die Antwort findet man hier:
A Puzzle for Pirates (Students)
Der ranghöchste Student macht einen Vorschlag zur Aufteilung, dann stimmen alle ab, ob der Vorschlag akzeptiert wird. Wird der Vorschlag angenommen, erfolgt die Verteilung der Punkte dementsprechend, andernfalls wird der ranghöchste Student exmatrikuliert. Kommt es zu einer Exmatrikulation muss der ranghöchste verbleibende Student einen Verteilungsvorschlag machen und die verbleibenden Studenten dürfen abstimmen. Und so weiter... (Bei Unentschieden entscheidet die Stimme des ranghöchsten Studenten.)
- Jeder Student will immatrikuliert bleiben.
- Jeder Student möchte die Anzahl seiner Credit Points maximieren.
- Falls sich für einen Studenten keines der vorigen Kriterien ändert, entscheidet er sich immer dafür die Konkurrenz zu exmatrikulieren, also den Vorschlag abzulehnen.
Welche Verteilung der Credit Points wird sich für die 5 Studenten ergeben? Welche Studenten werden exmatrikuliert? Zusatzfrage: Was ergibt sich für n Studenten?
Der madige Apfel - (Oktober 2017)

Hat der Gang den Durchmesser d und die Länge l, so kann man im Gang jeden Punkt P mit Gesamtabstand d+l zu E und A erreichen, indem man von E aus auf der Mittellinie des Ganges bis zum P nächstgelegenen Punkt geht und dann direkt zu P und wieder zurück, um dann der Mittellinie zu A zu folgen. Damit lässt sich die Projektion des Ganges in eine Ellipse mit Brennpunkten E und A und Gesamtabstand zu den Brennpunkten höchstens d+l einsperren und der Halbierungstrick klappt, wenn d+l
Kann man den Apfel so durch einen ebenen Schnitt in zwei Hälften teilen, dass eine der Hälften vom Madengang sicher höchstens berührt wird?
Wer gewinnt? - (September 2017)
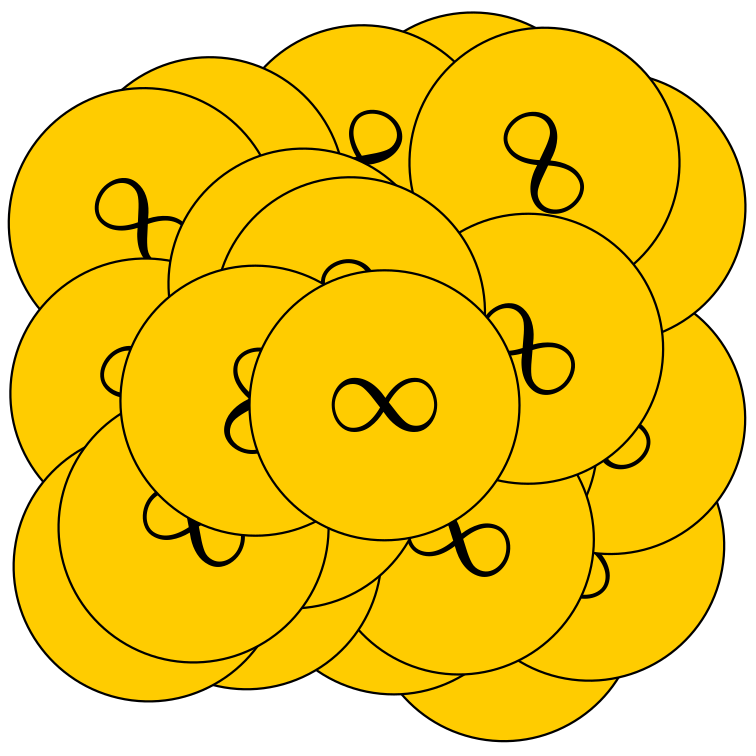
Angenommen, es wird nur mit einer Münze gespielt. Dann nimmt der Startspieler diese Münze und hat gewonnen. Ganz ähnlich sieht es aus, wenn mit höchstens \(10\) Münzen begonnen wird. Auch dann kann der Startspieler alle Münzen wegnehmen und hat gewonnen. Wir halten also fest: Sind \(1\) bis \(10\) Münzen übrig, dann gewinnt der Spieler, der gerade am Zug ist.
Wie sieht es nun bei \(11\) Münzen aus? Der ziehende Spieler nimmt eine Anzahl zwischen \(1\) und \(10\) weg. Danach liegen zwischen \(10\) und \(1\) Münze da und der andere Spieler ist am Zug. Nach unserer vorherigen Überlegung gewinnt dieser aber und dies kann der anziehende Spieler nicht verhindern! Also: bei \(11\) Münzen wird der Spieler am Zug verlieren.
Diese Überlegung kann man nun weiterführen. Liegen zwischen \(12\) und \(21\) Münzen, dann nimmt man so viele weg, dass genau \(11\) Münzen übrigbleiben. Dann ist der andere Spieler am Zug und er wird, wie wir oben gesehen haben, verlieren.
Allgemein gilt: Liegt ein Vielfaches von \(11\) aus, dann wird man verlieren. Andernfalls ist man in einer Gewinnsituation. Um zu gewinnen, muss man immer so viele Münzen nehmen, dass ein Vielfaches von \(11\) übrig bleibt.
Wer gewinnt?
Wie sieht es aus, wenn die Spieler \(k\) Münzen haben und in jedem Zug zwischen \(n\) und \(m\) viele Münzen nehmen?
Ein neues Sofa für Familie Maulwurf - (August 2017)

Das Problem wurde von Leo Moser im Jahr 1966 gestellt. Eine deutliche Verbesserung gegenüber dem Quadrat bietet zum Beispiel ein Halbkreis mit Radius \(1\), dies führt auf eine Fläche von \(\pi/2 \approx 1.57078\). Dieser kann einfach um die Ecke rotiert werden. Es kann auch relativ einfach argumentiert werden, dass die maximale Fläche kleiner als \(2 \, \sqrt 2 \approx 2.8284\) sein muss. Der längste Stab, der um die Ecke passt hat nämlich gerade die Länge \(2 \, \sqrt 2\) (betrachte dazu den Stab, wenn er gerade um \(45^\circ\) gedreht ist). Das Sofa muss also
kürzerals \(2 \, \sqrt 2\) sein. Weiterhin kann das Sofa nicht
breiterals \(1\) sein, denn dann passt es ja gar nicht erst in den Gang. Somit kann der Flächeninhalt \(2 \, \sqrt 2\) nicht überschreiten.
Die bisher beste bekannte Lösung von Joseph Gerver hat einen Flächeninhalt von ungefähr \(2.2195\). Weiter ist bisher lediglich bekannt, dass das Sofa nicht größer als \(2.37\) sein kann. Dies wurde erst im Juni 2017 gezeigt, aber dafür musste ein Computer 20 Tage lang rechnen.
Schließlich können wir nur hoffen, dass die Familie Maulwurf sich mit einem Gerver-Sofa zufrieden stellt.
Wie groß kann das Sofa für Familie Maulwurf werden? Kannst du zeigen, dass es kleiner als ein bestimmter Wert sein muss?
4 Zwerge und der Wackeltisch - (Juli 2017)

Ein schönes Video zu dem Problem findet sich auf Youtube.
Kannst du den vier Zwergen bei der Lösung ihres Problems helfen?
Die Maus und ihr Käse - (Juni 2017)

Hier schafft es die Maus, denn ein gültiger Pfad besteht darin, in einer Ecke, zum Beispiel der linken unteren, zu beginnen, dann einmal außen entlang zu gehen und zum Schluss das mittlere Stück zu verspeisen.
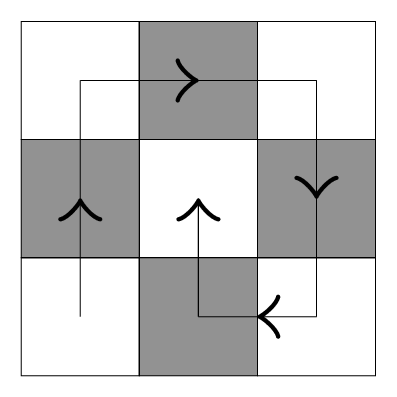
Man stelle sich das \(3\times3\) Quadrat wie ein Schachbrett eingefärbt vor. Nehmen wir an, dass das linke untere Feld, in dem die Maus beginnt, weiß ist. Dann sind die beiden angrenzenden Felder schwarz, und so weiter. Insbesondere ist das mittlere Feld, welches sich die Maus bis zum Schluss aufheben will, auch weiß. Die Regel, dass die Maus sich immer ein benachbartes Feld durchfrisst, übersetzt sich dazu, dass sie immer abwechselnd weiße und schwarze Felder besucht. Insgesamt gibt es neun Felder, wovon 5 weiß und 4 schwarz sind. Da sie in einem weißen startet, muss ihr Pfad auch in einem weißen enden, und weil das mittlere weiß ist, schafft sie es auch, das mittlere zum Schluss zu fressen.
Nun zum eigentlichen Problem:
Auch für 3 Dimensionen stellen wir uns wieder eine Färbung in abwechselnd schwarze und weiße Würfel vor, die Ecken sind wieder weiß. Jetzt kommt es jedoch dazu, dass der mittlere Würfel schwarz ist, womit wir schon gezeigt haben, dass es keinen Pfad geben kann, bei dem das mittlere Stück als letztes besucht wird. Es gibt nämlich 27 Würfel, wovon 14 weiß und 13 schwarz sind. Da die Tour in einem weißen Würfel beginnt, muss sie also auch in einem weißen Enden. Da wir aber schon festgestellt haben, dass das mittlere Feld schwarz ist, gibt es für die Maus keinen Weg, den mittleren Würfel zum Schluss zu fressen.
Und zum Schluss das Problem in \(n\) Dimensionen:
Ab jetzt ist im Grunde klar, wie es weitergeht. Durch abwechselnde Färbung der Würfel stellen wir fest, dass für gerade Dimensionen \(n\) (also \(n = 2,4,6,\ldots\)) das mittlere Feld weiß ist, und wir somit auch immer einen Pfad finden, wohingegen das mittlere Feld bei ungeraden Dimensionen \(n\) (also \(n = 1,3,5,\ldots\)) schwarz ist und kein gültiger Pfad existiert.
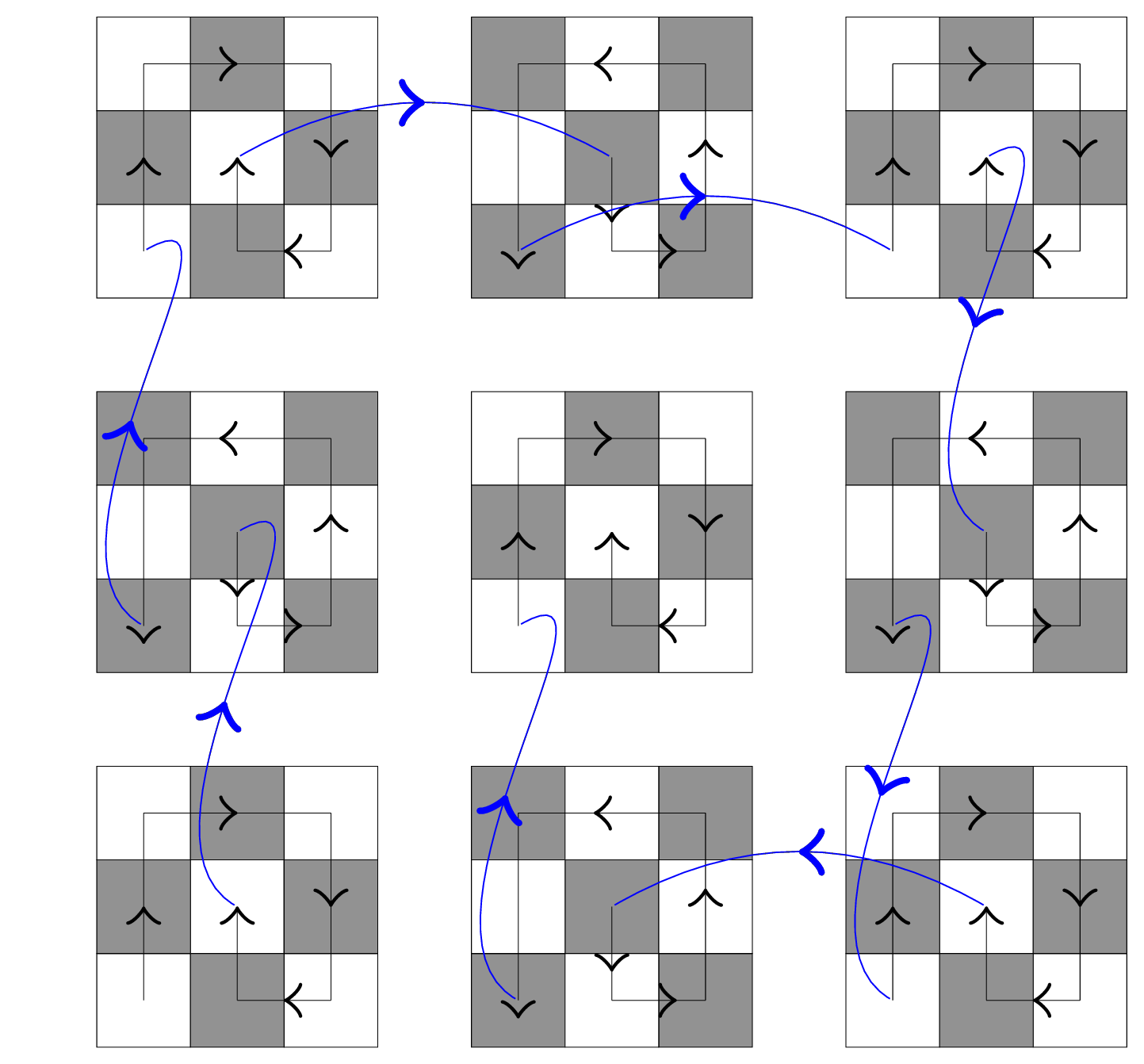
Kannst du der Mathe-Maus Margit helfen einen Pfad zu finden, bei dem sie sich das mittlere Stück bis zum Schluss aufheben kann?
Hilfe: Wenn dir die Vorstellung in 3 Dimensionen schwer fällt, frage dich, wie das Problem mit einer 2-dimensionalen Maus und einer \(3 \times 3\) Käseplatte aussieht?
Zusatzfrage: Wie sieht das Problem mit einer \(n\)-dimensionalen Maus und einem \(n\)-dimensionalen Käsewürfel mit den Abmessungen \(3 \times 3 \times \ldots \times 3\) aus?
Münzwägeanstalt - (Mai 2017)

ggg, grg, rlg, lgg, grl, rll, lgl, grr, rlr, lgr, ggr, rrl und llg, gibt alle außer ggg in der Wägeanstalt ab und in seinem Wägeplan ist in der ersten Wägung jede Münze mit erstem Zeichen l auf die linke Waagschale zu legen, jede Münze mit erstem Zeichen r auf die rechte Waagschale und
die mit g als erstem Zeichen werden weggelassen, in Wägung 2 und 3 wird analog entsprechend dem 2. bzw. 3. Zeichen verfahren.
Der Ausgang der drei Wägungen lässt sich ebenfalls mit einer Folge W von drei Zeichen beschreiben, wobei das erste den Ausgang der ersten Wägung (l: links schwerer, r: rechts schwerer, g: beide Seiten gleichschwer), das zweite und dritte den Ausgang der zweiten bzw. dritten Wägung entsprechend kodieren.
Die besondere Münze ist nun jene, die entweder W als Namen trägt, oder deren Name sich durch Vertauschung der Zeichen r und l in W ergibt. War die Münze nicht ggg so ist sie im ersteren Fall schwerer und im letzteren Fall leichter als die anderen, ansonsten bleibt diese Frage offen.
Allgemein lässt sich jeder Wägeplan mit \(w\) Wägungen durch eine derartige Benennung der Münzen kodieren, da er ja für jede Wägung festlegen muss, welche Münze links, welche rechts und welche nirgendwo hingelegt werden soll. Er funktioniert genau dann (und zwar analog zu oben), wenn er verwechslungssicher (keine zwei Münzen werden stets auf die gleiche Schale gelegt, und keine zwei Münzen werden stets auf verschiedene Schalen gelegt, wenn also verschiedene Münzen verschiedene Namen haben, die auch nicht durch konsequente Vertauschung von
l und r auseinander hervorgehen —
ansonsten kann man, falls eine der beiden Münzen die besondere ist, das Wägeergebnis auch erhalten wenn die andere die besondere ist)
und ausgewogen (in jeder Wägung gibt es gleichviele Münzen links und rechts) ist.
Nun kann man aber nur \((3^w+1)/2\) verschiedene Namen vergeben, weil außer gg...g alle mit einem anderen verwechselt werden können.
Von so benannten Münzen würden aber \(3^{w-1}\) an der ersten Wägung teilnehmen was ungerade ist und in einem ausgewogenen Wägeplan nicht geht.
Also kann ein funktionierender Wägeplan nur für höchstens \((3^w-1)/2\) Münzen existieren.
Hat man einen solchen Wägeplan für \(w-1\) Wägungen, in dem rr...r und ll...l nicht vorkommt, erhält man einen solchen für w Wägungen in dem rrr...r und lll...l nicht vorkommt, indem man an jeden der Namen außer ggg...g einmal ein r, einmal ein l und einmal ein g anhängt,
und die vier Namen ggg...gg, ggg...gr, rrr...rl und lll...lg hinzufügt.
Der größte Wägeplan mit einer Wägung enthält nach dem Vorgesagten nur den Namen g, funktioniert also tatsächlich mit \((3^1-1)/2\) Münzen.
Mit jeder hinzukommenden Wägung wird die vorhergehende Anzahl verdreifacht und es kommt noch \(1\) hinzu. Da diese Rekursion aber auf unsere obere Schranke in Abhängigkeit von \(w\) zutrifft, erhalten wir mit der beschriebenen Konstruktion tatsächlich einen funktionierenden
Wägeplan für \((3^w-1)/2\) Wägungen.
Für zwei Wägungen ergeben sich etwa die Namen gg, gr, rl, lg. Im nächsten Schritt ergeben sich die von Zwergli verwendeten Namen usw.
Es sei noch erwähnt, dass auch wenn Zwergli nicht genau zwei aber weniger als \((3^w-1)/2\) Münzen mit einer besonders gewichteten besitzt, ein Wägeplan existiert, welcher mit \(w\) Wägungen die besondere Münze findet.
g (gleichschwer), l (links schwerer) und r (rechts schwerer).
Da er nicht drei Anträge schreiben will, denkt er darüber nach, einen Wägeplan gleich für alle drei Wägungen zu schreiben,
kann dabei aber für die späteren Wägungen nicht auf die Ergebnisse der vorhergehenden zurückgreifen.
Ist es Euch trotzdem möglich, für Zwergli einen solchen Wägeplan für drei Wägungen zu erstellen, mit dem er die besondere Münze aus 13 Münzen sicher herausfindet?
Zusatzfrage: Aus wie vielen Münzen kann man die besondere mit einem solchen Wägeplan für \(w\) Wägungen ermitteln?
Das Schloss und die Prinzessin - (April 2017)

Dabei hilft es, sich zu überlegen, dass die Parität (siehe auch Märzrätsel) ihres Zimmers immer wechselt. Das bedeutet nichts anderes, als dass sie sich in einer Nacht in einem Zimmer mit gerader Nummer aufhält und in der nächsten Nacht in einem mit Zimmer mit ungerader Nummer.
In der 1. Nacht kann der Prinz nur raten, er sollte aber eines der mittleren Zimmer wählen, sagen wir Zimmer 2. Ist die Prinzessin dort, freut er sich, ist sie nicht dort, schaut er in der nächsten Nacht in Zimmer 3.
Ist die Prinzessin dort auch nicht, weiß der Prinz schon, dass sie in der ersten Nacht in Zimmer 1 oder 3 gewesen sein muss.
Damit war sie in der zweiten Nacht in Zimmer 2 oder 4, in der dritten Nacht wird sie somit in Zimmer 1 oder 3 sein. Falls sie von Zimmer 4 kommt, bekommen wir sie auf alle Fälle, indem wir es in Zimmer 3 versuchen. Wenn sie dort nicht ist, kann sie in der dritten Nacht nur in Zimmer 1 sein, und von dort kann sie in der nächsten Nacht nur ins Zimmer 2. Damit haben wir sie spätestens in der vierten Nacht gefunden.
Diese Strategie lässt sich ohne weiteres auf ein Schloss mit \(M\) Schlafzimmern erweitern. Hier versuchen wir die Zimmer in folgender Reihenfolge: \(2, 3, ..., M-1\).
Jetzt wissen wir, dass sie sich am Anfang nicht in einem Zimmer mit gerader Nummer aufgehalten hat, nun müssen wir ihr nur noch den Weg abschneiden, das heißt, die Zimmer in umgekehrter Reihenfolge: \(M-1, M-2, ..., 3, 2\) durchsuchen. So haben wir die Prinzessin in der "\(2\cdot(M-2) = 2M - 4\)"ten Nacht gefunden.
Jede Nacht kommt ein Prinz vorbei, der die Prinzessin gerne treffen würde. Von außen ist nicht ersichtlich, in welchem Zimmer die Prinzessin schläft. Er darf sich jedoch ein Zimmer aussuchen, in das er hineinschaut. Ist die Prinzessin dort, freut sich der Prinz. Ist sie nicht in dem Zimmer, kommt der Prinz in der darauffolgenden Nacht wieder und darf es erneut versuchen.
Könnt ihr dem Prinzen garantieren, dass er die Prinzessin in höchstens \(N\) Nächten findet?
Zusatzfrage: Wie lange würde der Prinz maximal benötigen, um eine Prinzessin in einem Schloss mit \(M\) Schlafzimmern zu finden? Denn welcher Prinz hätte nicht gerne eine Prinzessin mit \(M\) Schlafzimmern.
Letzte Chance - (März 2017)

Da die geratene Reihenfolge durch eine endliche Folge von sukzessiven Vertauschungen aktuell aufeinanderfolgender Pinguine aus der richtigen Reihenfolge entsteht, braucht man nur zu prüfen, ob das einmalige Vertauschen aufeinanderfolgender Pinguine in der geratenen Reihenfolge zu einem Fehler führen kann.
Die beiden vertauschten Pinguine ändern ihr Verhalten, weil ihre geratenen Nummern die Parität ändern, die von ihnen gesehene Permutation aber nicht.
Die anderen Pinguine ändern ihr Verhalten aber auch, weil sich für sie die geratenen Nummern nicht ändern, dafür aber die Parität der von ihnen gesehenen Permutation.
Damit bleibt es aber bei korrektem Verhalten, weil lediglich linker Flügel und rechter Flügel bei allen vertauscht werden.
Anmerkung: Das könnte offenbar auch bei erheblich größeren Durchfallraten funktionieren aber eben nur, wenn alle durchgefallenen Pinguine die Parität einer Permutation und einer Zahl richtig bestimmen und richtig negieren können und keiner eine links-rechts-Schwäche hat. Die Wahrscheinlichkeit dafür sinkt freilich exponentiell mit der Anzahl der durchgefallenen Pinguine, weswegen der freundliche Professor dann wohl eher Vierergruppen bilden würde.
Gibt es eine Strategie, sodass die Pinguine doch noch alle bestehen?
Walzerwunder? - (Februar 2017)

Ist das wirklich so überraschend oder geht das unabhängig von der Wahl des Standortes am Start und der Form des aufgezeichneten Vielecks?
Hungriger Drache #2 - (Januar 2017)

Der nächste Zwerg sieht nun die anderen acht Hüte und kann deren Summe bilden. Dann kann er mit der Information des obersten Zwerges auf seine eigene Hutfarbe schließen. Alle anderen Zwerge können ebenso verfahren.
Wenn der Drache rechnen kann, kann er immerhin dafür sorgen, dass er den obersten Zwerg essen kann, alle anderen muss er ausfliegen.
Für den Bonus bilden die Zwerge zuerst alle möglichen Hutfarbenfolgen. Zwei dieser Folgen werden äquivalent genannt, wenn sie sich nur an endlich vielen Stellen unterscheiden. Schließlich einigen sich die Zwerge (mittels des Auswahlaxioms) für jede Äquivalenzklasse auf einen Repräsentanten.
Stehen die Zwerge dann auf der Treppe, kann jeder einzelne, da er nur endlich viele Hüte nicht sieht, den Repräsentanten ihrer Hutfarbenfolge bestimmen. Danach können die Zwerge wie oben arbeiten, außer dass die Summen nur über die Hüte gebildet werden, die sich von dem Repräsentanten unterscheiden.
Damit kann der Drache höchstens den obersten Zwerg verspeisen.
Übrigens scheint auch der australische Youtuber mathologer unsere Rätsel zu lesen. Pünktlich im Januar hat er ein Video zu diesem Problem veröffentlicht.
"Liebe Gäste, lasst uns folgendes Spiel spielen. Da Ihr so gerne lustige Hüte aufsetzt, habe ich für euch blaue, rote und grüne Hüte vorbereitet. Jeder von Ihnen bekommt von mir einen dieser Hüte aufgesetzt (ohne dass er ihn sehen kann) und danach stellen Sie sich alle auf einer Treppe auf, sodass jeder nur die Hutfarbe der Zwerge sehen kann, die vor (und damit unter) ihm stehen. Danach darf jeder Zwerg, einer nach dem anderen in beliebiger Reihenfolge, seine Hutfarbe raten.
Die Zwerge, die ihre richtige Hutfarbe erraten, gewinnen einen Freiflug auf meinem Rücken. Die anderen werden zu einem schmackhaften Mittagessen zubereitet."
Die Zwerge erkennen den Ernst der Lage und bitten sich Bedenkzeit aus. Diese wird ihnen unter der Bedingung gewährt, dass der Drache die Beratung mit anhören darf, also in den Plan der Zwerge eingeweiht ist, um die Aufgabe so schwierig wie möglich machen zu können.
Mit welcher Strategie können möglichst viele Zwerge gerettet werden?
Diesmal hat der Drache sogar abzählbar viele Zwerge gefangen - und auch eine (nach unten) unendlich lange Treppe. Mit welcher Strategie können wieder möglichst viele Zwerge gerettet werden, wenn diese das Auswahlaxiom beherrschen?
Ellipsen im Einheitskreis - (Dezember 2016)
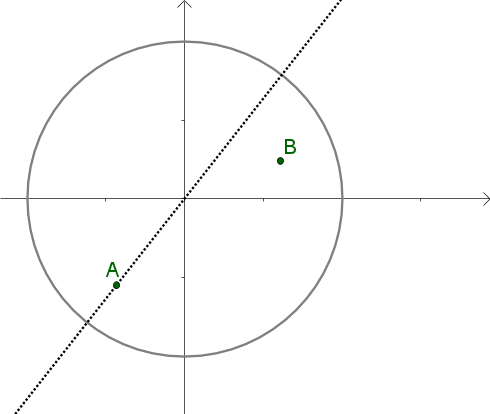
1. Möglichkeit:
Eine sehr anschaulich Lösung nimmt den Weg über die dritte Dimension.
Wir definieren Punkte \(x\), \(y\) und \(z\) auf der Einheitssphäre, deren Projektionen auf die Ebene gerade \(A\) bzw. \(B\) sind, also
\(x = \Big(A_1, A_2, \sqrt{1 - (A_1^2 + A_2^2)}\Big)\) und \(y = \Big(B_1, B_2, \sqrt{1 - (B_1^2 + B_2^2)}\Big)\), bzw. \(z = \Big(B_1, B_2, -\sqrt{1 - (B_1^2 + B_2^2)}\Big)\).
(Es reicht aus, nur zwei der vier Möglichkeiten zu betrachten.) Nun kann man sich leicht überlegen, dass es für die Punkte \(x,y\) bzw. \(x,z\) genau einen Großkreis, also einen zweidimensionalen Kreis auf der Kugeloberfläche mit Mittelpunkt im Ursprung, gibt, der durch beide Punkte verläuft. Werden diese Großkreise nun wieder in die zweidimensionale Ebene projiziert, erhalten wir die gesuchten Ellipsen. Anschaulich wird dies in dem Matlab/Octave-Skript ellipsen.m dargestellt. Dort findet man auch die genaue Darstellung der Ellipse.
2. Möglichkeit:
Für eine durch den Punkt \(A\) verlaufende Ellipse mit Mittelpunkt im Ursprung und großer Halbachsenlänge \(1\) sind die Brennpunkte von der Form \(F\), \(-F\) und es ist
\(|A-F|+|A-(-F)| = 2\),
(Stichwort: Gärtnerkonstruktion der Ellipse).
Das kann man aber umschreiben zu \(|F-A|+|F-(-A)| = 2\), das heißt \(F\) liegt auf der Ellipse \(E_A\) mit Brennpunkten \(A\) und \(-A\) und großer Halbachsenlänge \(1\). Analog finden wir eine Ellipse \(E_B\), auf der die Brennpunkte der Ellipsen liegen, die durch \(B\) verlaufen, den Mittelpunkt im Ursprung haben und große Halbachsenlänge \(1\) haben.
Die Brennpunkte der gesuchten Ellipsen durch \(A\) und \(B\) müssen also Schnittpunkte von \(E_A\) und \(E_B\) sein und davon gibt es nun einmal genau vier, also zwei Paare.
Man zeige, dass es genau zwei Ellipsen mit großer Halbachsenlänge \(1\) und Mittelpunkt im Ursprung gibt, die durch \(A\) und \(B\) verlaufen.

Alter der Kinder - (November 2016)

Zerlegt man \(72\) in Primfaktoren, so erhält man \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \). Probiert man nun die verschiedenen Möglichkeiten, die sich für die Alter der Kinder ergibt, gibt es nur eine Variante, sodass man die gleiche Zahl als Summe erhält: \( 2 + 6 + 6 = 14 = 3 + 3 + 8 \). Nur in diesem Fall kann Mathematiker B nicht sofort aus der Hausnummer auf die Alter der Kinder schließen.
Da aber ein Kind älter als die anderen ist, sind die Alter der Kinder schließlich \(3\), \(3\) und \(8\).
A: "Wie alt sind eigentlich deine drei Kinder?"
B: "Wenn man ihr Alter multipliziert, erhält man 72 und wenn man es addiert erhält man unsere Hausnummer."
A: "Das hilft mir jetzt aber noch nicht weiter."
B: "Das weiß ich. Aber mein ältestes Kind mag Schokokekse."
A: "Na dann weiß ich Bescheid!"
Wie alt sind die Kinder von Mathematiker B?
Durchmesser und Sehnen - (Oktober 2016)
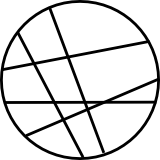

Über Zentralprojektion auf die Peripherie wird jede Sehne auf zwei gegenüberliegende Kreisbögen projiziert, welche beide länger sind, als die Sehne. Insbesondere Durchmesser haben als Bild den Vollkreis.
Zu unterschiedlichen Sehnen gehörende Kreisbögen schneiden sich genau in den Endpunkten von Durchmessern, die alle diese Sehnen treffen. Damit überdecken die Kreisbögen den Kreis höchstens \(k\) mal, ihre Gesamtlänge ist damit höchstens \(2 \pi k\). Folglich ist die Gesamtlänge der eingezeichneten Sehnen weniger als halb so groß, also kleiner als \(\pi k\).
Man beweise, dass die Summe der Längen aller eingezeichneten Sehnen kleiner als \(\pi k\) ist.
Rechteckproblem - (September 2016)
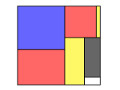
Eine sehr elegante beruht auf Integralrechnung: Wir betrachten die Funktion $$ f(x,y) = \sin(2 \pi x) \cdot \sin(2 \pi y) . $$ Wird diese Funktion über ein Rechteck integriert, dessen Seiten parallel zu \(x\)- und \(y\)-Achse liegen, dann ist das Integral null, wenn mindestens eine Seite des Rechtecks ganzzahlig ist. Dies hängt damit zusammen, dass das Integral in der Richtung der ganzzahligen Seitenläge nur volle Perioden der Sinusfunktion aufsammelt, und das Integral der Sinusfuntkion über eine Periode genau 0 ist.
Integriert man nun die Funktion \(f\) über ein großes Rechteck, welches aus vielen kleinen Rechtecken mit mindestens einer ganzzahligen Seite zusammengesetzt ist, dann addieren sich die Integrale über die einzelnen Rechtecke auf und das Gesamtintegral ist \(0\). Weiterhin können wir annehmen, dass das große Rechteck gerade \([0,a] \times [0,b]\) ist, also die linke, untere Ecke im Ursprung liegt. Eine kurze Rechnung zeigt dann $$ 0 = \int_0^a \int_0^b \sin(2 \pi x) \cdot \sin(2 \pi y) \, \mathrm{d}y \, \mathrm{d}x = \frac1{(2\,\pi)^2} \, ( \cos(2 \pi a) - \cos(0) ) \, ( \cos(2 \pi a) - \cos(b) ). $$ Dies bedeutet nun aber, dass mindestens eine Seite des Rechtecks ganzzahlig sein muss. Vierzehn weitere, verschiedene(!) Beweise findet man in dem Aufsatz Fourteen proofs of a Result About Tiling a Rectangle von Stan Wagon.
Beweise folgende Aussage:
Ein Rechteck, welches aus beliebig vielen Rechtecken mit mindestens einer ganzzahligen Seitenlänge zusammengesetzt werden kann, besitzt selbst wieder mindestens eine ganzzahlige Seitenlänge.
Hungriger Drache - (August 2016)

0=000000,
1=000001,
2=000010,
3=000011,
4=000100,
...,
61=111101,
62=111110,
63=111111.
Wir fangen hinten an: Wie ermittelt der Zwerg das Feld, auf das er zeigt? Ein Feld zu benennen heißt ja nach obiger Konvention, 6 Bits zu finden, und tun wir wie folgt:
Für das erste Bit zählen wir, wie viele der Wappen zeigenden Münzen bei ihrem ersten Bit 1 stehen haben. Ist diese Anzahl ungerade, so notieren wir 1 und ansonsten 0 für das erste Bit des Feldes, auf das gezeigt werden soll.
Für das zweite Bit verfahren wir analog mit den zweiten Bits der Wappen-Münzen, und ebenso mit den Bits 3 bis 6. Die so erhaltene Binärzahl gibt das Feld an, das der Zwerg bei der Frage nach dem Lieblingsfeld des Drachens rät.
Jetzt liegt es an der Zwergin, die Münzen auf dem Schachbrett so vorzubereiten, dass das errechnete Feld tatsächlich das Lieblingsfeld des Drachen ist. Dazu berechnet sie zunächst aus der originalen Münzkonfiguration des Drachen, auf welches Feld der Zwerg tippen würde und merkt sich die zugehörige Binärzahl. Dann schaut sie, welche Bits korrigiert werden müssen, damit das richtige Lieblingsfeld herauskommt. Diese Korrektur kann man durch das Umderehen der einen Münze erreichen, deren Binärzahl genau die noch falschen Bits gesetzt hat. Dreht man diese nämlich um, so ändert man genau bei den noch falschen Bits die Parität der 1-Bits bei den Wappenmünzen.
Auf diese Weise gewinnen die Zwerge den Freiflug mit 100%.
"Liebe Gäste, lasst uns folgendes Spiel spielen. Ich habe hier ein gewöhnliches 8×8 Schachbrett und 64 normale Münzen mit jeweils Wappen und Zahl. Die Zwergin begleitet mich nach nebenan, wo ich auf jedes Feld des Schachbrettes je eine Münze lege, und zwar je nach meinem Gutdünken mit Wappen oder Zahl oben. Dann suche ich mir mein Lieblingsfeld aus und zeige mit der Kralle darauf. Jetzt sucht sich die Zwergin sich eine Münze aus, die ich dann für sie umdrehe. Nun verlässt die Zwergin das Nebenzimmer durch einen zweiten Ausgang, und der Zwerg kommt herein. Wenn der Zwerg mir mein Lieblingsfeld nennen kann, dann gewinnt ihr einen Freiflug auf meinem Rücken und ich bringe euch, wohin ihr wollt. Falls nicht, gewinne ich und bereite euch zu meinem Mittagessen zu.".
Die Zwerge erkennen den Ernst der Lage und bitten sich Bedenkzeit aus. Diese wird ihnen unter der Bedingung gewährt, dass der Drache die Beratung mit anhören darf, also in den Plan der Zwerge eingeweiht ist, um die Aufgabe so schwierig wie möglich machen zu können.
Mit welcher Wahrscheinlichkeit können die Zwerge ihre Haut retten?
Dinge gibts, die gibts gar nicht! - (Juli 2016)

Mathematisch einsehen, dass es einen solchen Körper nicht geben kann, lässt sich dies gut an folgendem Bild:

Darin sind zwei Winkel rot markiert. Der eine ist ein Innenwinkel eines regelmäßigen Sechsecks und damit genau 120°. Der mit "?" markierte Winkel müsste nun, wenn man annimmt, dass die Fünfecke regelmäßig sind, aus Symmetriegründen ebenfalls 120° betragen.
Andererseits kann der mit "?" markierte Winkel nur dann 120° betragen, wenn die grüne und die blaue Dreiecksfläche parallel liegen (dies ist eine Aussage, die zwar plausibel ist, aber durchaus einen Beweis verdient, den wir hier der Übersichtlichkeit halber aber nicht ausführen).
Nun haben wir einen Widerspruch: Zwei benachbarte Dreiecks-Seitenflächen des vermeindlichen Johnson-Körpers müssten nach unseren Überlagungen parallel sein, (was sie augenscheinlich nicht sind). Wenn sie aber parallel sind, dann liegt kein Johnson-Körper mehr vor, denn die beiden Dreiecke würden dann zu einer rautenförmigen Seitenfläche zusammenfallen, welche kein regelmäßiges Polygon mehr ist.
Das sind strikt konvexe Polyeder, also Körper, deren Seitenflächen ausschließlich aus regelmäßigen Polygonen bestehen so dass zwei benachbarte Seitenflächen niemals in einer Ebene liegen. Bei platonischen Körpern müssen alle Seitenflächen und Winkel gleich sein, bei archimedischen verlangt man, dass noch eine besondere Art von Symmetrie vorliegt und der Rest sind Johnson-Körper.
Den Mathematikern sind seit langem alle platonischen, archimedischen und Johnson-Körper bekannt, siehe z.B. die Listen auf Wikipedia:
Platonische Körper
Archimedische Körper
Johnson-Körper .
Nun sind Bilder eines Körpers aufgetaucht, der zwölf Dreiecke, zwölf Fünfecke und zwei Sechsecke als Seitenflächen hat. Augenscheinlich ist er ein Johnson-Körper, aber er ist nicht in den obigen Listen zu finden. Das bedeutet, dass entweder die Mathematiker seit langem etwas übersehen haben oder dass wir euch gerade einen gewaltigen Bären aufbinden.
Was läuft hier schief?
Anti-Mersenne-Zahlen - (Juni 2016)
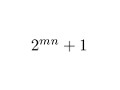
Es seinen m und n zwei ungerade natürliche Zahlen. Man zeige, dass 2mn+1 sowohl durch 2m+1 als auch durch 2n+1 teilbar ist.
Malen ohne Zahlen - (Mai 2016)

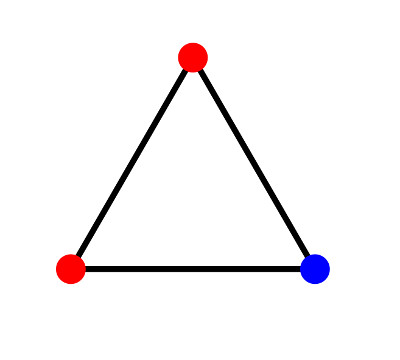
Im Fall, dass die Ebene mit drei Farben eingefärbt ist, kann man zum Beispiel ein etwas kompliziertes Gebilde von 7 Punkten, die so genannte Moser-Spindel aus dem Jahr 1961, betrachten, auf der immer zwei Punkte die gleiche Farbe haben müssen.
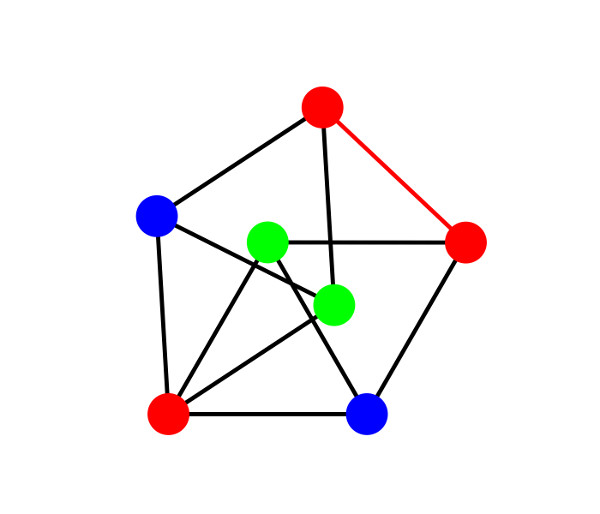
Leider ist das Problem im Fall von 4 Farben seit 1961 eine offene Frage (und die Frage nach der Zahl N sowieso).
Unsere dritte Aufgabe war also ein mathematisches Problem, für das noch keine Lösung bekannt ist. Geneigte Leser sind natürlich immer angehalten, nach Lösungen zu suchen.
Tatsächlich hat dieses Rätsel mit einem großen, offenen Problem der Mathematik zu tun, dem so genannten Hadwiger-Nelson-Problem:
Hadwiger-Nelson-Problem
Was ist die minimale Anzahl N an Farben, die nötig sind, um eine Ebene so einzufärben, so dass keine zwei Punkte im Abstand 1 die gleiche Farbe haben?
Die tatsächliche Zahl N ist also eine Zahl zwischen 4 und 7, wurde aber bis heute nicht genau identifiziert. Lediglich unter Zusatzannahmen wie "Lebesgue-Messbarkeit der Farbklassen" oder der Annahme, dass alle Zusammenhangskomponenten jeder Farbklasse konvexe Polygone sind, konnte gezeigt werden, dass N mindestens 5 bzw. mindestens 6 sein muss.
Man zeige: Es gibt immer zwei Punkte im Abstand von genau einem Zentimeter, die die gleiche Farbe haben.
Man zeige obige Aussage für den Fall, dass die Ebene in drei Farben angemalt ist.
Man zeige obige Aussage im Fall von vier Farben.
Verwirrungen auf dem Amt am 1. April - (April 2016)
Frage 1: "Welcher deiner Geschwister ist heute unzuverlässiger?"
- Wir haben den Ersten-April-Fanatiker gefragt. Der unzuverlässigere unter seinen zwei Brüdern an diesem Tag der April-Agnostiker und da der Fanatiker heute immer lügt, wird er auf den Ersten-April-Muffel zeigen.
- Wir haben den Ersten-April-Muffel gefragt. Der unzuverlässigere unter seinen zwei Brüdern ist an diesem Tag der April-Fanatiker. Also wird er auf diesen zeigen.
- Wir haben den Ersten-April-Agnostiker gefragt. Dann wird er auf irgendeinen Bruder zeigen.
Frage 2: "Würde der Bruder, der heute immer das Gegenteil von dem sagt, was du sagst, mir sagen, dass ich meinen neuen Reisepass heute NICHT abholen kann?"
- Wir haben den Fanatiker gefragt. Dieser wird uns anlügen und uns das Gegenteil der Wahrheit (das, was der Muffel sagen würde) mitteilen.
- Wir haben den Muffel gefragt. Dieser wird wahrheitsgemäß die Lüge, die der Fanatiker sagen würde, reproduzieren.
Nur am 1. April verhalten sie sich etwas sonderbar: Es ist stadtweit bekannt, dass ein Bruder (ein Erster-April-Fanatiker) an diesem Tag auf Ja-Nein-Fragen stets die falsche Antwort gibt. Ein zweiter (ein Erster-April-Muffel) antwortet stets korrekt und der dritte (ein Erster-April-Agnostiker) antwortet an diesem Tag nach Lust und Laune mal falsch und mal richtig.
Sie haben einen neuen Reisepass beantragt. Wie können Sie am 1. April mit nur zwei Ja-Nein-Fragen an je einen der drei Brüder herausfinden, ob der Pass schon abgeholt werden kann?
Zwergentanz - (März 2016)
Aus dieser Reihenfolge extrahiert er zwei Zahlen. Die erste berechnet er folgendermaßen. Er zählt, wie viele Zwerge vor ihm den ersten Raum betreten haben. Ist diese Zahl ungerade, merkt er sich -1, ansonsten merkt er sich +1. Die zweite Zahl ist das Signum der Permutation, die die anderen Zwerge von ihrer Reihenfolge beim Reinkommen aufsteigend nach ihren Losnummern sortiert. Das Produkt dieser zwei Zahlen entscheidet, welchen Schal man nimmt: rot bei -1 und weiß bei +1.
Warum funktioniert diese Startegie? Wir pfüfen sie zunächst für den Fall, dass die Losnummern aufsteigend verkauft wurden. In diesem Fall ist für jeden Zwerg die Sortierpermutation die Identität, und deren Signum ist +1. Wegen des abwechselnden Vorzeichens der ersten Zahl wechseln sich die Schalfarben im dritten Raum ab. Dieses positive Ergebnis möchten wir nun auf andere Losnummernreihenfolgen übertragen.
Dazu vergleichen wir die Ergebnisse zweier Losreihenfolgen, die sich nur in einer einzigen Transposition zweier aufeinanderfolgender Zwerge unterscheiden. Die beiden vertauschten Zwerge können keinen Unterschied erkennen, denn sie sehen ja nicht, wo sie selbst einsortiert sind. Ihr Signum bleibt also dasselbe, und damit auch ihre Schalfarbenwahl. Sie haben aber Platz getauscht, also sind die Schalfarben auf ihren Plätzen in der sortierten Aufstellung im dritten Raum vertauscht. Glücklicherweise sehen alle anderen Zwerge die Transposition. Dadurch wechselt ihr Signum das Vorzeichen und sie wählen allesamt die jeweils andere Schalfarbe, so dass das Ergebnis im dritten Raum zwar genau umgekehrt aber ebenso zum Gewinnen taugt ist wie vorher.
Nun kann man jede Reihenfolge der Losnummern mit Hilfe von Transpositionen von Nachbarn von der Identität aus erreichen. Also führen alle Losnummernreihenfolgen ebenso wie die Identität zum Erfolg der Strategie. Am Signum der Permutation, die alle Zwerge auf einmal sortiert, kann man übrigens ablesen, welche der beiden Gewinnkonfigurationen eintreten wird, aber diese Information ist den Zwergen natürlich erst im dritten Raum zugänglich.
Die Verlosung läuft folgendermaßen ab: Jeder Zwerg kauft ein Los. Das Los wird so an der Zwergenmütze befestigt, dass der Träger die Losnummer nicht sehen kann. Die Losnummern sind reelle Zahlen, und keine Zahl wird zweimal verkauft. Im ersten Raum kann sich jeder Zwerg die Losnummern der anderen Teilnehmer anschauen. Von dort aus geht es einzeln weiter in den zweiten Raum, wo jeder Zwerg wählen muss, ob er einen roten oder einen weißen Schal mit in den dritten Raum nimmt. Im dritten Raum dürfen die Teilnehmer dann endlich ihre Losnummer ansehen und müssen sich aufsteigend nach Losnummern sortieren. Gewonnen hat die ganze Gruppe, wenn im dritten Raum keine zwei Teilnehmer mit gleicher Schalfarbe nebeneinander stehen.
Natürlich darf in den Räumen eins und zwei nicht kommuniziert werden.
Wie können die Zwerge in dieser Lotterie gewinnen?
Pfannkuchen essen - (Februar 2016)

Das lässt sich wie folgt einsehen: Wir stellen uns vor, dass die beiden zunächst abwechselnd Pfannkuchen vom großen Berg nehmen und auf ihren Teller legen bis der große Berg Pfannkuchen in der Mitte abgetragen ist. Dann essen sie abwechselnd je einen Pfannkuchen. Dieses Vorgehen ist äquivalent (die Wahrscheinlichkeiten, den falschen Pfannkuchen zu essen ändern sich nicht) und natürlich verliert derjenige, auf dessem Teller der Ekelpfannkuchen liegt. Allerdings liegen bei ungeradem n auf Klaus Teller ein Pfannkuchen mehr, womit die Wahrscheinlichkeit, dass er den falschen erwischt höher ist als die von Kalle.
Zu Hause können die beiden an den Pfannkuchen keine äußerlichen Unterschiede feststellen. Die einzige Möglichkeit, den falschen zu identifizieren, ist hineinzubeißen. So machen sie ein Spiel daraus: Abwechselnd isst jeder einen Krapfen und sobald einer den Scherzpfannkuchen erwischt hat, hat er verloren.
Kalle lässt Klaus den Vortritt und denkt: "Soll der mal anfangen, vielleicht erwischt er ja gleich beim ersten Versuch den falschen!"
Klaus ist schon ein Jahr älter und kennt sich mit Wahrscheinlichkeiten aus. Er denkt: "Es ist besser, wenn ich anfange! Die Wahrscheinlichkeit, dass ich beim ersten Versuch den Ekelpfannkuchen erwische ist doch winzig klein. Da hat der Kalle ein höheres Risiko, wenn er in den zweiten beißen muss, denn ich habe dann ja schon den ersten guten Pfannkuchen weggegessen."
Beide wissen, dass man das auch ausrechnen könnte, aber hey, einen Berg Pfannkuchen aufzuessen macht einfach zu viel Spaß!
Wer von den beiden hat die schlechtere Strategie gewählt?
Das heißt, wer hat das größere Risiko, den Chili-Senf-Knoblauchmayonnaisepfannkuchen zu erwischen?
Kreissehnen - (Januar 2016)
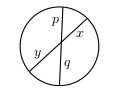
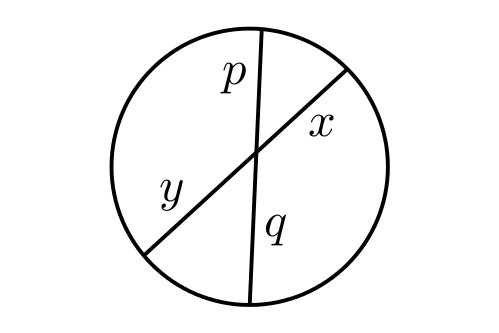
In einem Kreis haben zwei Sehnendreiecke mit gleicher Sehne im dieser Sehne gegenüberliegenden Punkt denselben Winkel.
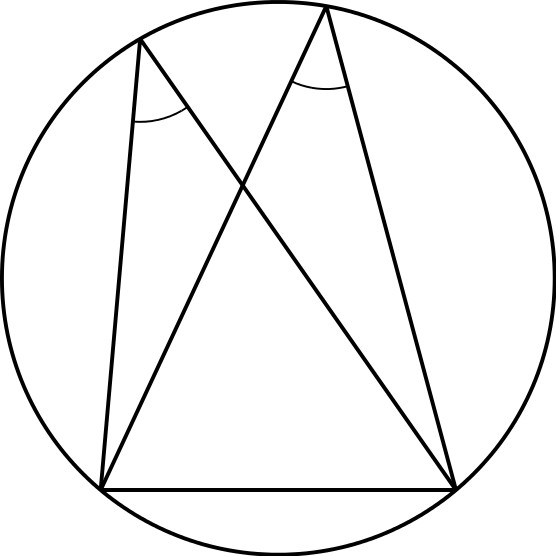
Also sind die gleich markierten Winkel im folgenden Bild gleich groß, denn sie sind über derselben (jeweils gepunkteten) Sehne im Kreis abgetragen.
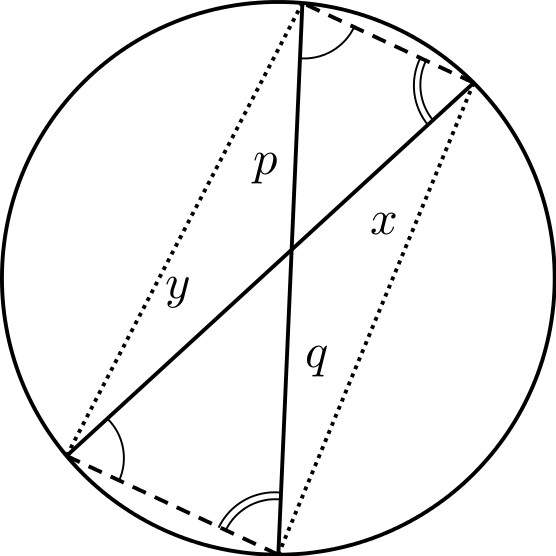
Deshalb sind die Dreiecke, die sich im Schnittpunkt der durchgezogenen Sehnen gegenüberliegen und durch je eine gestrichelte Linie berandet werden, ähnlich. Daher gilt x/p=q/y beziehungsweise xy=pq.
Man zeige: \(xy=pq\).
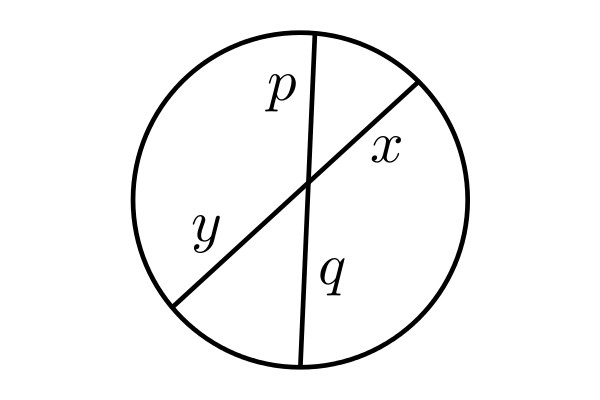
Der algebraische Kalender - (Weihnachten 2015)

Christian setzt zunächst einmal auf die fleißige Lösungsvariante und will alle Möglichkeiten ausschöpfen. Er beginnt damit, die Eins nach oben (“auf 12 Uhr”) zu setzen und setzt probeweise eine andere Zahl rechts daneben (“auf 1 Uhr”).
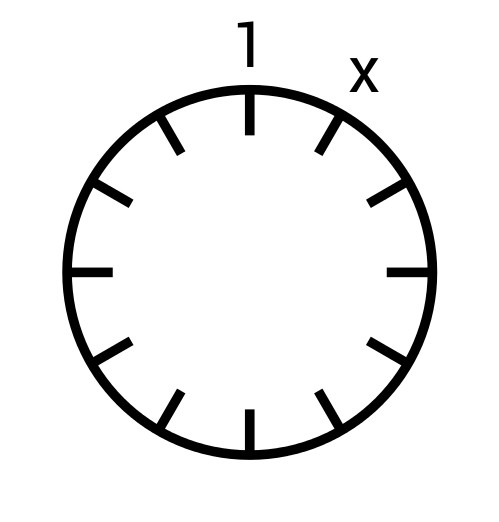
Nun stellt sich ein überraschender Effekt ein: alleine durch diese zwei Einträge ist die komplette Uhr determiniert. Jede Zahl ist durch ihre beiden Vorgänger und die Gleichung b2 = a · c (mod 13) bestimmt. Christian muss nur oft probieren und nachdem er das 13er Einmaleins auswendig gelernt hat kann er für alle Werte von x die Uhr füllen.
Allerdings erreicht Christian nicht immer alle zwölf Zahlen. So beobachtet er manchmal eine Abfolge von vier Zahlen, die sich dreimal wiederholt.
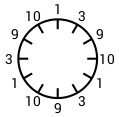
So etwas ist natürlich nicht zulässig, da ja alle zwölf Zahlen vorkommen müssen! Nach langem Ausprobieren hat Christian genau vier passenden Anordnungen gefunden.
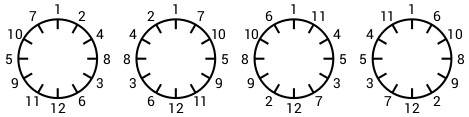
Da er die Eins auf zwölf Uhr festgelegt hatte, kann er jeden dieser vier Kalender noch um 12 verschiedene Winkel rotieren. Also gibt es 48 geeignete Anordnungen.
Manche werden es erkannt haben: da steckt natürlich mehr dahinter, als bloses Ausprobieren. Das Rechnen modulo 13 ist deshalb spannend, weil man hier wieder eine Division hat (Mathematiker sagen, dass die Ganzen Zahlen modulo 13 einen Körper ergeben). Das bedeutet, dass jede Zahl x zwischen 1 und 12 (die 0 ist wie immer ausgenommen) über ein multiplikatives Inverses x-1 verfügt, also eine Zahl, so dass x · x-1 = 1 (mod 13).
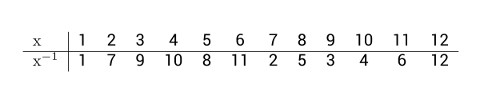
Solche multiplikativen Inversen gibt es übrigens immer beim Rechnen modulo p, solange p eine Primzahl ist. Noch anders ausgedrückt, rechnen wir in der “zwölfelementigen Gruppe der invertierbaren Elemente in ZZ mod 13”, aber das würde hier etwas zu weit führen ...
Nun können wir die Gleichung b2 = a · c (mod 13) umstellen zu c = b2 · a-1 (mod 13) und uns durchhangeln. Wir sehen, dass die Uhr wie folgt aufgebaut sein muss:
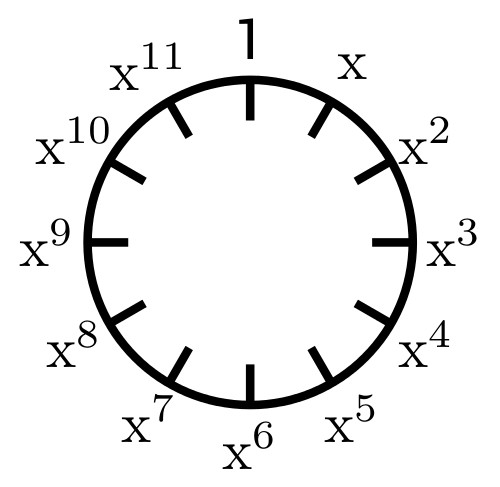
Es scheint also zu genügen, eine Zahl zwischen eins und zwölf zu wählen und Potenzen dieser Zahl modulo dreizehn zu berechnen. Allerdings erzeugt nicht jedes Zahl x zwischen Eins und Zwölf die komplette Gruppe, sondern eben nur die vier oben genannten Kandidaten. Man könnte hier nun wieder anfangen, etwas über Untergruppen zu erzählen, aber wir wollen ja nicht übertreiben ...
Zuletzt kann man sich noch fragen, wieso wir genau vier Möglichkeiten haben und nicht zum Beispiel drei oder sechs: auch das lässt sich anschaulich erklären: mit Symmetrien! Ist ein die Gruppe erzeugendes Element, sagen wir 2, gegeben, so sind es auch 2-1=7 (mod 13), -2 = 11 (mod 13) und (-2)-1 = 11-1 = 6 (mod 13) und das sind eben vier Elemente.
a2 = b · c (mod 13)
(Der Ausdruck ``mod 13'' bedeutet, dass auf jeder Seite der Gleichung der Rest beim Teilen durch 13 betrachtet wird.)
Flächeninhalt von Dreiecken - (Dezember 2015)
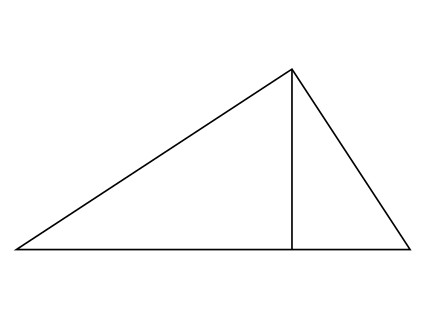
Die Hypothenuse eines rechtwinkligen Dreiecks misst 10 Zentimeter, und die dazu senkrechte Höhe misst 6 Zentimeter. Man ermittele den Flächeninhalt.
Fehlersuche - (November 2015)

N · p = 12,
N · q = 16 und
N · pq = 8.
Die Lösung dieses Gleichungssystems ist N = 24, p = 1/2 und q = 2/3. Im Text befanden sich also geschätzt 24 Fehler. Davon wurden 12 + 8 = 20 entdeckt, also besagt unsere Schätzung, dass sich noch 4 Fehler in der Arbeit verstecken.
Schätze, wie viele unentdeckte Fehler sich noch in Caros Arbeit verstecken!