Erstellung von Graphiken mittels Matplotlib, Seaborn und Plotly#
Matplotlib ist eine mächtige Python-Bibliothek, welche viele Funktionen für die graphische Darstellung in Form von Plots und Diagrammen bereitstellt. Wir werden in diesem Abschnitt die grundlegende Funktionsweise kennenlernen. Sehr viele neuere Graphik-Pakete bauen auf diesem Basispaket auf und erleichtern die Erstellung von Graphiken oder erweitern den Funktionsumfang. So können mit Plotly, welches Bestandteil des Matplotlib-Pakets ist, interaktive Graphiken erstellt werden und mit Seaborn insbesondere klassiche statistische Plots sehr komfortabel erstellt werden. Wir starten mit dem Basis-Paket Matplotlib und stellen am Ende einen Beispieldatensatz mit allen drei Paketen dar, um die Unterschiede beim Erzeugen aufzuzeigen.
Visualisierung mit Matplotlib#
Erste Schritte#
Ähnlich wie bei NumPy müssen wir Matplotlib und Seaborn erst installieren. Dies erledigt man in seiner Conda-Umgebung mit folgendem Befehl:
conda install -c conda-forge matplotlib
conda install -c conda-forge seaborn
Anschließend können wir Matplotlib, besser gesagt das Submodul matplotlib.pyplot in unser Programm einbinden:
import matplotlib.pyplot as plt
Der wichtigste Befehl ist plt.plot(...). Wir geben plt.plot? ein um zu erfahren wie dieser funktioniert. In der einfachsten Form sind die Argumente dieser Funktion 2 Vektoren mit \(x\)- bzw. \(y\)-Koordinaten einer Punktwolke. Diese Vektoren können Listen, oder Numpy-Arrays sein. Die Sinusfunktion können wir wie folgt plotten:
import numpy as np
x = np.linspace(0, 2*np.pi, 11) # Erzeuge Gitter [0, 0.2*pi, 0.4*pi, ..., 2*pi])
y = np.sin(x) # Berechne zugehörige Funktionswerte
plt.plot(x,y) # Erzeuge Plot
plt.show() # Zeige den Plot
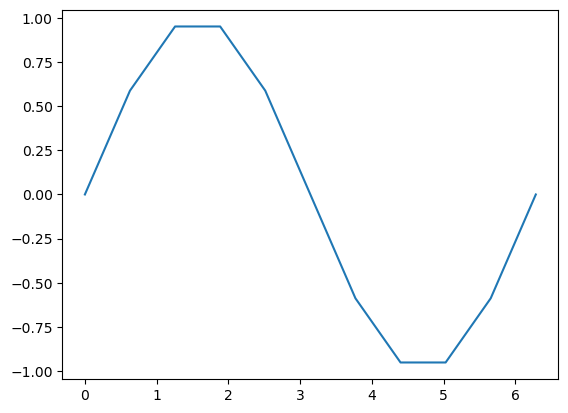
Hier sehen wir auch eine schöne Anwendung der komponentenweise definierten mathematischen Funktionen aus numpy.
Übungsaufgabe
Plotte die Funktion \(f(x) = e^{-x}\,\sin(2\,\pi\,x)\) im Intervall \([0,6]\).
Gestaltung von Plots#
Machen wir unseren Plot noch etwas schöner:
import numpy as np
x = np.linspace(0,4*np.pi, 1001) # Erzeuge äquidistantes Gitter für das Intervall [0, 4*pi]
y = np.sin(x) # Berechne zugehörige Funktionswerte für sinus
z = np.cos(x) # und cosinus
plt.figure(figsize=(10,5)) # Größe einstellen
plt.plot(x,y,label="$\sin(x)$") # Erzeuge Plot für Sinus
plt.plot(x,z,label="$\cos(x)$") # Erzeuge Plot für Cosinus
plt.title("Sinus und Cosinus") # Titel des Plots
plt.grid() # Gitterlinien einschalten
plt.xlabel('x') # Bezeichner an x-Achse
plt.ylabel('f(x)') # Bezeichner an y-Achse (in Latex-Code)
plt.legend() # Legende
plt.show() # Zeige den Plot
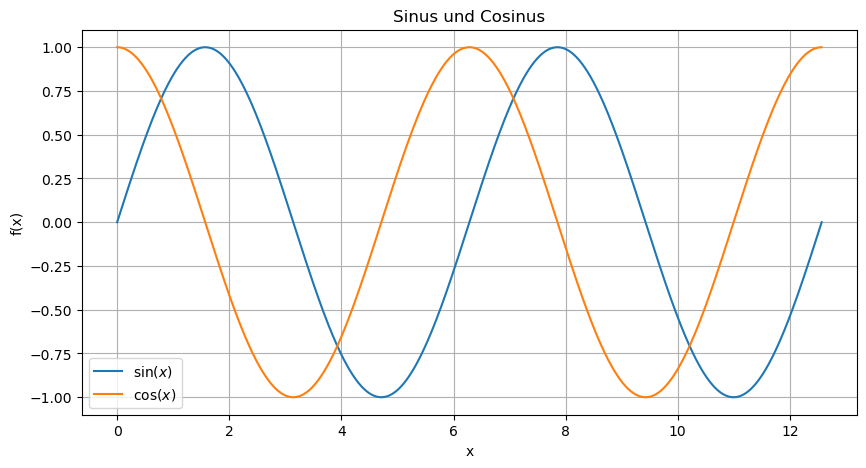
Im Prinzip hat Matplotlib unsere Punktwolke mit Koordinaten aus x und y gezeichnet, und die Punkte mit Linen verbunden. Es gibt aber noch einige andere Linientypen:
x = np.linspace(0,2,21)
y1= x-0.5*x**2
y2= 2*x-x**2
y3= 3*x-1.5*x**2
plt.figure(figsize=(10,5)) # Größe einstellen
# Zeichne rote (r) Kreise (o) mit Verbindungslinien (-)
plt.plot(x, y1, 'ro-', linewidth=0.2, label='f1')
# Zeichne blaue (b) Quadrate (s)
plt.plot(x, y2, 'bs', label='f1')
# Zeichne cyane (c) Dreiecke (^) mit gestrichelten Verbindungslinien (--)
plt.plot(x, y3, 'c^--', markersize=10, label='f1')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()
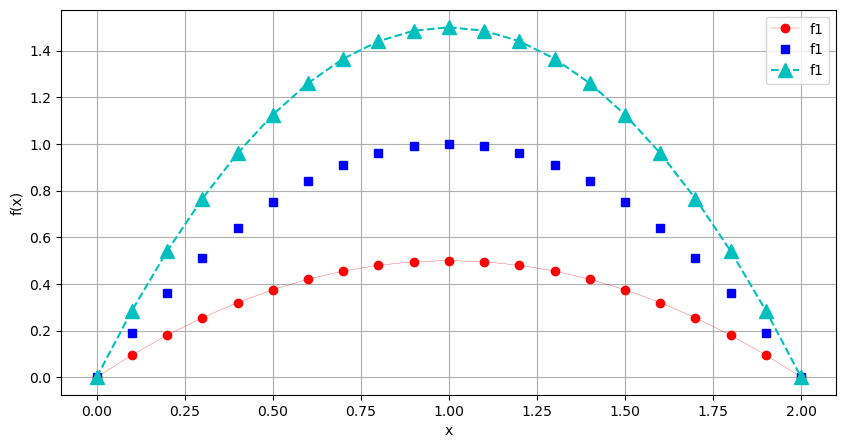
Im Hilfetext plt.plot? sind noch weitere Linien- und Markertypen erklärt. Vordefinierte Farben im Submodul matplotlib.colors. Es gibt verschiedene Farbpaletten. Die Grundfarben sind:
import matplotlib.colors as mcolors
mcolors.BASE_COLORS
{'b': (0, 0, 1),
'g': (0, 0.5, 0),
'r': (1, 0, 0),
'c': (0, 0.75, 0.75),
'm': (0.75, 0, 0.75),
'y': (0.75, 0.75, 0),
'k': (0, 0, 0),
'w': (1, 1, 1)}
Es gibt weiterhin die Farbpalette Tableau:
mcolors.TABLEAU_COLORS
{'tab:blue': '#1f77b4',
'tab:orange': '#ff7f0e',
'tab:green': '#2ca02c',
'tab:red': '#d62728',
'tab:purple': '#9467bd',
'tab:brown': '#8c564b',
'tab:pink': '#e377c2',
'tab:gray': '#7f7f7f',
'tab:olive': '#bcbd22',
'tab:cyan': '#17becf'}
Und außerdem noch CSS-Farben:
mcolors.CSS4_COLORS
{'aliceblue': '#F0F8FF',
'antiquewhite': '#FAEBD7',
'aqua': '#00FFFF',
'aquamarine': '#7FFFD4',
'azure': '#F0FFFF',
'beige': '#F5F5DC',
'bisque': '#FFE4C4',
'black': '#000000',
'blanchedalmond': '#FFEBCD',
'blue': '#0000FF',
'blueviolet': '#8A2BE2',
'brown': '#A52A2A',
'burlywood': '#DEB887',
'cadetblue': '#5F9EA0',
'chartreuse': '#7FFF00',
'chocolate': '#D2691E',
'coral': '#FF7F50',
'cornflowerblue': '#6495ED',
'cornsilk': '#FFF8DC',
'crimson': '#DC143C',
'cyan': '#00FFFF',
'darkblue': '#00008B',
'darkcyan': '#008B8B',
'darkgoldenrod': '#B8860B',
'darkgray': '#A9A9A9',
'darkgreen': '#006400',
'darkgrey': '#A9A9A9',
'darkkhaki': '#BDB76B',
'darkmagenta': '#8B008B',
'darkolivegreen': '#556B2F',
'darkorange': '#FF8C00',
'darkorchid': '#9932CC',
'darkred': '#8B0000',
'darksalmon': '#E9967A',
'darkseagreen': '#8FBC8F',
'darkslateblue': '#483D8B',
'darkslategray': '#2F4F4F',
'darkslategrey': '#2F4F4F',
'darkturquoise': '#00CED1',
'darkviolet': '#9400D3',
'deeppink': '#FF1493',
'deepskyblue': '#00BFFF',
'dimgray': '#696969',
'dimgrey': '#696969',
'dodgerblue': '#1E90FF',
'firebrick': '#B22222',
'floralwhite': '#FFFAF0',
'forestgreen': '#228B22',
'fuchsia': '#FF00FF',
'gainsboro': '#DCDCDC',
'ghostwhite': '#F8F8FF',
'gold': '#FFD700',
'goldenrod': '#DAA520',
'gray': '#808080',
'green': '#008000',
'greenyellow': '#ADFF2F',
'grey': '#808080',
'honeydew': '#F0FFF0',
'hotpink': '#FF69B4',
'indianred': '#CD5C5C',
'indigo': '#4B0082',
'ivory': '#FFFFF0',
'khaki': '#F0E68C',
'lavender': '#E6E6FA',
'lavenderblush': '#FFF0F5',
'lawngreen': '#7CFC00',
'lemonchiffon': '#FFFACD',
'lightblue': '#ADD8E6',
'lightcoral': '#F08080',
'lightcyan': '#E0FFFF',
'lightgoldenrodyellow': '#FAFAD2',
'lightgray': '#D3D3D3',
'lightgreen': '#90EE90',
'lightgrey': '#D3D3D3',
'lightpink': '#FFB6C1',
'lightsalmon': '#FFA07A',
'lightseagreen': '#20B2AA',
'lightskyblue': '#87CEFA',
'lightslategray': '#778899',
'lightslategrey': '#778899',
'lightsteelblue': '#B0C4DE',
'lightyellow': '#FFFFE0',
'lime': '#00FF00',
'limegreen': '#32CD32',
'linen': '#FAF0E6',
'magenta': '#FF00FF',
'maroon': '#800000',
'mediumaquamarine': '#66CDAA',
'mediumblue': '#0000CD',
'mediumorchid': '#BA55D3',
'mediumpurple': '#9370DB',
'mediumseagreen': '#3CB371',
'mediumslateblue': '#7B68EE',
'mediumspringgreen': '#00FA9A',
'mediumturquoise': '#48D1CC',
'mediumvioletred': '#C71585',
'midnightblue': '#191970',
'mintcream': '#F5FFFA',
'mistyrose': '#FFE4E1',
'moccasin': '#FFE4B5',
'navajowhite': '#FFDEAD',
'navy': '#000080',
'oldlace': '#FDF5E6',
'olive': '#808000',
'olivedrab': '#6B8E23',
'orange': '#FFA500',
'orangered': '#FF4500',
'orchid': '#DA70D6',
'palegoldenrod': '#EEE8AA',
'palegreen': '#98FB98',
'paleturquoise': '#AFEEEE',
'palevioletred': '#DB7093',
'papayawhip': '#FFEFD5',
'peachpuff': '#FFDAB9',
'peru': '#CD853F',
'pink': '#FFC0CB',
'plum': '#DDA0DD',
'powderblue': '#B0E0E6',
'purple': '#800080',
'rebeccapurple': '#663399',
'red': '#FF0000',
'rosybrown': '#BC8F8F',
'royalblue': '#4169E1',
'saddlebrown': '#8B4513',
'salmon': '#FA8072',
'sandybrown': '#F4A460',
'seagreen': '#2E8B57',
'seashell': '#FFF5EE',
'sienna': '#A0522D',
'silver': '#C0C0C0',
'skyblue': '#87CEEB',
'slateblue': '#6A5ACD',
'slategray': '#708090',
'slategrey': '#708090',
'snow': '#FFFAFA',
'springgreen': '#00FF7F',
'steelblue': '#4682B4',
'tan': '#D2B48C',
'teal': '#008080',
'thistle': '#D8BFD8',
'tomato': '#FF6347',
'turquoise': '#40E0D0',
'violet': '#EE82EE',
'wheat': '#F5DEB3',
'white': '#FFFFFF',
'whitesmoke': '#F5F5F5',
'yellow': '#FFFF00',
'yellowgreen': '#9ACD32'}
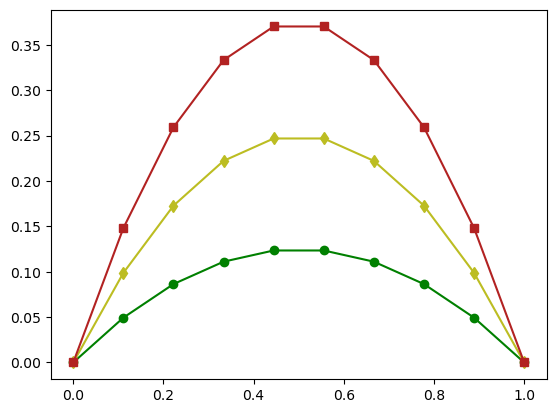
Durch Setzen des Parameters color im Plot-Befehl kann nun eine Farbe aus einer der oberen Farbpaletten gewählt werden:
x = np.linspace(0,1,10)
plt.plot(x,0.5*x*(1-x),'o-',color='g') # Grundfarbe
plt.plot(x,x*(1-x),'d-',color='tab:olive') # Tableau-Farbe
plt.plot(x,1.5*x*(1-x),'s-',color='firebrick') # CSS-Farbe
plt.show()
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
def plot_colortable(colors, title, sort_colors=True, emptycols=0):
cell_width = 212
cell_height = 22
swatch_width = 48
margin = 12
topmargin = 40
# Sort colors by hue, saturation, value and name.
if sort_colors is True:
by_hsv = sorted((tuple(mcolors.rgb_to_hsv(mcolors.to_rgb(color))),
name)
for name, color in colors.items())
names = [name for hsv, name in by_hsv]
else:
names = list(colors)
n = len(names)
ncols = 4 - emptycols
nrows = n // ncols + int(n % ncols > 0)
width = cell_width * 4 + 2 * margin
height = cell_height * nrows + margin + topmargin
dpi = 72
fig, ax = plt.subplots(figsize=(width / dpi, height / dpi), dpi=dpi)
fig.subplots_adjust(margin/width, margin/height,
(width-margin)/width, (height-topmargin)/height)
ax.set_xlim(0, cell_width * 4)
ax.set_ylim(cell_height * (nrows-0.5), -cell_height/2.)
ax.yaxis.set_visible(False)
ax.xaxis.set_visible(False)
ax.set_axis_off()
ax.set_title(title, fontsize=24, loc="left", pad=10)
for i, name in enumerate(names):
row = i % nrows
col = i // nrows
y = row * cell_height
swatch_start_x = cell_width * col
text_pos_x = cell_width * col + swatch_width + 7
ax.text(text_pos_x, y, name, fontsize=14,
horizontalalignment='left',
verticalalignment='center')
ax.add_patch(
Rectangle(xy=(swatch_start_x, y-9), width=swatch_width,
height=18, facecolor=colors[name], edgecolor='0.7')
)
return fig
plot_colortable(mcolors.BASE_COLORS, "Grundfarben",
sort_colors=False, emptycols=1)
plot_colortable(mcolors.TABLEAU_COLORS, "Tableau-Palette",
sort_colors=False, emptycols=2)
plot_colortable(mcolors.CSS4_COLORS, "CSS-Farben")
# Optionally plot the XKCD colors (Caution: will produce large figure)
# xkcd_fig = plot_colortable(mcolors.XKCD_COLORS, "XKCD Colors")
# xkcd_fig.savefig("XKCD_Colors.png")
plt.show()



Bei der Fehleranalyse sind oft logarithmische Achsen von interesse. Angenommen, wir analysieren einen iterativen Algorithmus und messen die Entfernung \(\text{err}_n\) zwischen exakter Lösung und der berechnete Näherungslösung nach \(n\) Iterationen. Man sagt, das Verfahren konvergiert
Q-linear, falls \(\text{err}_n \le C\, \text{err}_{n-1}\) mit \(C\in (0,1)\)
Q-superlinear, falls \(\text{err}_n \le \varepsilon_n\,\text{err}_{n-1}\) mit einer Nullfolge \(\varepsilon_n\searrow 0\)
Q-quadratisch, falls \(\text{err}_n \le C\, \text{err}_{n-1}^2\) mit \(C>0\).
Stellen wir den Fehlerverlauf in einem kartesischen Koordinatensystem und einem Koordinatensystem mit logarithmischer \(y\)-Achse dar:
import math
n = np.array(range(1,6), dtype='float64')
err_p1 = (0.8)**n
err_p2 = [1./math.factorial(int(i)) for i in n]
err_p3 = (0.8)**(2**n)
plt.figure(figsize=(10,5))
def generate_plot():
plt.plot(n, err_p1, 'ro-', label='Q-linear')
plt.plot(n, err_p2, 'bo-', label='Q-superlinear')
plt.plot(n, err_p3, 'co-', label='Q-quadratisch')
plt.grid()
# Plot in kartesischen Koordinatensystem
plt.subplot(1,2,1)
generate_plot()
plt.legend(loc='upper right')
# Plot in Koordinatensystem mit logarithmischer y-Achse
plt.subplot(1,2,2)
generate_plot()
plt.semilogy()
plt.legend(loc='lower left')
plt.show()
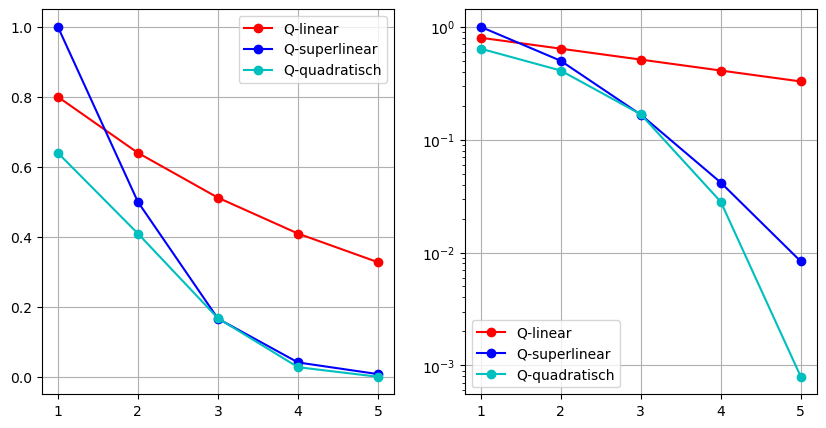
Wir sehen, dass eine \(Q\)-linear konvergente Folge im Plot mit logarithmischer \(y\)-Achse einer lineare Funktion ist.
Analog dazu kann man auch die \(x\)-Achse mit plt.semilogx() logatithmisch skalieren, was bei oben vorgestellter Anwendung allerdings wenig Sinn macht.
Balken-, Linien- und Kuchendiagramme#
Schauen wir uns weitere elementare Plot-Typen an. Angenommen wir haben die Auswertung einer Umfrage vorliegen, und möchten diese graphisch aufbereiten. Unsere Beispieldaten sind:
parties = ["CDU", "SPD", "FDP", "Grüne", "Linke", "AfD", "Sonstige"]
colors = ["black", "red", "yellow", "green", "violet", "blue", "gray"]
values = [25.3, 26.3, 13.9, 14.2, 6.2, 4.9]
values.append(100-sum(values))
Wir können anstelle des plot-Befehls auch stem verwenden um ein Liniendiagramm zu erstellen, scatter für ein Streudiagramm, bar für ein Balkendiagramm oder pie für ein Tortendiagramm. Im folgenden Beispiel werden die Unterschiede gezeigt:
plt.figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.stem(parties, values)
plt.title("Plot")
plt.subplot(2,2,2)
plt.bar(parties, values, color=colors)
plt.title("Bar")
plt.subplot(2,2,3)
plt.scatter(parties, values, color=colors)
plt.title("Scatter")
plt.subplot(2,2,4)
plt.pie(values, labels=parties, explode=[0,0.2,0,0.2,0,0,0], colors=colors)
plt.title("Pie")
plt.show()
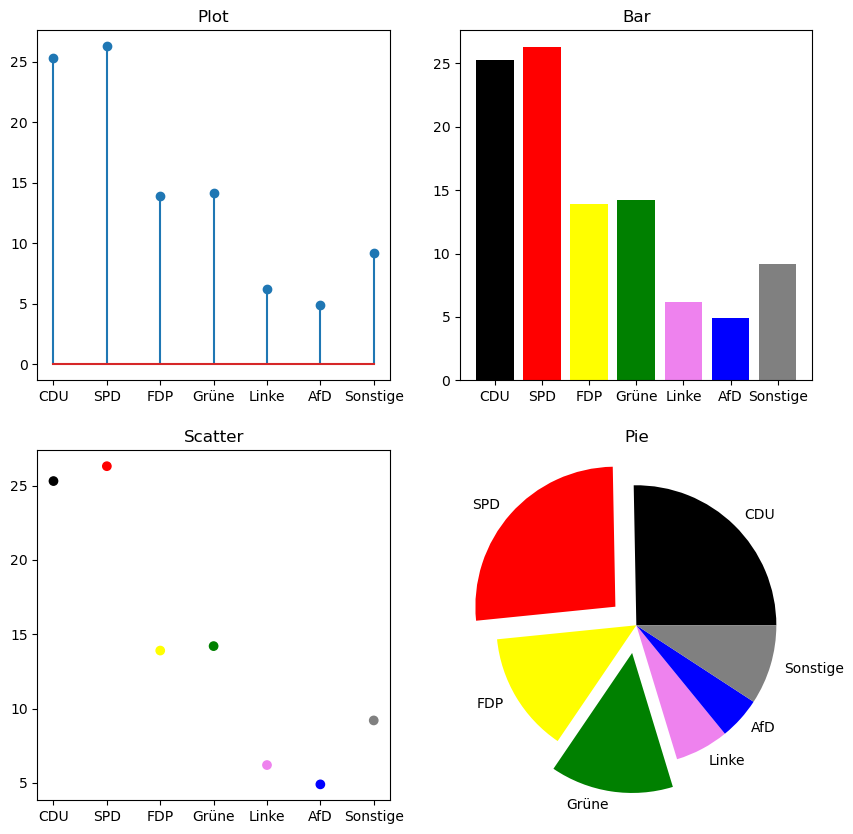
Error-Bars#
Eine u.U. angenehme Methode für Visualisierungen ist der Error-Bar, da dieser grafisch die Standardabweichung zu einem bestimmten (Zeit-)Punkt darstellt. Der nachfolgende Code demonstriert die einmal.
Für die Datumskonvertierung finden Sie unter den nachfolgenden Verlinkungen Hilfe 1, 2 und 3.
import pandas as pd
Kurs_ALV=pd.read_csv("/Users/erwinjentzsch/finance-python/Data/Allianz_Schlusskurse_2020_2025.csv", header=1) # To-Do: Anpassen; header = csv beginnt in Spalte eins nicht mit Kurs und Datum, sondern mit Ticker.
Kurs_ALV = Kurs_ALV.rename(columns={"Ticker": "Datum", "ALV.DE": "Schlusskurs"}) #Spaltenbeschriftungen umbennen
Kurs_ALV = Kurs_ALV.drop(0).reset_index(drop=True) #Erste Zeile rauswerfen --> drop(0); Mit .reset_index(drop=True) wird der Index neu durchnummeriert (0, 1, 2, …); Sonst bleibt der alte Index erhalten und wir beginnen mit Index 1
### Datum konvertieren
Kurs_ALV["Datum"] = pd.to_datetime(Kurs_ALV["Datum"], errors="coerce") # errors="coerce": ersetzt ungültige Werte durch NaT (bei Datumswerten) bzw. NaN (bei Zahlen); mithilfe von errors==coerce" gehen wir sicher, dass alle Werte in der Spalte in ein Datumformat konvertiert worden sind. Alternativ errors=ignore oder errors=raise
# Halbjahr bilden und aggregieren
Kurs_ALV["Quartal"] = Kurs_ALV["Datum"].dt.to_period("1Q")
gruppen = Kurs_ALV.groupby("Quartal")["Schlusskurs"]
mittel = gruppen.mean()
std = gruppen.std()
## Erstellung error-bar
fig, ax = plt.subplots(figsize=(10,5)) # Diagramm vergrößern (Breite=10 Zoll, Höhe=5 Zoll)
ax.errorbar(
mittel.index.astype(str), # Achtung, wir haben mit mittel.index keine Zahl o.ä. Matplotlib kann PeriodIndex nicht direkt verarbeiten, da wir Jahr+Quartal haben (Benutzerdefiniert). Wir müssen hier als den Index in einen String umwandeln.
mittel.values,
yerr=std.values,
marker="o",
linestyle="-",
color="b",
)
ax.set_title("Allianz – Schlusskurse je Quartal")
ax.set_ylabel("Kurs")
plt.tight_layout() # Passt das Layou des Diagramms automatisch an.
plt.xticks(rotation=45)
plt.show()
---------------------------------------------------------------------------
FileNotFoundError Traceback (most recent call last)
Cell In[13], line 3
1 import pandas as pd
----> 3 Kurs_ALV=pd.read_csv("/Users/erwinjentzsch/finance-python/Data/Allianz_Schlusskurse_2020_2025.csv", header=1) # To-Do: Anpassen; header = csv beginnt in Spalte eins nicht mit Kurs und Datum, sondern mit Ticker.
6 Kurs_ALV = Kurs_ALV.rename(columns={"Ticker": "Datum", "ALV.DE": "Schlusskurs"}) #Spaltenbeschriftungen umbennen
7 Kurs_ALV = Kurs_ALV.drop(0).reset_index(drop=True) #Erste Zeile rauswerfen --> drop(0); Mit .reset_index(drop=True) wird der Index neu durchnummeriert (0, 1, 2, …); Sonst bleibt der alte Index erhalten und wir beginnen mit Index 1
File ~/miniconda3/envs/finance/lib/python3.11/site-packages/pandas/io/parsers/readers.py:1026, in read_csv(filepath_or_buffer, sep, delimiter, header, names, index_col, usecols, dtype, engine, converters, true_values, false_values, skipinitialspace, skiprows, skipfooter, nrows, na_values, keep_default_na, na_filter, verbose, skip_blank_lines, parse_dates, infer_datetime_format, keep_date_col, date_parser, date_format, dayfirst, cache_dates, iterator, chunksize, compression, thousands, decimal, lineterminator, quotechar, quoting, doublequote, escapechar, comment, encoding, encoding_errors, dialect, on_bad_lines, delim_whitespace, low_memory, memory_map, float_precision, storage_options, dtype_backend)
1013 kwds_defaults = _refine_defaults_read(
1014 dialect,
1015 delimiter,
(...)
1022 dtype_backend=dtype_backend,
1023 )
1024 kwds.update(kwds_defaults)
-> 1026 return _read(filepath_or_buffer, kwds)
File ~/miniconda3/envs/finance/lib/python3.11/site-packages/pandas/io/parsers/readers.py:620, in _read(filepath_or_buffer, kwds)
617 _validate_names(kwds.get("names", None))
619 # Create the parser.
--> 620 parser = TextFileReader(filepath_or_buffer, **kwds)
622 if chunksize or iterator:
623 return parser
File ~/miniconda3/envs/finance/lib/python3.11/site-packages/pandas/io/parsers/readers.py:1620, in TextFileReader.__init__(self, f, engine, **kwds)
1617 self.options["has_index_names"] = kwds["has_index_names"]
1619 self.handles: IOHandles | None = None
-> 1620 self._engine = self._make_engine(f, self.engine)
File ~/miniconda3/envs/finance/lib/python3.11/site-packages/pandas/io/parsers/readers.py:1880, in TextFileReader._make_engine(self, f, engine)
1878 if "b" not in mode:
1879 mode += "b"
-> 1880 self.handles = get_handle(
1881 f,
1882 mode,
1883 encoding=self.options.get("encoding", None),
1884 compression=self.options.get("compression", None),
1885 memory_map=self.options.get("memory_map", False),
1886 is_text=is_text,
1887 errors=self.options.get("encoding_errors", "strict"),
1888 storage_options=self.options.get("storage_options", None),
1889 )
1890 assert self.handles is not None
1891 f = self.handles.handle
File ~/miniconda3/envs/finance/lib/python3.11/site-packages/pandas/io/common.py:873, in get_handle(path_or_buf, mode, encoding, compression, memory_map, is_text, errors, storage_options)
868 elif isinstance(handle, str):
869 # Check whether the filename is to be opened in binary mode.
870 # Binary mode does not support 'encoding' and 'newline'.
871 if ioargs.encoding and "b" not in ioargs.mode:
872 # Encoding
--> 873 handle = open(
874 handle,
875 ioargs.mode,
876 encoding=ioargs.encoding,
877 errors=errors,
878 newline="",
879 )
880 else:
881 # Binary mode
882 handle = open(handle, ioargs.mode)
FileNotFoundError: [Errno 2] No such file or directory: '/Users/erwinjentzsch/finance-python/Data/Allianz_Schlusskurse_2020_2025.csv'
Plots für Skalar- und Vektorfelder#
Auch für die graphische Darstellung von Skalarfeldern \(f\colon \mathbb{R}^2 \to \mathbb{R}\) und Vektorfeldern \(\vec F\colon \mathbb{R}^2 \to \mathbb{R}^2\) stehen einige Funktionen in Matplotlib bereit. Die meisten Funktionen zur Darstellung von Skalarfeldern erwarten als Argument 3 Matrizen, eine für die \(x\)-Koordinaten, eine für die \(y\)-Koordinaten und eine für den Funktionswert \(f(x,y)\). Hilfreich ist hier die Funktion numpy.meshgrid mit der wir ein 2D-Tensorprodukt-Gitter aus 2 1D-Gittern erzeugen:
# 1D-Gitter für x- und y-Variable
x = np.linspace(-4.5,3.5,1001)
y = np.linspace(-3.5,3.5,1001)
# 2D-Gitter erzeugen
X,Y = np.meshgrid(x,y)
# Definiere Himmelblau-Funktion
Z = (X**2 + y - 11)**2 + (X + Y**2 - 7)**2
Eine mögliche Darstellung einer solchen Funktion wäre ein Contour-Plot, in welchem die Kurven \(\{(x,y)\colon f(x,y)=c_i\}\) für verschiedene Werte \(c_1<c_2 < \ldots<c_{\text{levels}}\) eingezeichnet werden:
plt.contour(X,Y,Z, levels=25)
plt.colorbar()
plt.show()
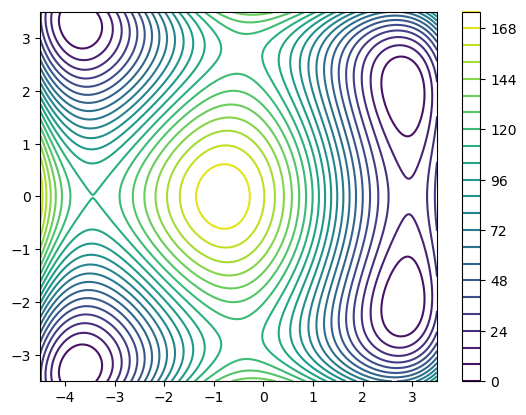
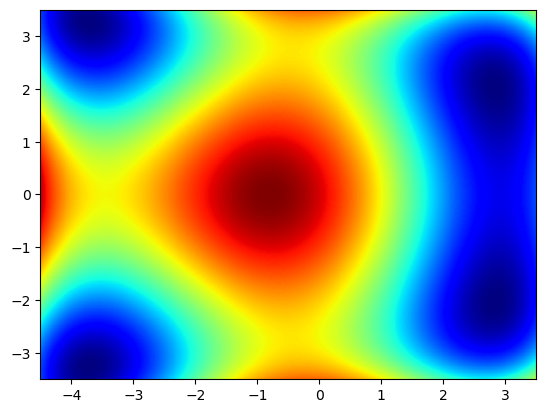
Ähnlich funktionieren Color-Plots, bei denen der Funktionswert an einer Stelle \((x,y)\) dem Farbwert einer vordefinierten Farbpalette entspricht:
import matplotlib.cm as cm
plt.pcolormesh(X,Y,Z, cmap=cm.jet)
plt.show()
Skalarfelder lassen sich auch in dreidimensionalen Koordinatensystemen darstellen. Die Argumente werden auf \(x\)- und \(y\)-Achse aufgetragen, und der Funktionswert auf die \(z\)-Achse. Die entsprechenden Plot-Befehle sind allerdings nicht im Submodul matplotlib.pyplot definiert, daher müssen wir einen Umweg nehmen. Zunächst erzeugen wir uns ein Bildobjekt mit
fig = plt.figure()
fügen ein 3D-Koordinatensystem hinzu
ax = fig.axes(projection='3d')
und nutzen die vom Objekt ax bereitgestellten Plot-Befehle. Hier ein Beispiel:
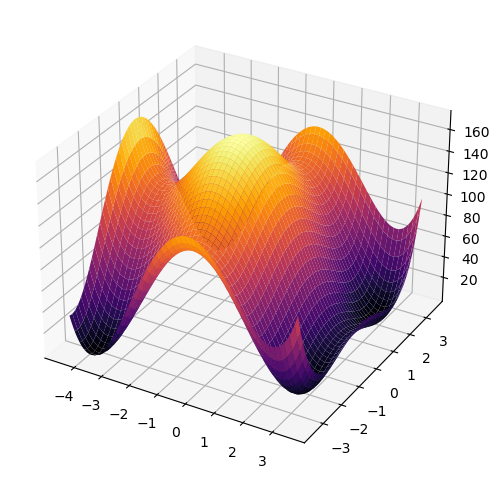
plt.figure(figsize=(8,6))
# 3D-Koordinatensystem hinzufügen
ax = plt.axes(projection='3d')
# Surface-Plot erstellen
ax.plot_surface(X,Y,Z, cmap=cm.inferno)
plt.show()
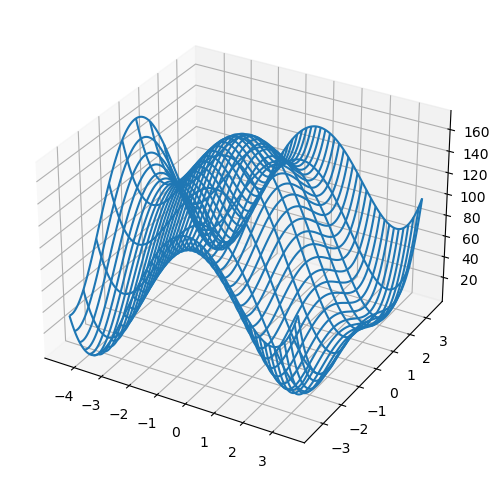
plt.figure(figsize=(8,6))
ax = plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z, rcount=10)
plt.show()
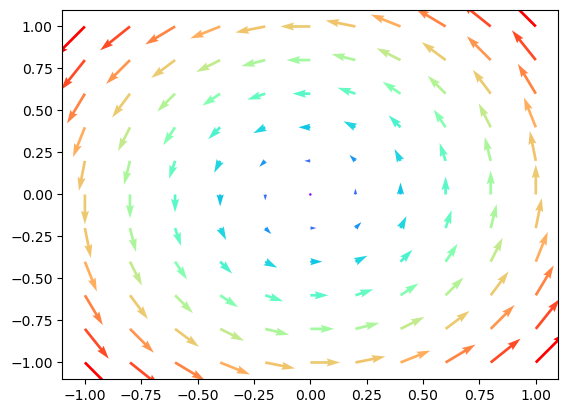
Schauen wir uns noch eine Methode mit der wir Vektorfelder zeichnen können. Als Beispiel definieren wir \(\vec f(x,y) = (-y,x)^\top\). Solche Vektorfelder können in sogenannten Quiver-Plots dargestellt werden:
x = np.linspace(-1,1, 11)
y = np.linspace(-1,1, 11)
# Punktgitter definieren
X,Y = np.meshgrid(x, y)
# Funktionswerte von F
Z1 = -Y
Z2 = X
# Optional: Färbe Pfeile nach Länge
C = np.sqrt(Z1**2 + Z2**2)
# Quiverplot erzeugen und anzeigen
plt.quiver(X, Y, Z1, Z2, C, cmap=cm.rainbow)
plt.show()
Auch Kurven lassen sich in Matplotlib zeichnen. Eine Kurve ist zunächst eine Menge an Punkten
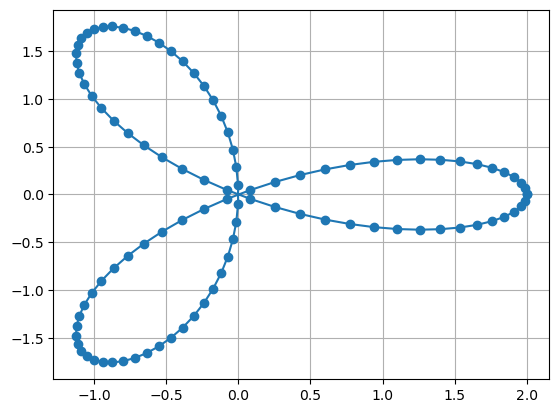
mit einer sogenannten Kurvenparametrisierung \(\vec x\colon[t_a,t_b]\to\mathbb{R}^n\), welche regulär ist, d.h., \(\dot{\vec x}(t)\ne 0\) für alle \(t\in [t_a,t_b]\). Für eine ebene Kurve (\(n=2\)) können wir den normalen Plot-Befehl nutzen. Das Kleeblatt
zeichnen wir beispielsweise mit
t = np.linspace(0,2*np.pi,100)
x = np.cos(t)+np.cos(2*t)
y = np.sin(t)-np.sin(2*t)
plt.plot(x,y,'o-')
plt.grid()
plt.show()
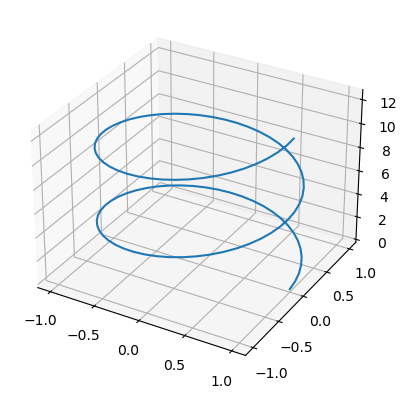
Ähnlich kann man Raumkurven (\(n=3\)) zeichnen, man benötigt nur vorher ein dreidimensionales Koordinatensystem. Wie wir das anlegen haben wir aber schon gesehen. Wir zeichnen hier die Schraubenlinie
t = np.linspace(0,4*np.pi,100)
x = np.cos(t)
y = np.sin(t)
z = t
ax = plt.axes(projection='3d')
ax.plot3D(x, y, z)
plt.show()
Graphiken mit Seaborn - to do#
Interaktive Graphiken mit Plotly - to do#
Vergleich der Graphik-Pakete Matplotlib, Seaborn und Plotly#
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.io as pio
import plotly.express as px
import plotly.offline as py
import pandas as pd
import numpy as np
np.random.seed(42) #initialisiere Zufallsgenerator für reproduzierbare "Zufallsdaten"
#pio.renderers.default = "plotly_mimetype"
#pio.renderers.default = "browser"
pio.renderers.default = "notebook" # oder "notebook_connected" für interaktive Version
Erzeugen uns Daten mit Funktionswerten von sin(x) und cos(x), zufällig gestört mit etwas normalverteilten Rauschen
# Beispieldaten erzeugen
x = np.linspace(0, 10, 50)
y1 = np.sin(x) + np.random.normal(scale=0.1, size=len(x))
y2 = np.cos(x) + np.random.normal(scale=0.1, size=len(x))
df = pd.DataFrame({
"x": np.concatenate([x, x]),
"y": np.concatenate([y1, y2]),
"Function": ["sin"]*len(x) + ["cos"]*len(x)
})
df
| x | y | Function | |
|---|---|---|---|
| 0 | 0.000000 | 0.049671 | sin |
| 1 | 0.204082 | 0.188842 | sin |
| 2 | 0.408163 | 0.461693 | sin |
| 3 | 0.612245 | 0.727009 | sin |
| 4 | 0.816327 | 0.705219 | sin |
| ... | ... | ... | ... |
| 95 | 9.183673 | -1.117426 | cos |
| 96 | 9.387755 | -0.969703 | cos |
| 97 | 9.591837 | -0.959973 | cos |
| 98 | 9.795918 | -0.931403 | cos |
| 99 | 10.000000 | -0.862530 | cos |
100 rows × 3 columns
type(df)
pandas.core.frame.DataFrame
df ist ein DataFrame im Tidy-Format, siehe beispielsweise tidy-format
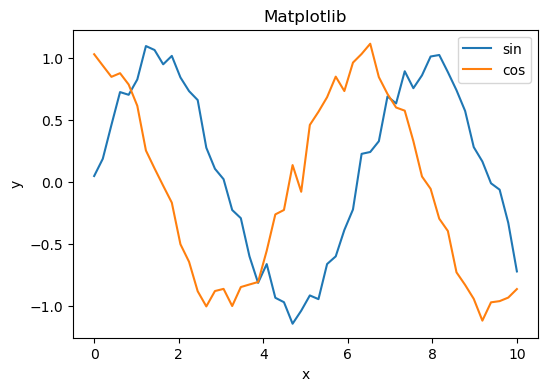
# --- Matplotlib ---
plt.figure(figsize=(6,4))
for func in df["Function"].unique():
subset = df[df["Function"] == func]
plt.plot(subset["x"], subset["y"], label=func)
plt.title("Matplotlib")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
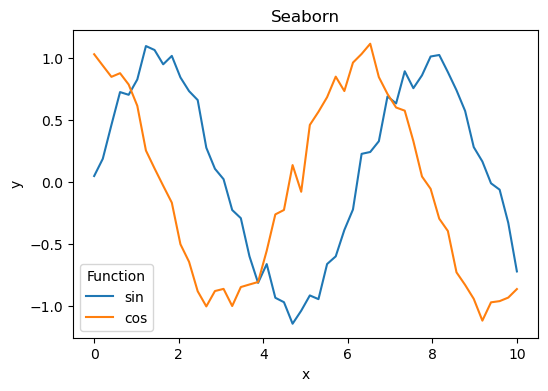
# --- Seaborn ---
plt.figure(figsize=(6,4))
sns.lineplot(data=df, x="x", y="y", hue="Function")
plt.title("Seaborn")
plt.show()
# --- Plotly ---
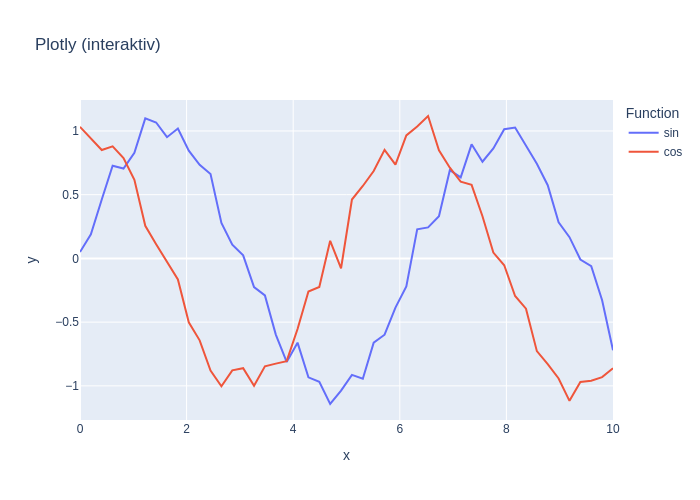
fig = px.line(df, x="x", y="y", color="Function", title="Plotly (interaktiv)")
fig.show()
fig.write_image("plotly_bsp.png")
Die Interaktion ist insbesondere in Browsern sinnvoll. Fährt man nun mit dem Mauszeiger über die Graphen, erhält man Infos über die Datenwerte angezeigt oder kann in die Graphiken hinein- oder herauszoomen. Klinckt man in die Legende, können einzelne Funktionen ausgeschaltet werden.
Achtung: Plotly nicht für pdf-Version von jupyter-notebook verfügbar – daher wird hier die interaktive Graphik in eine Bilddatei umgewandlet und als Alternative hier eingebunden: