9. Risikomaße (Entwurf)

In diesem Abschnitt beschäftigen wir uns mit Risikomaßen. Für unsere Notationen und Ausführungen greifen wir auf die Kapitel 4-6 aus dem Vorlesungsskript: Portfolio Optimization von Herrn Prof. Dr. Pichler zurück.

9.1. Definition (Verteilungsfunktion)

Sei \(Y : \Omega \rightarrow \mathbb{R}\) eine reellwertige Zufallsvariable. Die Verteilungsfunktion ist definiert als: \(F_Y(x) := P(Y \leq x)\).

9.2. Definition (Value-at-Risk)

Der Value-at-Risk zum Konfidenzniveau \(\alpha \in [0,1]\) ist definiert durch:

\(\text{V@R}_\alpha(Y) := F_Y^{-}(\alpha) = \inf \left\{ x: P(Y \leq x) \geq \alpha \right\}\)

Der Value-at-Risk ist auch bekannt als Quantilsfunktion \(q_\alpha(Y) := \text{V@R}_\alpha(Y)\) oder verallgemeinerte Inverse.

Bemerkung: Für weitere Informationen zum V@R verweisen wir an dieser Stelle auf Kapitel 4 aus dem Vorlesungsskript: Portfolio Optimization.

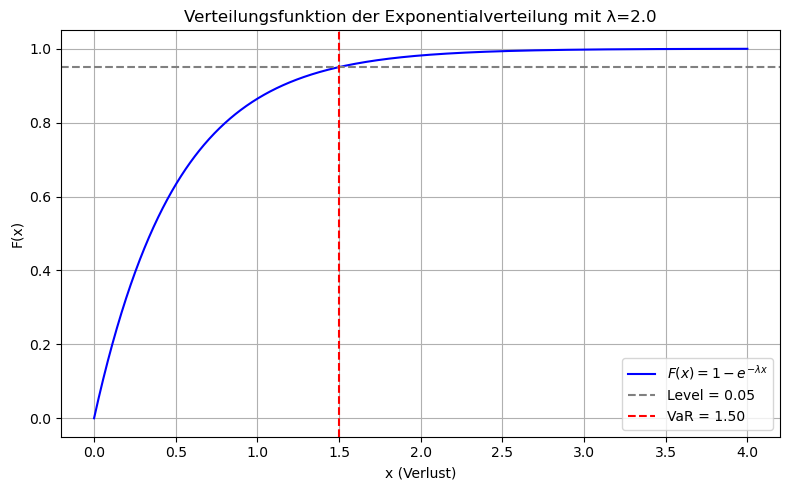
Wir möchten nun die Quantilsfunktion an einem Beispiel berechnen. Sei \(X \sim {Exp}(\lambda)\) mit der Verteilungsfunktion

\[\begin{split} F(x) = \int_0^x f_\lambda(t)\,\mathrm{d}t = \begin{cases} 1 - e^{-\lambda x}, & x > 0, \\ 0, & x \leq 0. \end{cases} \end{split}\]

Des weiteren setzen wir \(\alpha=0.95\).

import numpy as np
from scipy.stats import norm

lmbda = 2              
alpha = 0.95
conf = 1-alpha   # Konfidenzniveau

Die verallgemeinerte Inverse der Exponentialverteilung stimmt der gewöhnlichen Inversen \(F^{-1}\) überein, d.h. es gilt \(F^{-1}(u)=F^-(u)=-\frac{ln(1-u)}{\lambda}\).

# Verallgemeinerte Inverse berechnen 
var = - (1 / lmbda) * np.log(1-alpha)

# Gerundet auf Zwei-Nachkommastellen
print(f"Der V@R beträgt: {var:.5f}.")

Der V@R beträgt: 1.49787.

Der folgende Code erzeugt Grafiken zur Illustration

import numpy as np
import matplotlib.pyplot as plt

# x-Werte und CDF
x = np.linspace(0, 4, 1000)
cdf = 1 - np.exp(-lmbda * x)

# Plot
plt.figure(figsize=(8, 5))

# Verteilungsfunktion zeichnen
# Ein raw string (r'$F(x) = 1 - e^{-\lambda x}$') behandelt Backslashes (\) nicht als Escape-Zeichen.
plt.plot(x, cdf, label=r'$F(x) = 1 - e^{-\lambda x}$', color='blue')

# Konfidenzniveau (horizontale Linie): 
#plt.axhline(conf_level, color='grey', linestyle='--', label=f'Konfidenzniveau = {alpha:.2f}')
plt.axhline(alpha, color='grey', linestyle='--', label=f'Level = {conf:.2f}')

# VaR (vertikale Linie)
plt.axvline(var, color='red', linestyle='--', label=f'VaR = {var:.2f}')

# Beschriftung und Layout
plt.title(f"Verteilungsfunktion der Exponentialverteilung mit λ={lmbda:.1f}")
plt.xlabel('x (Verlust)')
plt.ylabel('F(x)')
plt.legend()
plt.grid(True)
plt.tight_layout()

# Plot anzeigen
plt.show()

alpha_vals = np.linspace(0.01, 0.99, 200)

# Quantilfunktion (VaR_alpha) für die Exponentialverteilung
VaR_alpha = -np.log(1 - alpha_vals) / lmbda

# Grafik erstellen
plt.figure(figsize=(6,4))
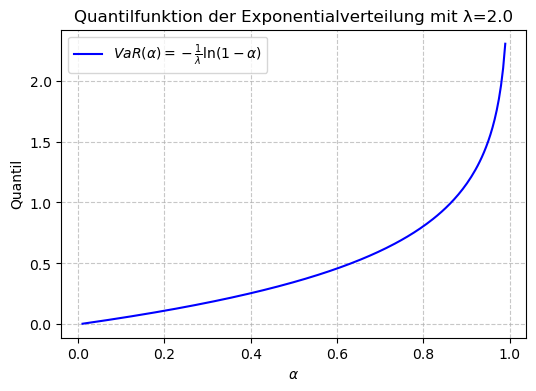
plt.plot(alpha_vals, VaR_alpha, label=r'$VaR(\alpha) = -\frac{1}{\lambda}\ln(1-\alpha)$', color='blue')
plt.xlabel(r'$\alpha$')
plt.ylabel('Quantil')
plt.title(f"Quantilfunktion der Exponentialverteilung mit λ={lmbda:.1f}")
#plt.title(' Exponentialverteilung (λ={lmbda:.2f})')
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.show()

# {avar:.5f}

9.3. Definition Average Value-at-Risk

Der AV@R zum Niveau Niveau \(\alpha \in [0,1]\) ist wie folgt definiert:

\[\text{AV@R}_\alpha(Y):=\frac{1}{1-\alpha}\int_\alpha^1 \text{ V@R}_p(Y)dp=\frac{1}{1-\alpha}\int_\alpha^1 F_Y^-(u)du \quad \text{ für} \quad 0\leq\alpha < 1\]

und für \(\alpha=1\)

\[\text{AV@R}_1(Y):=ess \text{ } sup \text{ } Y\]

Bemerkung: Der Average Value-at-Risk wird auch Conditional Value-at-Risk sowie Conditional Tail Expection (CTE), Expected Shortfall, Tail Value-at-Risk oder Super-Quantile bezeichnet. Für weitere Informationen zum AV@R verweisen wir an dieser Stelle auf den Gliederungspunkt 6.2 aus dem Vorlesungsskript: Portfolio Optimization.

# AVaR mit definierter Quantilsfunktion der Exponentialverteilung
from scipy.integrate import quad
def integrand(u):
    return - (1 / lmbda) * np.log(1 - u) 

# [0] = gibt den numerischen Wert der Integrals zurück
# [1] = gibt zusätzlich den Fehler wieder (Das Integral wird approximiert) 
avar = (1 / (1 - alpha)) * quad(integrand, alpha, 1)[0]
print(f"Der AV@R für die Exponentialverteilung bei einem alpha von {alpha} beträgt: {avar:.5f}")

#Theorie: AVaR_α = E[X | X > VaR_α] = VaR_α + 1/λ, to do: wo ist der Fehler???  

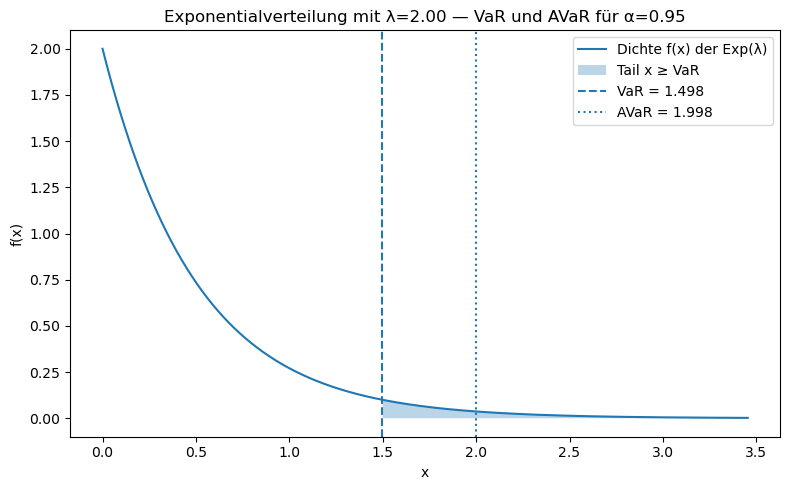
Der AV@R für die Exponentialverteilung bei einem alpha von 0.95 beträgt: 1.99787

Weitere Informationen zum Subpackage scipy.integrate finden Sie hier.

Für die Exponentialverteilung kann das Integral über die Quantilfunktion auch einfach berechnet werden:

\[ \text{AV@R}_\alpha(Y)=\frac{1}{1-\alpha}\int_\alpha^1 \left( - \frac 1\lambda \log(1-u) \right) du = \frac 1\lambda - \frac 1\lambda \log(1-\alpha) = \frac 1 \lambda + \text{V@R}_\alpha \]

avar = var + 1/lmbda

# --- Grid for the pdf plot ---
q_999 = -np.log(1 - 0.999) / lmbda
x = np.linspace(0, q_999, 1000)
pdf = lmbda * np.exp(-lmbda * x)

# --- Plot ---
fig = plt.figure(figsize=(8, 5))
plt.plot(x, pdf, label="Dichte f(x) der Exp(λ)")
# Shade the tail beyond VaR_α
mask = x >= var
plt.fill_between(x[mask], pdf[mask], alpha=0.3, label=f"Tail x ≥ VaR")

# Vertical lines for VaR and AVaR
plt.axvline(var, linestyle="--", label=f"VaR = {var:.3f}")
plt.axvline(avar, linestyle=":", label=f"AVaR = {avar:.3f}")

# Labels, legend, title
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title(f"Exponentialverteilung mit λ={lmbda:.2f} — VaR und AVaR für α={alpha:.2f}")
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()

# Print numeric values
var, avar

(1.497866136776995, 1.997866136776995)