8. Regressionsmodelle#
In diesem Kapitel werden wir uns ausführlich mit Regressionsmodellen als grundlegendes Werkzeuge der quantitativen Analyse beschäftigen. Ziel ist es, sowohl das theoretische Verständnis linearer Modelle zu vermitteln als auch deren praktische Umsetzung in Python zu beherrschen. Dazu erarbeiten wir zunächst die statistischen Grundlagen und implementieren einfache und multiple lineare Regressionen Schritt für Schritt mit NumPy, bevor wir anschließend die Ansätze etablierter Statistik-Bibliotheken wie statsmodels oder scikit-learn kennenlernen.
Für den Einstieg betrachten wir die Konstruktion einer einfachen Regressionsgeraden, um das Prinzip der Parameterschätzung und der Fehlerquadratsumme anschaulich zu verstehen, und verallgemeinern diese Überlegungen dann auf höherdimensionale Modelle. Aufbauend darauf beschäftigen wir uns mit statistischen Tests auf Regressionskoeffizienten, Konfidenzintervallen und Modellgüte sowie mit ANOVA-Konzepten, die helfen, Modelle systematisch zu bewerten.
Literatur: beispielsweise [8], [9] oder [10]
Abschließend widmen wir uns Anwendungen im Bereich der Finanzzeitreihen. Dabei stehen insbesondere die Voraussetzungen klassischer Regressionsmodelle im Vordergrund – vor allem die Annahme unabhängiger Beobachtungen – und welche Besonderheiten bei abhängigen Daten wie Rendite-Reihen beachtet werden müssen.
8.1. Motivation: Bestimmung der Regressionsgeraden#
Scatterplots, wie im folgenden Beispiel, stellen den Zusammenhang zwischen zwei metrischen Merkmalen \(X\) und \(Y\) dar. Mit Hilfe von Regressionsmodellen, versucht man die Werte von \(Y\) mit Hilfe von Beobachtungen \(X\) durch Analyse der Stichprobenpaare \((x_1,y_1), \ldots, (x_n,y_n)\) vorherzusagen. Das einfachste Modell
unterstellt einen linearen Zusammenhang zwischen \(X\) und \(Y\), wobei \(E\) ein zufälliges Rauschen ohne Tendenz (\(\mathbb{E} E = 0\)) diesen streng funktionellen Zusammenhang etwas aufweicht. Den Fehlerterm bzw. Rauschterm \(E\) bezeichnet man daher auch als Residuen. Ein allgemeines Modell \(Y = f(X) + E\) unterstellt einen funktionalen Zusammenhang zwischen \(X\) und \(Y\), der mit Hilfe der Funktion \(f\) beschrieben wird. In obigen Modell ist die Funktion \(f\) einfach linear mit \(f(x)=a+bx\), wir können allerdings auch eine quadratische Funktion \(f(x)=a+bx +cx^2\) anpassen. Allgemein bezeichnet
\(Y ...\) Regressand / abhängige bzw. zu erklärende Variable, d.h. \(Y\) wird mittels \(X\) erklärt
\(X ...\) Regressor / unabhängie bzw. erklärende Variable (häufig deterministisch modelliert)
wobei \(X\) durchaus auch mehrdimensional sein darf. Das folgende Beispiel stellt den Zusammenhang zwischen Rechnung und Trinkgeldern dar. Der Scatterplot zeigt einen positiven Zusammenhang, je höher die Gesamtrechnung, desto höher auch die gezahlten Trinkgelder.
import seaborn as sns
import matplotlib.pyplot as plt
# tips-Datensatz (Restaurant-Trinkgelder) aus seaborn package
tips = sns.load_dataset("tips")
print(tips.head())
#univariate statistische Kennzahlen
print(tips.describe())
# einfache lineare Regression: Trinkgeld ~ Gesamtrechnung
sns.lmplot(data=tips, x="total_bill", y="tip", ci=None)
plt.title("Lineare Regression: Tip ~ Total Bill")
plt.show()
total_bill tip sex smoker day time size
0 16.99 1.01 Female No Sun Dinner 2
1 10.34 1.66 Male No Sun Dinner 3
2 21.01 3.50 Male No Sun Dinner 3
3 23.68 3.31 Male No Sun Dinner 2
4 24.59 3.61 Female No Sun Dinner 4
total_bill tip size
count 244.000000 244.000000 244.000000
mean 19.785943 2.998279 2.569672
std 8.902412 1.383638 0.951100
min 3.070000 1.000000 1.000000
25% 13.347500 2.000000 2.000000
50% 17.795000 2.900000 2.000000
75% 24.127500 3.562500 3.000000
max 50.810000 10.000000 6.000000
/HOME1/users/personal/dana/miniconda3/envs/finance/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
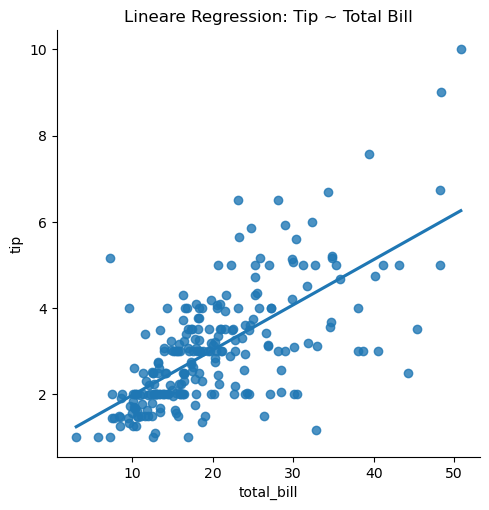
Das Einzeichnen der Regressionsgeraden in solch einen Scatterplot ist denkbar einfach, wir wollen uns aber jetzt näher mit der Bestimmung dieser Geraden beschäftigen.
Das Ziel der Regressionsanalyse ist es die Funktion \(f\) bzw. deren beschreibenden Parameter zu schätzen durch \(\hat f\). Für die einfache lineare Regression müssen daher nur noch die unbekannten Koeffizienten \(a\) und \(b\) der Gerade \( f(x)=a+bx\) aus den Beobachtungen \((x_1,y_1), \ldots, (x_n,y_n)\) geschätzt werden. Diese Schätzwerte bezeichnen wir mit \(\hat a\) und \(\hat b\) und werden mittels der Methode der kleinsten Quadrate bestimmt, d.h. unter allen Werten \(a \in \mathbb R\) und \(b \in \mathbb R\) wählen wir diejenigen Werte \(\hat a\) und \(\hat b\), für die die quadrierten Fehler zwischen Beobachtungen \(y_i\) und Modellvorhersagen \(\hat{y}_i =\hat f(x_i) = \hat a + \hat b x_i\) insgesamt am kleinsten sind, d.h. es wird das Minimierungsproblem
gelöst. Das folgende Beispiel illustriert die Methode der kleinsten Quadrate für einen kleinen Datensatz, indem die optimal ermittelte Gerade gegen eine beliebige andere Gerade für einen kleinen Datensatz betrachtet werden.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Datensatz zur Illustration
dataset = pd.DataFrame({
"x": [1, 2, 3, 4, 5],
"y": [17, 7, 11, 2, 3]
})
# Designmatrix X mit Intercept
X = np.column_stack([
np.ones(len(dataset)),
dataset["x"].to_numpy()
])
y = dataset["y"].to_numpy()
# Kleinste-Quadrate-Schätzer
beta, residuals, rank, s = np.linalg.lstsq(X, y, rcond=None)
beta0, beta1 = beta
# Vorhersagegitter
x_grid = np.linspace(dataset["x"].min(), dataset["x"].max(), 100)
X_grid = np.column_stack([np.ones(len(x_grid)), x_grid])
y_hat = X_grid @ beta
# Vergleichsgerade
def linear(x, a, b):
return a + b * x
y2_grid = linear(x_grid, a=4, b=1)
# Regressionswerte (für Residuenlinien)
dataset["fit"] = X @ beta
dataset["fit2"] = linear(dataset["x"], a=4, b=1)
dataset["residuals"] = dataset["y"] - dataset["fit"]
dataset["res2"] = dataset["y"] - dataset["fit2"]
# ==========
# PLOTS
# ==========
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
# (1) Daten, Regressionsgeraden & Residuen
ax = axes[0]
ax.scatter(dataset["x"], dataset["y"], label="Datenpunkte", color="black", zorder=4)
# OLS-Gerade
ax.plot(x_grid, y_hat, label="KQ-Regressionsgerade", color="blue")
# Vergleichsgerade
ax.plot(x_grid, y2_grid, label="Vergleichsgerade: y = 4 + x", linestyle="--", color="orange")
# Residuenlinien für OLS-Geraden (blau)
for xi, yi, fi in zip(dataset["x"], dataset["y"], dataset["fit"]):
ax.plot([xi, xi], [yi, fi], color="blue", linewidth=1)
# Residuenlinien für Vergleichsgerade (orange)
for xi, yi, fi2 in zip(dataset["x"], dataset["y"], dataset["fit2"]):
ax.plot([xi, xi], [yi, fi2], color="orange", linewidth=1)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Regression, Vergleichsgerade und Residuen")
ax.legend()
# (2) Residuenplot
ax2 = axes[1]
ax2.axhline(0, color="black", linewidth=1)
ax2.scatter(dataset["x"], dataset["residuals"], label="Residuen Regressions-Modell", color="blue")
ax2.scatter(dataset["x"], dataset["res2"], label="Residuen y=4+x", color="orange", marker="x")
ax2.set_xlabel("x")
ax2.set_ylabel("Residuen")
ax2.set_title("Residuenvergleich")
ax2.legend()
plt.tight_layout()
plt.show()
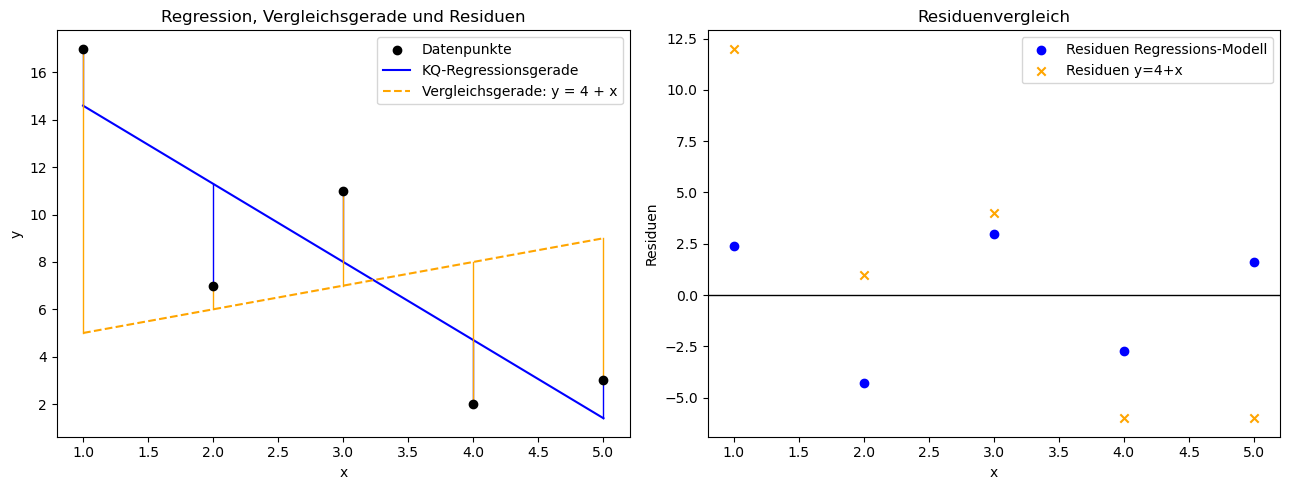
Die Berechnung der Schätzer \(\hat a\) und \(\hat b\) diskutieren wir gleich im Detail, aber ein Vergleich der Residuen sowie daraus resultierend der quadrierten Residuensummen zeigt deutlich, dass die blaue Regressionsgerade deutlich besser die Daten vorhersagt als die willkürlich gewählte orange Referenzgerade. Die folgenden Tabellen vergleichen die Residuen beider Modelle
x |
y |
ŷ=17.9−3.3x |
Ê=y-ŷ |
Ê^2 |
|---|---|---|---|---|
1 |
17 |
14.6 |
2.4 |
5.76 |
2 |
7 |
11.3 |
-4.3 |
18.49 |
3 |
11 |
8.0 |
3.0 |
9.00 |
4 |
2 |
4.7 |
-2.7 |
7.29 |
5 |
3 |
1.4 |
1.6 |
2.56 |
Summe der quadrierten Residuen: \(Q(17.9, -3.3) = 43.10\)
x |
y |
ŷ=4+x |
Ê=y-ŷ |
Ê^2 |
|---|---|---|---|---|
1 |
17 |
5 |
12 |
144 |
2 |
7 |
6 |
1 |
1 |
3 |
11 |
7 |
4 |
16 |
4 |
2 |
8 |
-6 |
36 |
5 |
3 |
9 |
-6 |
36 |
Summe der quadrierten Residuen: \(Q(4, 1) = 233\)
Die Minimierung der quadrierten Residuensumme sichert, dass jede beliebige andere Gerade eine größere quadrierte Residuensumme liefert. Zur Bestimmung der Kleinste-Quadrate Schätzer setzen wir den Gradienten Null
und lösen das erhaltene lineare Gleichungssystem für die Regressionskoeffizienten \(a\) und \(b\)
und erhalten somit die empirische Regressionsgerade
wobei
die empirische Kovarianz bzw. Varianz der Stichprobendaten beschreiben.
Für obiges Tips-Beispiel können wir also die Regressionskoeffizienten einfach aus den statistischen Kennzahlen berechnen.
### Berechnung mittels einfacher Formeln für lineare Regressionsgerade
y = tips.tip
x = tips["total_bill"]
b = x.cov(y) / x.var()
a = y.mean() - b * x.mean()
print("Regressionsgerade: y = a + b x mit Intercept a = %f und slope b = %f (Bestimmtheitsmaß R^2=%f)" %(a,b,x.corr(y)**2))
Regressionsgerade: y = a + b x mit Intercept a = 0.920270 und slope b = 0.105025 (Bestimmtheitsmaß R^2=0.456617)
Natürlich können wir auch direkt mit der Least-Squares Funktion von NumPy Doku für numpy.linalg.lstsq() die kleinste Quadrate Lösung berechnen. Die Erstellung der sogenannten \(n \times 2\) Designmatrix \(X\), welche in der ersten Spalte nur aus Einsen und in der zweiten Spalte alle x-Werte (hier Rechnungsdaten) enthält, werden in Abschnitt Lineares Modell für die einfache Regressionsgerade noch genauer besprochen.
#Kleinste-Quadrate via NumPy, siehe
# https://numpy.org/doc/stable/reference/generated/numpy.linalg.lstsq.html
X = np.column_stack((np.ones_like(x), x))
beta, residuals, rank, s = np.linalg.lstsq(X, y, rcond=None)
print("Koeffizienten via least squares: %s, Sum of squared residuals %s" % (beta,residuals[0]))
Koeffizienten via least squares: [0.92026961 0.10502452], Sum of squared residuals 252.78874385077606
8.2. Bestimmtheitsmaß#
Zur Modellgüte, also wie gut kann das verwendete Modell die Daten tatsächlich erklären, wird häufig das Bestimmtheitsmaß herangezogen, dessen Grundidee wir hier kurz erläutern möchten.
Die Werte \((y_1, \ldots, y_n)\) schwanken um das arithmetische Mittel \(\overline{y}\) und die Frage nach dem Anteil, welcher sich durch das Regressionsmodell mit den Vorhersagewerten \((\hat y_1, \ldots, \hat y_n)\) erklären lässt, führt auf das Bestimmtheitsmaß. Anstatt der empirischen Varianz \(s_y^2\) aller \(y\)-Werte \((y_1, \ldots, y_n)\) betrachten wir die damit sehr eng verbundene Total-Variation (TV) bzw. der Summe der quadratischen Abweichungen (SS)
Mit der Aufteilung \(y_i - \overline y = {\color{red}y_i - \hat y_i } + {\color{green}\hat y_i - \overline y }\) können wir die Total-Variation aber wegen
in den grünen Anteil \(\operatorname{TV}_{\mathrm{\small Modell}} = \operatorname{SS}_{\mathrm{\small Modell}}\) (\(\triangleq\) Modell-Variation), der die quadratischen Abweichungen von den Modellprognosen \(\hat y_i\) zum Mittel \(\overline y\) entspricht und den roten Anteil \(\operatorname{TV}_{\mathrm{\small Residuen}} = \operatorname{SS}_{\mathrm{\small Residuen}} = Q(\hat a, \hat b) = \sum\limits_{i=1}^n \left( y_i - \hat y_i \right)^2 = \sum\limits_{i=1}^n \hat{E}_i^2\) (\(\triangleq\) Residuen-Variation), der die quadrierten Residuen zusammenfasst, splitten denn der Zwischenterm \(Z\) verschwindet wegen \(\hat y_i = \overline y + \frac{s_{xy}}{s_x^2} (x_i - \overline x)\) sowie
Auch für beliebige lineare Regressionsmodelle gilt die Zerlegung \(\operatorname{TV}_{\mathrm{\small Total}} = {\color{red}\operatorname{TV}_{\mathrm{\small Residuen}}} + {\color{green}\operatorname{TV}_{\mathrm{\small Modell}}} = {\color{red}\operatorname{SS}_{\mathrm{\small Residuen}}} + {\color{green}\operatorname{SS}_{\mathrm{\small Modell}}}=\operatorname{SS}_{\mathrm{\small Total}}\), sofern die Koeffizienten mittels der Methode der kleinsten Quadrate ermittelt werden.
Bestimmtheitsmaß (für beliebige Regression) Das Bestimmtheitsmaß entspricht dem Verhältnis zwischen Modell-Variation und Total-Variation
und gibt damit den Anteil der Gesamtschwankung an, der sich auf das Regressions-Modell zurückführen lässt.
In obigen Tips-Beispiel lautet \(R^2=0.456617\), d.h. ca. 46 Prozent der Variation der Trinkgeldwerte werden durch das einfache Modell \(\hat y = \hat a + \hat b x\), d.h. den linearen Zusammenhang zur Gesamtrechnung erklärt, und die restlichen 54 Prozent gehen auf die Residuen-Variation zurück. Diese Schwankungen kann also das Modell nicht erklären und haben entweder andere Ursachen, die das Modell nicht erkennt oder die Residuen-Varianz ist allgemein eher groß.
Wegen der Zerlegung der Total-Variation in Modell- und Residuen-Variation folgt dann natürlich sofort
so dass für das Bestimmtheitsmaß immer \(0 \le R^2 \le 1\) gilt. Für die lineare Regressionsgerade entsprechen die beiden extremenen Grenzfälle gerade
\(R^2=1\), d.h. alle \((x_i,y_i)\) liegen auf Geraden wegen \(\operatorname{SS}_{\mathrm{\small Residuen}} = \sum\limits_{i=1}^n (y_i - \hat y_i)^2=0\), was nur für \(y_i = \hat y_i\) für alle \(i=1,\ldots,n\) gelten kann
\(R^2=0\), d.h. Regressionsgleichung erklärt nichts von der Total-Variation wegen \(\operatorname{SS}_{\mathrm{\small Modell}} = \sum\limits_{i=1}^n (\hat y_i-\bar{y})^2 = 0 \Leftrightarrow \operatorname{SS}_{\mathrm{\small Total}} = \sum\limits_{i=1}^n (y_i-\bar{y})^2 = \sum\limits_{i=1}^n (y_i - \hat y_i)^2 = \operatorname{SS}_{\mathrm{\small Residuen}}\)
Außerdem gilt für das Bestimmtheitsmaß der einfachen linearen Regression, bei der ein linearer Zusammenhang zwischen der zu erklärenden Variablen \(Y\) und der univariaten uabhängigen erklärenden Variablen \(X\) untersucht wird, immer \(R^2 = r_{xy}^2\), d.h. das Bestimmtheitsmaß entspricht dem quadrierten Korrelationskoeffizienten
denn aus \(\hat y_i = \overline y + \frac{s_{xy}}{s_x^2}(x_i- \overline x)\) folgt wieder \(\hat y_i -\overline y = \frac{s_{xy}}{s_x^2}(x_i- \overline x)\) und somit
Zusammenfassend sehen wir, dass die Berechnung der Regressionskoeffizienten über die Methode der kleinsten Quadrate auf einfach zu implementierende Formeln, die von empirschen Stichprobengrößen der beobachteten Daten abhängen. Insbesondere hängt der Anstieg der Regressionsgeraden \(\hat b\) von der empirischen Kovarianz bzw. Korrelation ab. Sind die empirische Kovarianz bzw. Korrelation positiv, so ist auch der Regressionskoeffizient \(\hat b =\frac{s_{xy}}{s_x^2}=\frac{s_{xy}}{s_x s_y} \cdot \frac{s_y}{s_x} = r_{xy}\cdot \frac{s_y}{s_x}\) ebenfalls positiv und folglich führt eine Erhöhung von \(x\) auch zu einer Erhöhung des Regressionswertes \(\hat y = \hat a + \hat b x\). Genauer erhalten wir für \(x_\text{neu} = x + \triangle x\) die Prognose \(\hat y_\text{neu} = \hat a + \hat b x_\text{neu} = \hat a + \hat b (x + \triangle x) = \hat a + \hat b x + \hat b \triangle x = \hat y + \hat b \triangle x\) und folglich \(\triangle \hat y = \hat y_\text{neu} - \hat y = \hat b \triangle x\), d.h. eine Erhöhung von \(x\) um eine Einheit (\(\triangle x=1\)) führt zur Veränderung um \(\hat b\) Einheiten für das Regressionsmodell.
Für die Regressionsgerade entspricht das Bestimmtheitsmaß, dass die Modellgüte zur Erklärung der abhängigen Variablen \(Y\) mittels der unabhängigen Variablen \(X\) für Daten \((x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n)\) angibt, gerade dem quadrierten Korrelationskoeffizienten und dies zeigt einfach nochmals eine alternative Sichtweise auf die Erfassung des Zusammenhangs zwischen \(X\) und \(Y\), denn der Fall \(r_{xy} = \pm 1 \Leftrightarrow R^2 = 1\) ist äquivalent zu einem perfekt linearen Zusammenhang zwischen \(Y\) und \(X\), welcher mit der linearen Regressionsgeraden dann natürlich perfekt wiedergegeben wird.
In den folgenden Abschnitten werden wir die Modelle zur Erklärung der unabhängigen Variablen \(Y\) erweitern und aufzeigen, dass die Berechnung für alle linearen Modelle einfach durch Matrix-Vektor Operationen verallgemeinert werden kann. Zudem werden wir viel einfacher diskutieren können, wann das Modell zu einer eindeutigen Lösung führt und in welchen Konstellationen dies nicht möglich ist. Außerdem liefert diese Verallgemeinerung einen umfassenden Überblick über Methoden der induktiven Statistik, so dass für die Regressionskoeffizienten unter gewissen Voraussetzungen Konfidenzintervalle oder statistische Tests abgeleitet werden können.
8.3. Lineare Modelle#
Bisher wurde in Abschnitt Motivation: Bestimmung der Regressionsgeraden der linearen Regression nur eine Regressionsgerade bestimmt, in dessem zugehörigen Modell die abhängige Variable \(Y\) (Regressand) durch eine unabhängige Variable \(X\) (Regressor) mittels einer linearen Funktion erklärt wird. Das Konzept der linearen Regression lässt sich allerdings deutlich erweitern, ohne dass die dahinterliegende Mathematik komplizierter wird, so dass beispielsweise auch eine quadratische Funktion den Einfluss von \(X\) auf \(Y\) erklären kann oder dass mehrere Regressoren \(X_1,X_2, \ldots,X_m\) Berücksichtigung finden. Wesentlich für diese Modelle ist nur, dass die Regressionskoeffizienten linear sind. Alle diese Regressionsmodelle sind unter dem Begriff lineare Modelle zusammengefassst.
Mathematisch lassen sich alle linearen Modelle, wie beipsielswesie die multivariate lineare Regression oder ANOVA, als \(Y = X \beta + E\) schreiben, wobei
\(X \triangleq \) Datenmatrix / Designmatrix des Regressors (erklärende / unabhängige Variablen)
\(Y \triangleq\) Datenvektor des Regressanden (abhängige zu erklärende Variable)
\(\beta \triangleq\) Koeffizientenvektor
\(E \triangleq\) Residuenvektor
mit dessen Lösung \(\hat \beta\), die wir im folgenden Abschnitt Kleinste Quadrate Lösung des linearen Modells kurz herleiten werden
man die Prognose \(\hat Y\) für die abhängige Variable \(Y\) für gegebene Daten \(X\) des Regressors bekommt.
8.3.1. Lineares Modell für die einfache Regressionsgerade#
Zur Bestimmung der Regressionsgeraden, die wir in Abschnitt Motivation: Bestimmung der Regressionsgeraden ausführlich diskutiert haben, erhalten wir das lineare Modell wie folgt
Koeffizientenvektor: \(\beta = \begin{pmatrix} a\\ b \end{pmatrix}\)
Designmatrix: \(X = \begin{pmatrix} 1 & x_1\\ 1 & x_2\\ \vdots & \vdots\\ 1 & x_n\\ \end{pmatrix}\)
Datenvektor: \(Y = \begin{pmatrix} Y_1\\ Y_2\\ \vdots\\ Y_n \end{pmatrix}\)
Residuenvektor: \(E = \begin{pmatrix} E_1\\ E_2\\ \vdots\\ E_n \end{pmatrix}\)
denn \(Y = X \beta + E\) entspricht gerade elementweise \(Y_i = a + b x_i + E_i\) für alle \(i=1, \ldots, n\).
Anmerkung: Üblicherweise modelliert man für die linearen Modelle den Residuenvektor als \(n-\)dimensionalen Zufallsvektor mit \(\mathbb{E} E = 0\) und setzt die Beobachtungen der \(X\) Variablen, die in die Designmatrix \(X\) eingehen als gegeben (determinstisch) an, so dass dann die Verteilung des Zufallvektors \(Y = X \beta + E\) von der Verteilung von des Residuenvektors \(E\) abhängt. Soll auch \(X\) als Zufallsvariable modelliert werden, entspricht die Modell-Prognose dem bedingten Erwartungswert \(\hat Y = \mathbb{E}(Y | X)\).
8.3.2. Lineares Modell für die Anpassung einer polynomiellen Funktion#
Für die Bestimmung der quadratischen Regressionsfunktion: \(Y_i = a + bx_i + cx_i^2 + E_i\) stellen wir entsprechend einfaches folgendes lineares Modell auf:
Koeffizientenvektor: \(\beta = \begin{pmatrix} a\\ b\\ c \end{pmatrix}\)
Designmatrix: \(X = \begin{pmatrix} 1 & x_1 & x_1^2\\ 1 & x_2 & x_2^2\\ \vdots & \vdots & \vdots\\ 1 & x_n & x_n^2\\ \end{pmatrix}\)
Das Aufstellen eines Modells hat also lediglich auf Designmatrix \(X\) und Koeffizientenvektor \(\beta\) Einfluss, so dass die Modelle sehr einfach angepasst werden können. Das Anpassen einer polynomiellen Funktion für das Modell \(Y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \ldots + \beta_m x_i^m + E_i\) wird einfach durch die modifizierte Designmatrix \(X = \begin{pmatrix} 1 & x_1 & x_1^2 & \ldots & x_1^m\\ 1 & x_2 & x_2^2 & \ldots & x_2^m\\ \vdots & \vdots & \ldots & \vdots\\ 1 & x_n & x_n^2 & \ldots & x_n^m\\ \end{pmatrix}\) und Koeffizientenvektor \(\beta = \begin{pmatrix} \beta_0\\ \beta_1\\ \vdots \\ \beta_m \end{pmatrix}\) beschrieben.
8.3.3. Lineare Regression mit \(m\) Prediktoren / Regressoren#
Ebenso können wir jetzt mehrere Prediktoren zur Modellierung \(Y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots \beta_m x_{mi} + E_i\) aufnehmen, so dass
Koeffizientenvektor: \(\beta = \begin{pmatrix} \beta_0\\ \beta_1\\ \vdots \\ \beta_m \end{pmatrix}\) und
Designmatrix: \(X = \begin{pmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1m}\\ 1 & x_{21} & x_{22} & \cdots & x_{2m}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nm}\\ \end{pmatrix}\)
zu wählen sind.
8.4. Kleinste Quadrate Lösung des linearen Modells#
Wir betrachten das lineare Modell
wobei \(X\in\mathbb R^{n\times p}\), (\(p = m+1\)) die Designmatrix, \(Y\in\mathbb R^{n}\) der Datenvektor, \(\beta\in\mathbb R^{p}\) der unbekannte Koeffizientenvektor und \(E \in \mathbb R^n\) der Residuenvektor ist. Üblicherweise ist Anzahl der Daten \(n>p\). Gesucht ist die Kleinste-Quadrate-(KQ/OLS)-Schätzung
8.4.1. Ableitung der Normalengleichungen#
Durch Ausmultiplizieren und Ableiten erhalten wir
Der Gradientenvektor \(\nabla\), d.h. der Vektor der partiellen Ableitungen der Residuenquadratsumme \(\frac{ \partial Q(\beta)}{\partial \beta_k}\), \(k=0,1,\ldots,m\) lautet
Setzt man \(\nabla_\beta Q(\beta)=0\), entstehen die Normalengleichungen
Falls die Designmatrix \(X\) vollen Spaltenrang hat (\(\mathrm{rang}(X)=p\)), ist \(X^{\top}X\) invertierbar und es gilt die geschlossene Form
Diese Matrixform verallgemeinert die in Abschnitt Motivation: Bestimmung der Regressionsgeraden hergeleiteten Formeln der einfachen Regression und zeigt gleichzeitig auf, wie wir lineare Regressionsmodelle mittels NumPy einfach selbstständig berechnen können. Mittels der letzten Gleichung folgt für zentrierte Residuen \(E\) mit \(\mathbb{E}E=0\) und \(\Sigma = \operatorname{cov}(E) = \mathbb{E} \left( E^\top E \right)\)
Mit der kleinste Quadrate Lösung erhalten wir außerdem
wobei \(P_L\) den Projektionsoperator auf den linearen Unterraum \(L = \operatorname{range}(X)=\left\lbrace y \in \mathbb{R}^n: \, y = X \beta, \beta \in \mathbb{R}^p \right\rbrace \), der durch die Spalten der Designmatrix \(X\) aufgespannt wird, und \(P_{L^\perp} = I - P_L\) den Projektionsoperator auf den orthogonalen Unterraum \(L^\perp = \left\lbrace v \in \mathbb{R}^n: v^\top X \beta = 0, \, \beta \in \mathbb{R}^p \right\rbrace\).
Folglich erhalten wir
Unter den Standardannahmen der linearen Modell, dass die Residuen aller beobachteten Daten identisch und unabhängig verteilt sind und einer Normalverteilung folgen, reduziert sich die Kovarianzmatrix auf eine Diagonalmatrix mit
erhält man also einfach für die Kovarianzmatrizen
und wegen der Normalverteilungsannahme der Residuen
\(E \sim \mathcal{N}_p \left( 0, \Sigma \right)=\mathcal{N}_p \left( 0, \sigma^2 I \right) \Leftrightarrow E_i \sim \mathcal{N}(0,\sigma^2)\) (iid) folglich für die geschätzten Koeffizienten ebenfalls die multivariate Normalverteilung
welche Grundlage für zahlreiche statistische Tests, die wir in Abschnitt Statistische Tests im linearen Modell näher betrachten, bildet.
8.5. Umsetzung mit NumPy#
Für obigen Trinkgeld-Datensatz…
#Erzeugen Designmatrix
nx = len(x)
ny = len(y)
if nx==ny:
n = nx
else:
print("Achtung: x und y passen nicht zusammen!")
X = np.column_stack((np.ones_like(x), x))
print(X[:5])
#Datenvektor
Y = y
print(Y[:5])
[[ 1. 16.99]
[ 1. 10.34]
[ 1. 21.01]
[ 1. 23.68]
[ 1. 24.59]]
0 1.01
1 1.66
2 3.50
3 3.31
4 3.61
Name: tip, dtype: float64
Lösung des Least-Squares Problems
#least squares
beta, res, rank, s = np.linalg.lstsq(X,Y, rcond= None)
print(beta)
print("sum of squared res: %s, rank(X^T X): %s" % (res[0],rank))
[0.92026961 0.10502452]
sum of squared res: 252.78874385077606, rank(X^T X): 2
#Normalengleichung als lineares Gleichungssystem loesen
A = X.transpose() @ X
b = X.transpose() @ Y
beta2 = np.linalg.solve(A, b)
#print(A)
#print(b)
print(beta2)
[0.92026961 0.10502452]
#mittels inverser beta direkt berechnen
A_inv = np.linalg.inv(A)
beta3 = A_inv @ b
print(beta3)
[0.92026961 0.10502452]
8.6. Umsetzung mit Statistik-Paketen#
Es gibt zahlreiche Pakete, mit deren Hilfe Regressionsmodelle berechnet werden können. Wir betrachten die folgenden Pakete
Statsmodels
Klassisches Statistik-Framework (ähnlich wie in R): liefert Regressionskoeffizienten, Standardfehler, p-Werte, Konfidenzintervalle, ANOVA, Diagnoseplots und robuste Standardfehler.
Ideal für: wissenschaftliche Statistik, Ökonometrie, Finance, detaillierte Modellanalysesklearn
Machine-Learning-Bibliothek mit Fokus auf Vorhersagemodellen. Schnelle, robuste Implementierung von linearer Regression, aber ohne statistische Tests oder p-Werte.
Ideal für: Vorhersage, ML-Pipelines, skalierbare Modellescipy
Sehr einfache Möglichkeit für eine klassische lineare Regression (y~x). Gibt Steigung, Intercept, r-Wert, p-Wert und Standardfehler zurück – kompakt und leicht zu verwenden.
Ideal für: schnelle Analysen, einfache lineare Zusammenhängelinearmodels (Installation via pip!)
Erweiterte Ökonometrie-Bibliothek: OLS, IV/2SLS, GMM, Fama-MacBeth, Paneldaten (Fixed/Random Effects) und cluster-robuste Fehler.
Ideal für: Finance, Ökonometrie, Paneldatenmodelle, Faktorrecherche (CAPM, Fama-French).
#mittels Paket satsmodels
#https://www.statsmodels.org/dev/generated/statsmodels.regression.linear_model.OLS.html
import statsmodels.api as sm
#Erstellen der Designmatrix
X1 = sm.add_constant(x)
print(X1)
# Modell schaetzen (Kleinste Quadrate = ordinary least squares)
model1 = sm.OLS(Y, X1).fit()
# Ergebnisse anzeigen
print(model1)
print(model1.summary())
const total_bill
0 1.0 16.99
1 1.0 10.34
2 1.0 21.01
3 1.0 23.68
4 1.0 24.59
.. ... ...
239 1.0 29.03
240 1.0 27.18
241 1.0 22.67
242 1.0 17.82
243 1.0 18.78
[244 rows x 2 columns]
<statsmodels.regression.linear_model.RegressionResultsWrapper object at 0x78af56119b90>
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.457
Model: OLS Adj. R-squared: 0.454
Method: Least Squares F-statistic: 203.4
Date: Fri, 16 Jan 2026 Prob (F-statistic): 6.69e-34
Time: 12:07:20 Log-Likelihood: -350.54
No. Observations: 244 AIC: 705.1
Df Residuals: 242 BIC: 712.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.9203 0.160 5.761 0.000 0.606 1.235
total_bill 0.1050 0.007 14.260 0.000 0.091 0.120
==============================================================================
Omnibus: 20.185 Durbin-Watson: 2.151
Prob(Omnibus): 0.000 Jarque-Bera (JB): 37.750
Skew: 0.443 Prob(JB): 6.35e-09
Kurtosis: 4.711 Cond. No. 53.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Alternativ kann die Designmatrix auch erstellt werden, indem das Modell mittels Formeln beschrieben wird:
from statsmodels.formula.api import ols
model1_v2 = ols("tip~total_bill", data = tips).fit()
print(model1_v2.summary())
#print(sm.stats.anova_lm(model1_v2))
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.457
Model: OLS Adj. R-squared: 0.454
Method: Least Squares F-statistic: 203.4
Date: Fri, 16 Jan 2026 Prob (F-statistic): 6.69e-34
Time: 12:07:20 Log-Likelihood: -350.54
No. Observations: 244 AIC: 705.1
Df Residuals: 242 BIC: 712.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.9203 0.160 5.761 0.000 0.606 1.235
total_bill 0.1050 0.007 14.260 0.000 0.091 0.120
==============================================================================
Omnibus: 20.185 Durbin-Watson: 2.151
Prob(Omnibus): 0.000 Jarque-Bera (JB): 37.750
Skew: 0.443 Prob(JB): 6.35e-09
Kurtosis: 4.711 Cond. No. 53.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
X_design = model1_v2.model.exog
#names = model1_v2.model.exog_names
N, p = X_design.shape
print("Dimensionen des linearen Modells: N=%s (sample size), p = %s (model parameters)" % (N,p))
#Designmatrix
print(X_design[:10])
Dimensionen des linearen Modells: N=244 (sample size), p = 2 (model parameters)
[[ 1. 16.99]
[ 1. 10.34]
[ 1. 21.01]
[ 1. 23.68]
[ 1. 24.59]
[ 1. 25.29]
[ 1. 8.77]
[ 1. 26.88]
[ 1. 15.04]
[ 1. 14.78]]
#mittels sklearn
from sklearn.linear_model import LinearRegression
X2 = x.to_numpy().reshape(-1, 1)
model2 = LinearRegression().fit(X2, Y)
print("Intercept:", model2.intercept_)
print("Slope:", model2.coef_[0])
print("R²:", model2.score(X2, Y))
Intercept: 0.9202696135546731
Slope: 0.10502451738435337
R²: 0.45661658635167657
from scipy.stats import linregress
model3 = linregress(x, y)
print(model3)
LinregressResult(slope=0.1050245173843534, intercept=0.9202696135546726, rvalue=0.6757341092113641, pvalue=6.692470646864404e-34, stderr=0.007364789848762602, intercept_stderr=0.1597347463764325)
from linearmodels.iv import IV2SLS
df = pd.DataFrame({"y": y, "x": x})
model4 = IV2SLS.from_formula("y ~ 1 + x", data=df)
results4 = model4.fit()
print(results4.summary)
OLS Estimation Summary
==============================================================================
Dep. Variable: y R-squared: 0.4566
Estimator: OLS Adj. R-squared: 0.4544
No. Observations: 244 F-statistic: 80.349
Date: Fri, Jan 16 2026 P-value (F-stat) 0.0000
Time: 12:07:28 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.9203 0.2046 4.4985 0.0000 0.5193 1.3212
x 0.1050 0.0117 8.9638 0.0000 0.0821 0.1280
==============================================================================
#via orig. DataFrame
model5 = IV2SLS.from_formula("tip ~ 1 + total_bill", data=tips)
results5 = model5.fit()
print(results5.summary)
OLS Estimation Summary
==============================================================================
Dep. Variable: tip R-squared: 0.4566
Estimator: OLS Adj. R-squared: 0.4544
No. Observations: 244 F-statistic: 80.349
Date: Fri, Jan 16 2026 P-value (F-stat) 0.0000
Time: 12:07:28 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 0.9203 0.2046 4.4985 0.0000 0.5193 1.3212
total_bill 0.1050 0.0117 8.9638 0.0000 0.0821 0.1280
==============================================================================
8.7. Statistische Tests im linearen Modell#
Alle obigen Ausgaben enthalten zusätzliche Informationen zu statistischen Tests, die für das gesamte Modell, die einzelnen Koeffizienten sowie die Residuen durchgeführt werden. Diese Tests basieren auf der Normalverteilungsannahme der unabhängigen und varianzhomogenen Residuen, wie wir am Ende von Abschnitt Kleinste Quadrate Lösung des linearen Modells diskutiert haben.
Wir betrachten hier das 1. Modell, welches mittels ‘statsmodels’ durch Formeln beschrieben wurde etwas genauer
print(model1_v2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.457
Model: OLS Adj. R-squared: 0.454
Method: Least Squares F-statistic: 203.4
Date: Fri, 16 Jan 2026 Prob (F-statistic): 6.69e-34
Time: 12:07:28 Log-Likelihood: -350.54
No. Observations: 244 AIC: 705.1
Df Residuals: 242 BIC: 712.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.9203 0.160 5.761 0.000 0.606 1.235
total_bill 0.1050 0.007 14.260 0.000 0.091 0.120
==============================================================================
Omnibus: 20.185 Durbin-Watson: 2.151
Prob(Omnibus): 0.000 Jarque-Bera (JB): 37.750
Skew: 0.443 Prob(JB): 6.35e-09
Kurtosis: 4.711 Cond. No. 53.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Die Freiheitsgrade ergeben sich direkt aus dem Modell und können unmittelbar aus der \(n \times p\) Designmatrix mit \(n\) (Anzahl der beobachteten Daten) Zeilen und \(p\) (Anzahl der Modell-Parameter, d.h. Länge des Koeffizienten-Vektors \(\beta\)) abgeleitet werden.
print("Dimensionen des linearen Modells: n = %s (sample size), p = %s (model parameters in beta)" % (N,p))
print("Freiheitsgrade (df): df_resid = %s = n-p, df_model = %s = p-1" % (model1_v2.df_resid, model1_v2.df_model))
Dimensionen des linearen Modells: n = 244 (sample size), p = 2 (model parameters in beta)
Freiheitsgrade (df): df_resid = 242.0 = n-p, df_model = 1.0 = p-1
Die Anova-Tabelle des Modells zeigt die wichtigsten Quadratsummen bzw. davon abgeleitete Mean Squares (Quadratsumme skaliert mit Freiheitsgraden), mit deren Hilfe der Fisher-Test mit der Nullhypothese \(H_0: \beta_1 = \ldots = \beta_{p-1} = 0\) berechnet wird
print(sm.stats.anova_lm(model1_v2))
df sum_sq mean_sq F PR(>F)
total_bill 1.0 212.423733 212.423733 203.357723 6.692471e-34
Residual 242.0 252.788744 1.044582 NaN NaN
Da die Fisher-Statistik sehr groß ist, ist der entsprechende p-value \(P(F>203.358) = 6.692471e-34\) extrem klein, so dass die Nullhypothese verworfen wird und somit ein signifikanter Nachweis des Modells gegeben ist. Genauer lautet ja die Modell-Prognose \(\hat Y = X \hat \beta\), d.h. für gegebenes \(x\) (hier die Gesamtrechnung) wird für unser Modell, welches auf der einfachen Regressionsgerade basiert somit \(\hat y = \hat \beta_0 + \hat \beta_1 x = \hat a + \hat b\) vorhergesagt. Unter der Nullhpythese, die sich hier wegen \(p-1=1\) nur auf \(H_0: \beta_1 = b=0\) reduziert, würde dann allerdings nur noch die triviale Prognose \(\hat y = \hat \beta_0 = \hat a = \overline y\) ergeben. Da die Nullhypthese allerdings verworfen wird, haben wir somit den Nachweis, dass das Modell signifikant zur Erklärung der zu erklärednen Variablen \(Y\) beitragen kann.
Die Tabelle der Regressionskoeffizienten enthält jeweils einen t-Test für \(H_0: \beta_i = 0\), welcher auf der Normalverteilungsannahme der Residuen (sowie deren Unabhängigkeit und Varianzhomogenität), die wir ausführlich in Abschnitt Kleinste Quadrate Lösung des linearen Modells diskutiert haben, und daraus resultierend aus
Die letzte Tabelle der ausführlichen Auswertungstabelle enthält eine Zusammenfassung der Residuen-Auswertung, welche eine Überprüfung obiger Testvoraussetzungen wie der Normalverteilung, Unabhängigkeit und Varianzhomogenität zulassen.
8.8. Varianzanalyse (ANOVA) als lineares Modell#
Im vorherigen Abschnitt haben wir gesehen, dass bei der Auswertung linearer Modelle ANOVA-Tabellen erzeugt werden. ANOVA steht für Analysis of Variance und basiert auf der Zerlegung der Totalvariation, die wir für Regressionsmodelle bereits diskutiert haben.
Die einfaktorielle ANOVA untersucht den Einfluss einer kategoriellen Variablen mit \(m\) verschiedenen Ausprägungen auf die metrische Variable \(Y\). Alle bisher betrachteten linearen Regressions-Modelle hatten nur metrische Variablen als Regressoren bzw. erklärenden Variablen im Modell zur Vorhersage von \(Y\) modelliert. Wir wollen hier nur die Grundidee veranschaulichen und aufzeigen wie sich die ANOVA in das Konzept der linearen Modelle integriert.
Oben haben wir bereits den Einfluss der Gesamtrechnung auf das Trinkgeld mittels eines einfachen linearen Regressionsmodells untersucht und gesehen, dass das Bestimmtheitsmaß \(R^2\approx 0.46\) beträgt. Somit lassen sich ca. 46 Prozent der Variation der Trinkgeldwertes durch das Modell, welches einen linearen Zusammenhang zur Gesamtrechnung ansetzt, erklären und die verbleibenden 54 Prozent der Schwankung gehen auf die Residuen zurück. Andere Einflussfaktoren auf das gezahlte Trinkgeld, wie beispielsweise die Kundenzufriedenheit mit Service und Essensqualität werden von dem Modell nicht berücksichtigt und können natürlich die Schwankungen zusätzliche beeinflussen, so dass die Residuen automatisch größer werden. Ein statistisches Modell kann natürlich versuchen auch mehrere Einflussfaktoren gleichzeitig aufzunehmen, wenn die Daten dies zulassen. Der Tips-Datensatz enthält neben der Gesamtrechnung und den Trinkgeldern beispielsweise noch den Wochentag und die Information, ob die Gäste mittags oder abends im Restaurant waren.
print(tips.dtypes)
total_bill float64
tip float64
sex category
smoker category
day category
time category
size int64
dtype: object
Die folgende Graphik zeigt beispielsweise den Zusammenhang der metrischen Variablen in Abhängigkeit von der Zeit
sns.pairplot(tips, hue="time")
/HOME1/users/personal/dana/miniconda3/envs/finance/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
<seaborn.axisgrid.PairGrid at 0x78af4a628a90>
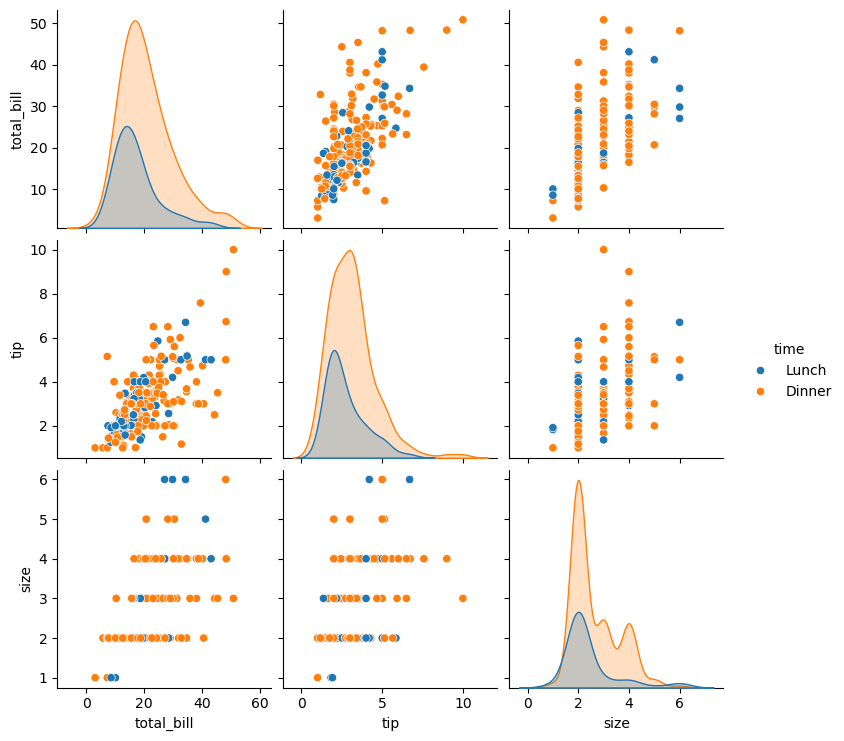
Zur Illustration wie die ANOVA funktioniert, wollen wir jeweils den Einfluss des Wochentags und der Tageszeit auf die gezahlten Trinkgelder betrachten.
Die folgenden Boxplots visualisieren den Zusammenhang zwischen Trinkgeld und Wochentag bzw. Trinkgeld und Tageszeit.
tips.boxplot(column="tip", by="day")
tips.boxplot(column="tip", by="time")
<Axes: title={'center': 'tip'}, xlabel='time'>
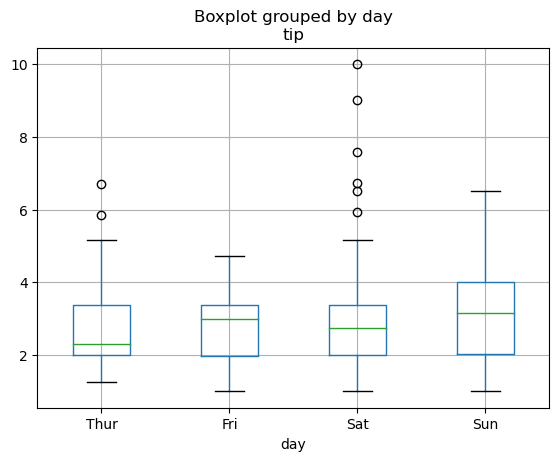
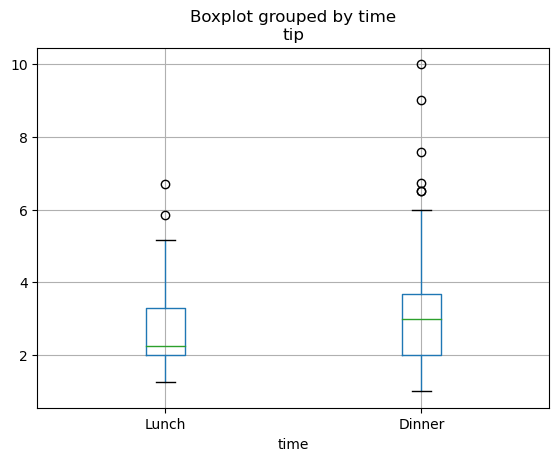
Die relevanten Zahlen zu der können wir natürlich auch einfach berechnen:
tips.groupby("day")["tip"].agg(
count="count",
mean="mean",
std="std",
var="var",
q25=lambda x: x.quantile(0.25),
median="median",
q75=lambda x: x.quantile(0.75),
)
/tmp/ipykernel_2432072/854309238.py:1: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
tips.groupby("day")["tip"].agg(
| count | mean | std | var | q25 | median | q75 | |
|---|---|---|---|---|---|---|---|
| day | |||||||
| Thur | 62 | 2.771452 | 1.240223 | 1.538154 | 2.0000 | 2.305 | 3.3625 |
| Fri | 19 | 2.734737 | 1.019577 | 1.039537 | 1.9600 | 3.000 | 3.3650 |
| Sat | 87 | 2.993103 | 1.631014 | 2.660208 | 2.0000 | 2.750 | 3.3700 |
| Sun | 76 | 3.255132 | 1.234880 | 1.524929 | 2.0375 | 3.150 | 4.0000 |
tips.groupby("time")["tip"].agg(
count="count",
mean="mean",
std="std",
var="var",
q25=lambda x: x.quantile(0.25),
median="median",
q75=lambda x: x.quantile(0.75),
)
/tmp/ipykernel_2432072/1115663294.py:1: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
tips.groupby("time")["tip"].agg(
| count | mean | std | var | q25 | median | q75 | |
|---|---|---|---|---|---|---|---|
| time | |||||||
| Lunch | 68 | 2.728088 | 1.205345 | 1.452857 | 2.0 | 2.25 | 3.2875 |
| Dinner | 176 | 3.102670 | 1.436243 | 2.062793 | 2.0 | 3.00 | 3.6875 |
Die Werte und die Boxplots zeigen, dass beide Faktoren einen leichten Einfluss auf die Trinkgelder haben könnten. Eine objektive Entscheidung, ob die Unterschiede nur zufällig oder wirklich systematisch sind, kann mittels ANOVA statistisch beantwortet werden.
Im ersten Beispiel sehen wir \(m=4\) und im zweiten Beispiel \(m=2\) Gruppen.
Allgemein können die Daten für die einfaktorielle Varianzanalyse mit insgesamt \(n=n_1+\ldots+n_m\) Daten aus den \(m\) Gruppen wie folgt übersichtlich gruppenweise dargestellt werden.
Stichprobe |
Index |
Gruppe 1 |
Gruppe 2 |
… |
Gruppe m |
|---|---|---|---|---|---|
1 |
\(Y_{11}\) |
\(Y_{21}\) |
… |
\(Y_{m1}\) |
|
2 |
\(Y_{12}\) |
\(Y_{22}\) |
… |
\(Y_{m2}\) |
|
⋮ |
⋮ |
⋮ |
⋱ |
⋮ |
|
\(n_k\) |
\(Y_{1n_1}\) |
\(Y_{2n_2}\) |
… |
\(Y_{mn_m}\) |
|
Gruppenmittel |
\(\overline{Y}_k\) |
\(\overline{Y}_1\) |
\(\overline{Y}_2\) |
… |
\(\overline{Y}_m\) |
Gesamtmittel |
\(\overline{Y} = \frac 1n \left( \right.\) |
\(n_1 \overline{Y}_1\) |
\(+n_2 \overline{Y}_2\) |
\(+ \ldots\) |
\( \left. + n_m \overline{Y}_m \right) \) |
Der Index \(k=1\) stellt die Stichprobenwerte der ersten Gruppe, hier also dem Wochentag Thur / Do dar, \(k=2\) alle TRinkgelder für Freitag usw. Allgemein beschreibt der Wert \(Y_{kj}\) also im ersten Beispiel das Trinkgeld des \(j\)-ten Gastes am \(k\)-ten Tag.
8.8.1. Varianzzerlegung der ANOVA#
Das statistische Modell der ANOVA für den \(j\)-ten Messwert der \(k\)-ten Gruppe als Zufallsvariable
mit unabhängigen und identisch verteilten überlagerten Fehlerterm \(E_{kj} \sim \mathcal{N}(0,\sigma^2)\) dar, so dass \(\mathbb{E}(Y_{kj}) = \mu_k\) und folglich die Prognose mit \(\hat Y_k = \hat \mu_k = \overline Y_k\) dem Gruppenmittel entspricht.
Die Varianzanalyse basiert auf der Zerlegung der Gesamtvariation der abhängigen Variablen, hier also den Trinkgeldern in einen Modell-Anteil, genauer die Variation, die auf den Faktor, welchen wir einfach mit \(A\) bezeichnen werden (Variation zwischen den Gruppen) und den Residuen-Anteil (Variation innerhalb der Gruppen), ähnlich wie wir es bei der Herleitung des Bestimmtheitsmaßes gesehen haben.
Unter der Nullhypothese \(H_0: \, \mu_1 = \mu_2 = \ldots = \mu_m\) und obiger Annahme unabhängiger und normalverteilter Fehlerterme \(E_{kj} \sim \mathcal{N}(0,\sigma^2)\) mit homogenen Varianzen (\(\sigma^2\) hängt also nicht von Gruppe \(k\) ab) besitzt die Testgröße
eine Fisher-Verteilung. Hat der Faktor \(A\) und somit das Modell einen großen Einfluß auf die erklärende Variable \(Y\), so werden die Gruppenmittelwerte sich stark unterscheiden, so dass die Quadratsummen des Faktors \(\operatorname{SS}_{A}\) groß sind. Hat hingegen der Faktor keinen wesentlichen Einfluss ist die Schwankung innerhalb der Gruppen deutlich größer. Große Testwerte sprechen also gegen die Nullhypothese. Ist der entsprechende p-Value kleiner als die vorgegebene Irrtumswahtscheinlichkeit \(\alpha\), die wir hier einfach mit 5% ansetzen, wird \(H_0\) verworfen und stattdessen die Alternativhypothese \(H_1\) angenommen. Diese besagt, dass es mindestens einen Mittelwert-Unterschied \(\mu_i \neq \mu_j\) gibt.
Ähnlich sieht es bei UNtersuchungen nach dem Einfluss des Wochentags aus.
#import statsmodels.api as sm
from statsmodels.formula.api import ols
model_day = ols("tip ~ C(day)", data=tips).fit()
anova_day = sm.stats.anova_lm(model_day, typ=1)
anova_day
| df | sum_sq | mean_sq | F | PR(>F) | |
|---|---|---|---|---|---|
| C(day) | 3.0 | 9.525873 | 3.175291 | 1.672355 | 0.173589 |
| Residual | 240.0 | 455.686604 | 1.898694 | NaN | NaN |
Bei 5%-tiger Irrtumswahrscheinlichkeit hat der Test, der den Einfluss des Wochentags auf das Trinkgeld untersucht, keine Einwände gegen die Nullhypothese \(H_0: \, \mu_1 = \mu_2 = \mu_3 = \mu_4\), da der p-Value die Irrtumswahrscheinlichkeit überschreitet. Somit kann die Alternativhypothese, dass sich die gezahlten Trinkgelder mindestens zwischen zwei verschiedenen Wochentagen unterscheiden (\(H_1: \, \exists \mu_i \neq \mu_j\)) nicht statistisch signifikant nachgewiesen werden. Der Wochentag hat also keinen Einfluss auf die durchschnittlich gezahlten Trinkgelder.
model_time = ols("tip ~ C(time)", data=tips).fit()
anova_time = sm.stats.anova_lm(model_time, typ=1)
print(anova_time)
#fuer bereits als kategorielle Daten initierte Variablen kann C() auch weggelassen werden
print(tips.dtypes)
model_time2 = ols("tip ~ time", data=tips).fit()
anova_time2 = sm.stats.anova_lm(model_time2, typ=1)
print(anova_time2)
df sum_sq mean_sq F PR(>F)
C(time) 1.0 6.882181 6.882181 3.633815 0.057802
Residual 242.0 458.330296 1.893927 NaN NaN
total_bill float64
tip float64
sex category
smoker category
day category
time category
size int64
dtype: object
df sum_sq mean_sq F PR(>F)
time 1.0 6.882181 6.882181 3.633815 0.057802
Residual 242.0 458.330296 1.893927 NaN NaN
Bei 5%-tiger Irrtumswahrscheinlichkeit hat der Test, der den Einfluss der Tageszeit auf das Trinkgeld untersucht, keine Einwände gegen die Nullhypothese \(H_0: \, \mu_1 = \mu_2\), da der p-Value die Irrtumswahrscheinlichkeit überschreitet. Somit kann die Alternativhypothese, dass sich die gezahlten Trinkgelder zwischen Lunch und Dinner unterscheiden (\(H_1: \, \mu_1 \neq \mu_2\)) nicht statistisch signifikant nachgewiesen werden.
Bei dem Vergleich der Mittelwerte von genau 2 Gruppen, führt man üblicherweise einen doppelten t-Test durch, der zumindest für zweiseitige Tests allerdings exakt mit der ANOVA übereinstimmt, da die Testgröße der ANOVA wegen \(F=T^2\) mit der quadrierten Testgröße des t-Tests übereinstimmt.
Hat man eine signifikante ANOVA durchgeführt, interessiert natürlich zwischen welchen Gruppen konkret der Mittelwertunterschied auftritt. Dies beantwort die klassische ANOVA-Auswertung allerdings nicht und klassischerweise führt man dann paarweise Mittelwertvergleiche durch. Für \(m\) Gruppen ergeben sich allerdings \(\binom{m}{2} = \frac{m(m-1)}{2}\) Vergleiche und somit automatisch zur Problematik des multiplen Testens.
Eine Interessante Alternative zu klassischen PostHoc-Mittelwertvergleichen liefert allerdings die Auswertung des zugehörigen linearen Modells, dass sich durch Einführung von Dummy-Variablen ergibt.
8.8.2. Dummy-Kodierung der Faktorvariablen#
Das statistische Modell der einfaktoriellen ANOVA beschreibt den \(j\)-ten Messwert der \(k\)-ten Gruppe kann durch Einführung von \(m\) Dummy-Variablen, deren Werte fast immer Null sind
auch als Regressionsmodell geschrieben werden. Da jeder Datenpunkt sich zu genau einer Gruppe zuordnen lässt, summieren sich die Dummyvariablen jeweils zu 1. Daher genügen wegen \(x_1 = 1 - x_2 - \ldots - x_m\) tatsächlich sogar \(m-1\) Dummyvariablen
Damit können wir die ANOVA als lineares Modell \(Y = X \cdot \beta + E\) mit dem Beobachtungsvektor
der künstlichen \(n \times m\) Designmatrix \(X\), also der Matrix der Dummyvariablen, dem unbekannten Vektor der Modellparameter
und dem ebenfalls unbekannten Fehlervektor
schreiben. Die Auswertung des linearen Modells gibt neben der klassischen Varianzzerlegung zusätzliche Mittelwertvergleiche, da mit Ausnahme des Intercepts \(\beta_0=\mu_1\) die restlichen Koeffizienten wegen \(\beta_1 = \alpha_2 - \alpha_1 = \mu_2 - \mu_1\), \(\beta_2 = \alpha_3 - \alpha_1 = \mu_3 - \mu_1\) usw. gerade den Vergleich der Gruppenmittelwerte bzw. Gruppeneffekte zur Referenzgruppe bechreiben und geschätzt werden. Die zugehörigen t-Tests untersuchen jeweils die Hypothesen \(H_0: \, \beta_k = 0\), was äquivalent zu \(H_0: \, \mu_k = \mu_1\) bzw. \(H_0: \, \alpha_k = \alpha_1\) ist.
#model_day = ols("tip ~ C(day)", data=tips).fit()
print(model_day.summary())
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.020
Model: OLS Adj. R-squared: 0.008
Method: Least Squares F-statistic: 1.672
Date: Fri, 16 Jan 2026 Prob (F-statistic): 0.174
Time: 12:07:31 Log-Likelihood: -422.43
No. Observations: 244 AIC: 852.9
Df Residuals: 240 BIC: 866.8
Df Model: 3
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept 2.7715 0.175 15.837 0.000 2.427 3.116
C(day)[T.Fri] -0.0367 0.361 -0.102 0.919 -0.748 0.675
C(day)[T.Sat] 0.2217 0.229 0.968 0.334 -0.229 0.673
C(day)[T.Sun] 0.4837 0.236 2.051 0.041 0.019 0.948
==============================================================================
Omnibus: 82.801 Durbin-Watson: 1.962
Prob(Omnibus): 0.000 Jarque-Bera (JB): 238.276
Skew: 1.492 Prob(JB): 1.82e-52
Kurtosis: 6.811 Cond. No. 5.28
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(model_time.summary())
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.015
Model: OLS Adj. R-squared: 0.011
Method: Least Squares F-statistic: 3.634
Date: Fri, 16 Jan 2026 Prob (F-statistic): 0.0578
Time: 12:07:31 Log-Likelihood: -423.13
No. Observations: 244 AIC: 850.3
Df Residuals: 242 BIC: 857.3
Df Model: 1
Covariance Type: nonrobust
=====================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------
Intercept 2.7281 0.167 16.347 0.000 2.399 3.057
C(time)[T.Dinner] 0.3746 0.197 1.906 0.058 -0.012 0.762
==============================================================================
Omnibus: 77.962 Durbin-Watson: 1.958
Prob(Omnibus): 0.000 Jarque-Bera (JB): 206.982
Skew: 1.437 Prob(JB): 1.13e-45
Kurtosis: 6.479 Cond. No. 3.56
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Die Auswertung des linearen Modells gibt Aufschluss über die Mittelwertdifferenzen im Vergleich zur Referenzruppe. Der Intercept der in der letzten Tabelle zeigt beispielsweise, dass das durchschnittliche Trinkgeld in der Referenzgruppe (Lunch) bei 2.7281 liegt und in der zweiten Gruppe (Dinner) durchschnittlich um 0.3746 höher ist. Allerdings ist dieser Unterschied, wie bereits bei der ANOVA_Auswertung gesehen, nicht statistisch signifikant, da der p-Value für den Test nicht ausreicht, um die Nullhypothese \(H_0: \, \beta_1=0 \Leftrightarrow \mu_2 = \mu_1\) bei 5%-iger Irrtumswahrscheinlichkeit zu verwerfen.
8.8.3. ANOVA vs. lineare Regression#
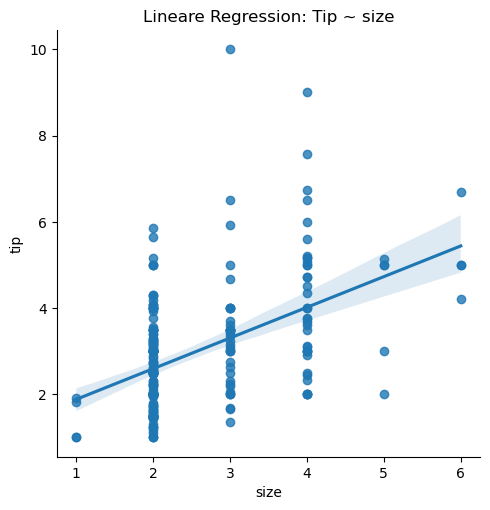
Sowohl die klassischen Regressionsmodelle als auch die ANOVA zählen zu den linearen Modellen und können somit auch in Python nahezu identisch umgesetzt werden. Allerdings soll am Beispiel der Analyse vom Einfluss der Tischgröße auf das Trinkgeld kurz der Unterschied zwischen beiden Verfahren nochmals veranschaulicht werden. Die Prognose im Falle der einfachen lineare Regression \(\hat y = \hat a + \hat b x = 1.1691 + 0.7118 x\) zeigt, dass sich mit jedem zusätzlichen Gast am Tisch das durchschnittliche Trinkgeld um \(0.7118\) Dollar erhöht.
# einfache lineare Regression: Trinkgeld ~ Tischgroesse
sns.lmplot(data=tips, x="size", y="tip")
plt.title("Lineare Regression: Tip ~ size")
plt.show()
/HOME1/users/personal/dana/miniconda3/envs/finance/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
#Standard Regression mit metrischer Variable size
model1 = ols("tip ~ size", data=tips).fit()
anova_table1 = sm.stats.anova_lm(model1, typ=1)
print(anova_table1)
print(model1.summary())
df sum_sq mean_sq F PR(>F)
size 1.0 111.378050 111.378050 76.175426 4.300543e-16
Residual 242.0 353.834427 1.462126 NaN NaN
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.239
Model: OLS Adj. R-squared: 0.236
Method: Least Squares F-statistic: 76.18
Date: Fri, 16 Jan 2026 Prob (F-statistic): 4.30e-16
Time: 12:07:31 Log-Likelihood: -391.56
No. Observations: 244 AIC: 787.1
Df Residuals: 242 BIC: 794.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.1691 0.223 5.233 0.000 0.729 1.609
size 0.7118 0.082 8.728 0.000 0.551 0.872
==============================================================================
Omnibus: 81.369 Durbin-Watson: 1.820
Prob(Omnibus): 0.000 Jarque-Bera (JB): 273.339
Skew: 1.393 Prob(JB): 4.42e-60
Kurtosis: 7.373 Cond. No. 8.85
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Die Testgröße der zuhörigen Varianzanalyse, die \(H_0: \, \beta_1=b = 0\) testet, beträgt \(f=76.18=8.728^2\) und führt zu einem extrem kleinen p-Value, so dass wir hier den signifikanten Nachweis der Alternativhypothese \(H_1: \beta_1 = b \neq 0\) haben.
Obige Graphik zeigt allerdings, dass die Anzahl der Gäste ein diskretes Merkmal ist, welches wir auch als katgorielle Variable interpretieren können und somit eine ANOVA durchführen können, um zu untersuchen, ob sich das mittlere Trinkgeld über die verschiedenenen Gruppen unterscheidet.
Genauer lautet für die klassische ANOVA die Nullhypothese \(H_0: \, \mu_1 = \mu_2 = \ldots \mu_6\). Der folgende Boxplot zeigt, dass die Daten nicht für diese Hypothese sprechen.
Der Python-Code zur Berechnung des 2. Modells unterscheidet sich nur durch die Kodierung, dass die Variable size durch C(size) als Faktor interpretiert werden soll.
tips.boxplot(column="tip", by="size")
tips.groupby("size")["tip"].agg(
count="count",
mean="mean",
median="median",
std="std",
var="var",
)
| count | mean | median | std | var | |
|---|---|---|---|---|---|
| size | |||||
| 1 | 4 | 1.437500 | 1.415 | 0.506516 | 0.256558 |
| 2 | 156 | 2.582308 | 2.500 | 0.985501 | 0.971213 |
| 3 | 38 | 3.393158 | 3.290 | 1.557344 | 2.425319 |
| 4 | 37 | 4.135405 | 3.760 | 1.640668 | 2.691792 |
| 5 | 5 | 4.028000 | 5.000 | 1.440111 | 2.073920 |
| 6 | 4 | 5.225000 | 5.000 | 1.053170 | 1.109167 |
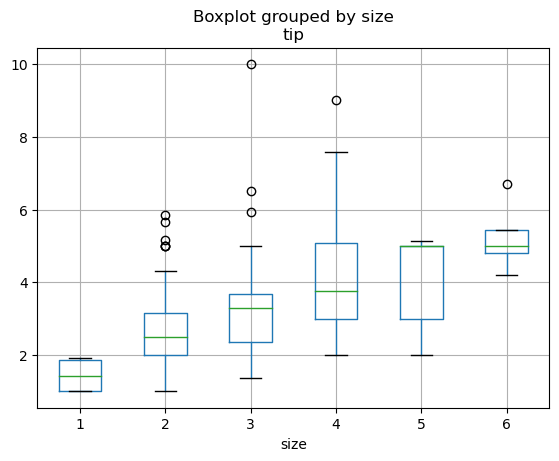
#Anova = Regression mit dummy-Variablen fuer kategorielle Daten (1. Kategorie (size = 1)) als Referenzgruppe
model2 = ols("tip ~ C(size)", data=tips).fit()
anova_table2 = sm.stats.anova_lm(model2, typ=1)
print(anova_table2)
print(model2.summary())
df sum_sq mean_sq F PR(>F)
C(size) 5.0 115.640313 23.128063 15.746331 2.169463e-13
Residual 238.0 349.572164 1.468791 NaN NaN
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.249
Model: OLS Adj. R-squared: 0.233
Method: Least Squares F-statistic: 15.75
Date: Fri, 16 Jan 2026 Prob (F-statistic): 2.17e-13
Time: 12:07:31 Log-Likelihood: -390.09
No. Observations: 244 AIC: 792.2
Df Residuals: 238 BIC: 813.2
Df Model: 5
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept 1.4375 0.606 2.372 0.018 0.244 2.631
C(size)[T.2] 1.1448 0.614 1.865 0.063 -0.064 2.354
C(size)[T.3] 1.9557 0.637 3.070 0.002 0.701 3.211
C(size)[T.4] 2.6979 0.638 4.229 0.000 1.441 3.955
C(size)[T.5] 2.5905 0.813 3.186 0.002 0.989 4.192
C(size)[T.6] 3.7875 0.857 4.420 0.000 2.099 5.476
==============================================================================
Omnibus: 77.409 Durbin-Watson: 1.807
Prob(Omnibus): 0.000 Jarque-Bera (JB): 244.825
Skew: 1.344 Prob(JB): 6.87e-54
Kurtosis: 7.106 Cond. No. 24.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Der Testwert des Fisher-Tests ist im 2. Modell \(f=15.75\) und führt ebenso zur Verwerfung der Nullhypothese und somit zum signifikanten Nachweis der Alternativhypothese, dass sich mind. ein Unterschied zwischen den Gruppen findet. Eine Auswertung des linearen Modells zeigt mit \(\hat \beta_0 = \hat\mu_1 = 1.4375\) das durchschnittliche Trinkgeld für einzelne Gäste an. Die restlichen Koeffizienten \(\hat \beta_k = \hat \mu_{k+1} - \hat \mu_1 = \hat \alpha_{k+1} - \hat \alpha_1\) für \(k=1, \ldots,5\) zeigt hingegen die Unterschiede der jeweils \(k+1\) zur 1. Referenzgruppe auf. Die zugeöhrigen Tests mit \(H_0: \, \beta_k = 0 \Leftrightarrow \mu_{k+1} = \mu_1 \Leftrightarrow \alpha_{k+1} = \alpha_1\) fallen alle signifikant aus, so dass hier der statistische Nachweis, dass sich alle Gruppenmittel (2er Tisch, 3er Tisch, .. , 6er Tisch) sich vom durchschnittlichen Trinkgeld von 1er Tischen unterscheiden. Beide Modelle untersuchen demnach ähnliche, aber prinzipiell verschiedene Fragestellungen mit entsprechend unterschiedlichen Hypothesen. Ein Vergleich der Designmatrizen sowie der Freiheitsgrade beider Modelle verdeutlicht dies nochmals.
8.8.3.1. Vergleich der Designmatrizen#
X1_design = model1.model.exog
N1, m1 = X1_design.shape
print("lineare Regression Modell-Dimension: N=%s (sample size), m=%s (model)" % (N1,m1))
print("Freiheitsgrade (df):\ndf_resid:", model1.df_resid, " = N - m =", N1 - m1, "df_model:", model1.df_model, "= m-1 =",m1-1)
print(X1_design[:10])
lineare Regression Modell-Dimension: N=244 (sample size), m=2 (model)
Freiheitsgrade (df):
df_resid: 242.0 = N - m = 242 df_model: 1.0 = m-1 = 1
[[1. 2.]
[1. 3.]
[1. 3.]
[1. 2.]
[1. 4.]
[1. 4.]
[1. 2.]
[1. 4.]
[1. 2.]
[1. 2.]]
X2_design = model2.model.exog
N2, m2 = X2_design.shape
print("ANOVA Modell-Dimension: N=%s (sample size), m=%s (model)" % (N2,m2))
print("Freiheitsgrade (df):\ndf_resid:", model2.df_resid, " = N - m =", N2 - m2, "df_model:", model2.df_model, "= m-1 =",m1-1)
print(X2_design[:10])
ANOVA Modell-Dimension: N=244 (sample size), m=6 (model)
Freiheitsgrade (df):
df_resid: 238.0 = N - m = 238 df_model: 5.0 = m-1 = 1
[[1. 1. 0. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[1. 1. 0. 0. 0. 0.]
[1. 0. 0. 1. 0. 0.]
[1. 0. 0. 1. 0. 0.]
[1. 1. 0. 0. 0. 0.]
[1. 0. 0. 1. 0. 0.]
[1. 1. 0. 0. 0. 0.]
[1. 1. 0. 0. 0. 0.]]
Wie üblich gibt es natürlich mehrere Möglichkeiten sich die Designmatrix zu erstellen und wir zeigen hier eine Alternative
import patsy
y_Data, Design = patsy.dmatrices("tip ~ size", data=tips)
#print(y_Data)
print(Design[:10])
[[1. 2.]
[1. 3.]
[1. 3.]
[1. 2.]
[1. 4.]
[1. 4.]
[1. 2.]
[1. 4.]
[1. 2.]
[1. 2.]]
Mittels der Treatment() Option, kann die Referenzgruppe auch einfach angepasst werden, dann ändert sich insbesondere das lineare Modell, da sich Koeffizienten-Vektor und Designmatrix ändern und folglich auch die untersuchten Hypothesen anpassen.
model2_b = ols("tip ~ C(size, Treatment(reference=4))", data=tips).fit()
print(model2_b.summary())
print(model2_b.model.exog[:10])
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.249
Model: OLS Adj. R-squared: 0.233
Method: Least Squares F-statistic: 15.75
Date: Fri, 16 Jan 2026 Prob (F-statistic): 2.17e-13
Time: 12:07:31 Log-Likelihood: -390.09
No. Observations: 244 AIC: 792.2
Df Residuals: 238 BIC: 813.2
Df Model: 5
Covariance Type: nonrobust
========================================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------------------
Intercept 4.1354 0.199 20.756 0.000 3.743 4.528
C(size, Treatment(reference=4))[T.1] -2.6979 0.638 -4.229 0.000 -3.955 -1.441
C(size, Treatment(reference=4))[T.2] -1.5531 0.222 -7.008 0.000 -1.990 -1.117
C(size, Treatment(reference=4))[T.3] -0.7422 0.280 -2.652 0.009 -1.294 -0.191
C(size, Treatment(reference=4))[T.5] -0.1074 0.577 -0.186 0.853 -1.245 1.030
C(size, Treatment(reference=4))[T.6] 1.0896 0.638 1.708 0.089 -0.167 2.346
==============================================================================
Omnibus: 77.409 Durbin-Watson: 1.807
Prob(Omnibus): 0.000 Jarque-Bera (JB): 244.825
Skew: 1.344 Prob(JB): 6.87e-54
Kurtosis: 7.106 Cond. No. 11.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[[1. 0. 1. 0. 0. 0.]
[1. 0. 0. 1. 0. 0.]
[1. 0. 0. 1. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0. 0.]
[1. 0. 0. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]]
Der folgende Code zeigt den Einfluss des Modells, welcher durch die Eränzung -1 in der Formel den Intercept entfernt. Dann entsprechen die Koeffizienten nur noch den Gruppenmittelwerten \(\beta_k=\mu_k\) und die Auswertung des linearen Modelles passt sich entsprechend an.
model_2c = ols("tip ~ C(size) - 1", data=tips).fit()
print(model_2c.summary())
print(model_2c.model.exog[:10])
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.249
Model: OLS Adj. R-squared: 0.233
Method: Least Squares F-statistic: 15.75
Date: Fri, 16 Jan 2026 Prob (F-statistic): 2.17e-13
Time: 12:07:32 Log-Likelihood: -390.09
No. Observations: 244 AIC: 792.2
Df Residuals: 238 BIC: 813.2
Df Model: 5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
C(size)[1] 1.4375 0.606 2.372 0.018 0.244 2.631
C(size)[2] 2.5823 0.097 26.613 0.000 2.391 2.773
C(size)[3] 3.3932 0.197 17.259 0.000 3.006 3.780
C(size)[4] 4.1354 0.199 20.756 0.000 3.743 4.528
C(size)[5] 4.0280 0.542 7.432 0.000 2.960 5.096
C(size)[6] 5.2250 0.606 8.623 0.000 4.031 6.419
==============================================================================
Omnibus: 77.409 Durbin-Watson: 1.807
Prob(Omnibus): 0.000 Jarque-Bera (JB): 244.825
Skew: 1.344 Prob(JB): 6.87e-54
Kurtosis: 7.106 Cond. No. 6.24
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[[0. 1. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]]
Zu beachten ist, dass die Varianzzerlegung, welche den Einfluss des Faktors auf die zu erklärente Variable \(Y\) untersucht, von der konkreten Dummy-Kodierung und somit Modellwahl unabhängig ist.
8.8.4. Mehrfaktorielle ANOVA#
Möchte man mehrere Faktoren im Modell berücksichtigen, wird eine mehrfaktorielle Varianzanalyse angewendet, die zusätzliche noch die Wechselwirkungen (Interaktionen) zwischen den Faktoren berücksichtigen kann, welche in der Regel allerdings, die Interpretierbarkeit deutlich verkompliziert, falls sie tatsächliche vorhanden sind. Dies soll allerdings hier nicht weiter thematisiert werden.
Beim Formulieren eines statistischen Modells zur Vorhersage von \(Y \sim Var1 + Var2 + C(A) + C(B) + C(A)*C(B) + \ldots\) können wir nun natürlich sowohl kategorielle Variablen (Faktoren) als auch metrische Variablen und deren Transformationen sowie die Interaktionen zwischen den einzelnen Variablen berücksichtigen. Das + in der Formel wird immer als ein additives Hinzufügen zum Modell interpretiert, während der Oprator * als Interaktionsoperator zu verstehen ist. Möchte man beispielsweise eine quadrierte Variable \(x^2\) bzw. \(\log(x)\) im Modell berücksichtigen, ergänzt man die Formel um \(I(x**2)\) bzw. \(np.log(x)\). Somit ist die Umsetzung komplexer linearer Modelle sehr einfach zu implemntieren.
Dies beeinflusst natürlich die Designmatrix sowie den Koeffizientenvektor und folglich auch die zugehörigen Tests für \(\beta=0\). Insbesondere Interaktionenen verkomplizeren allerdings die Interpretationen der Koeffizientenauswertungen und wir verweisen an dieser Stelle auf die Literatur, z.B. [11] ( Link)
In der Finance-Literatur wird fast nie von einer ANOVA gesprochen, sondern weil die ANOVA ein Spezialfall eines linearen Modells darstellt einfach nur von Linearen Faktor-Modellen mit Interaktionen gesprochen.
# Vollständiges Modell mit Interaktionen
model_full1 = ols(
"tip ~ total_bill + size + C(time) + C(day) + C(day)*C(time)",
data=tips
).fit()
print(model_full1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: tip R-squared: 0.469
Model: OLS Adj. R-squared: 0.454
Method: Least Squares F-statistic: 29.82
Date: Fri, 16 Jan 2026 Prob (F-statistic): 2.45e-29
Time: 12:07:32 Log-Likelihood: -347.64
No. Observations: 244 AIC: 711.3
Df Residuals: 236 BIC: 739.3
Df Model: 7
Covariance Type: nonrobust
===================================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------------------------
Intercept 0.6621 0.221 2.995 0.003 0.227 1.098
C(time)[T.Dinner] 0.2142 1.032 0.208 0.836 -1.819 2.248
C(day)[T.Fri] 0.1500 0.410 0.366 0.715 -0.658 0.958
C(day)[T.Sat] -0.1292 0.515 -0.251 0.802 -1.143 0.885
C(day)[T.Sun] -0.0737 0.516 -0.143 0.886 -1.090 0.942
C(day)[T.Fri]:C(time)[T.Dinner] -0.3234 1.141 -0.283 0.777 -2.572 1.925
C(day)[T.Sat]:C(time)[T.Dinner] -0.1292 0.515 -0.251 0.802 -1.143 0.885
C(day)[T.Sun]:C(time)[T.Dinner] -0.0737 0.516 -0.143 0.886 -1.090 0.942
total_bill 0.0932 0.009 9.974 0.000 0.075 0.112
size 0.1870 0.088 2.132 0.034 0.014 0.360
==============================================================================
Omnibus: 25.810 Durbin-Watson: 2.097
Prob(Omnibus): 0.000 Jarque-Bera (JB): 48.438
Skew: 0.566 Prob(JB): 3.03e-11
Kurtosis: 4.867 Cond. No. 5.97e+17
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 3.28e-31. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
8.9. Regression für Zeitreihen (to do)#
Achtung: die Annahmen von unabhängigen und identisch verteilten Residuen für obige lineare Modelle ist für Zeitreihen im Allgemeinen nicht mehr gegeben. Sowohl die Zeitabhängigkeit als auch Nichtstationarität müssen entsprechend gehandelt werden. Häufig ist es sinnvoll die Zeitreihen beispielsweise durch Differenzenbildung in stationäre Zeitreihen zu überführen. Dies haben wir auch beim Übergang vpn Aktienkursen zu Renditen bzw. Returns durchgeführt. Außerdem sollte immer eine Analyse der Autokovarianzfunktion vor der Regression durchgeführt werden.
