Weitere Grafiken mit Matplotlib#
Stellen wir den Fehlerverlauf in einem kartesischen Koordinatensystem und einem Koordinatensystem mit logarithmischer y-Achse dar:
import math
import numpy as np
import matplotlib.pyplot as plt
n = np.array(range(1,6), dtype='float64')
err_p1 = (0.8)**n
err_p2 = [1./math.factorial(int(i)) for i in n]
err_p3 = (0.8)**(2**n)
plt.figure(figsize=(10,5))
def generate_plot():
plt.plot(n, err_p1, 'ro-', label='Q-linear')
plt.plot(n, err_p2, 'bo-', label='Q-superlinear')
plt.plot(n, err_p3, 'co-', label='Q-quadratisch')
plt.grid()
# Plot in kartesischen Koordinatensystem
plt.subplot(1,2,1)
generate_plot()
plt.legend(loc='upper right')
# Plot in Koordinatensystem mit logarithmischer y-Achse
plt.subplot(1,2,2)
generate_plot()
plt.semilogy()
plt.legend(loc='lower left')
plt.show()
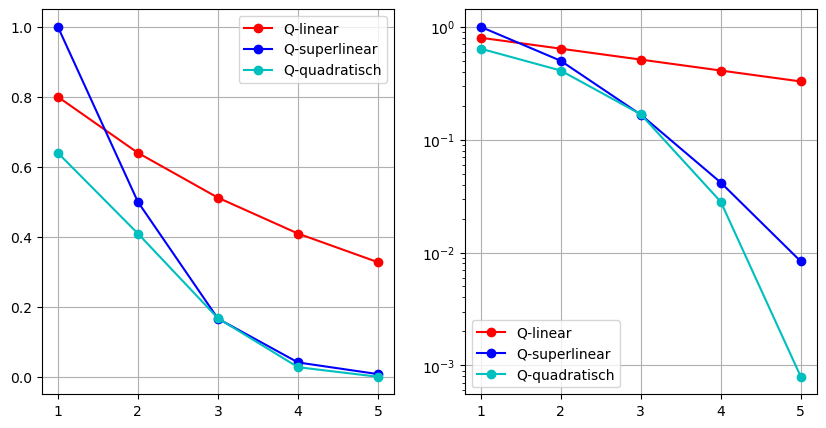
Wir sehen, dass eine \(Q\)-linear konvergente Folge im Plot mit logarithmischer y-Achse einer lineare Funktion ist.
Analog dazu kann man auch die \(x\)-Achse mit plt.semilogx() logatithmisch skalieren, was bei oben vorgestellter Anwendung allerdings wenig Sinn macht.
Balken-, Linien- und Kuchendiagramme#
Schauen wir uns weitere elementare Plot-Typen an. Angenommen wir haben die Auswertung einer Umfrage vorliegen, und möchten diese graphisch aufbereiten. Unsere Beispieldaten sind:
Erstellung der Farbpalette#
Dieser Python-Code verwendet die Bibliotheken matplotlib.pyplot und matplotlib.colors, um eine übersichtliche Visualisierung verschiedener Farbpaletten in Tabellenform zu erstellen. Mit Hilfe einer zentralen Funktion namens plot_colortable werden Farbnamen und ihre entsprechenden Farbfelder grafisch dargestellt. Der Code zeigt dabei exemplarisch drei verschiedene Farbsets: die Grundfarben (BASE_COLORS), die Tableau-Palette (TABLEAU_COLORS) sowie die CSS4-Farben (CSS4_COLORS), die allesamt vordefinierte Farbnamen aus Matplotlibs Farbsystem sind. Optional ließe sich auch die sehr umfangreiche XKCD-Farbsammlung darstellen, was allerdings eine sehr große Grafik erzeugen würde.
Praktisch ist dieser Code besonders nützlich, wenn man sich einen schnellen Überblick über verfügbare Farben und deren Namen verschaffen möchten – etwa bei der Auswahl konsistenter Farben für Diagramme, Benutzeroberflächen oder Präsentationen. Die Farben können alphabetisch oder nach Farbwerten sortiert angezeigt werden, was eine einfache Orientierung innerhalb großer Farbsammlungen ermöglicht.
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
def plot_colortable(colors, title, sort_colors=True, emptycols=0):
cell_width = 212
cell_height = 22
swatch_width = 48
margin = 12
topmargin = 40
# Sort colors by hue, saturation, value and name.
if sort_colors is True:
by_hsv = sorted((tuple(mcolors.rgb_to_hsv(mcolors.to_rgb(color))),
name)
for name, color in colors.items())
names = [name for hsv, name in by_hsv]
else:
names = list(colors)
n = len(names)
ncols = 4 - emptycols
nrows = n // ncols + int(n % ncols > 0)
width = cell_width * 4 + 2 * margin
height = cell_height * nrows + margin + topmargin
dpi = 72
fig, ax = plt.subplots(figsize=(width / dpi, height / dpi), dpi=dpi)
fig.subplots_adjust(margin/width, margin/height,
(width-margin)/width, (height-topmargin)/height)
ax.set_xlim(0, cell_width * 4)
ax.set_ylim(cell_height * (nrows-0.5), -cell_height/2.)
ax.yaxis.set_visible(False)
ax.xaxis.set_visible(False)
ax.set_axis_off()
ax.set_title(title, fontsize=24, loc="left", pad=10)
for i, name in enumerate(names):
row = i % nrows
col = i // nrows
y = row * cell_height
swatch_start_x = cell_width * col
text_pos_x = cell_width * col + swatch_width + 7
ax.text(text_pos_x, y, name, fontsize=14,
horizontalalignment='left',
verticalalignment='center')
ax.add_patch(
Rectangle(xy=(swatch_start_x, y-9), width=swatch_width,
height=18, facecolor=colors[name], edgecolor='0.7')
)
return fig
plot_colortable(mcolors.BASE_COLORS, "Grundfarben",
sort_colors=False, emptycols=1)
plot_colortable(mcolors.TABLEAU_COLORS, "Tableau-Palette",
sort_colors=False, emptycols=2)
plot_colortable(mcolors.CSS4_COLORS, "CSS-Farben")
# Optionally plot the XKCD colors (Caution: will produce large figure)
# xkcd_fig = plot_colortable(mcolors.XKCD_COLORS, "XKCD Colors")
# xkcd_fig.savefig("XKCD_Colors.png")
plt.show()



Plots für Skalar- und Vektorfelder#
Auch für die graphische Darstellung von Skalarfeldern \(f\colon \mathbb{R}^2 \to \mathbb{R}\) und Vektorfeldern \(\vec F\colon \mathbb{R}^2 \to \mathbb{R}^2\) stehen einige Funktionen in Matplotlib bereit. Die meisten Funktionen zur Darstellung von Skalarfeldern erwarten als Argument 3 Matrizen, eine für die \(x\)-Koordinaten, eine für die \(y\)-Koordinaten und eine für den Funktionswert \(f(x,y)\). Hilfreich ist hier die Funktion numpy.meshgrid mit der wir ein 2D-Tensorprodukt-Gitter aus 2 1D-Gittern erzeugen:
# 1D-Gitter für x- und y-Variable
x = np.linspace(-4.5,3.5,1001)
y = np.linspace(-3.5,3.5,1001)
# 2D-Gitter erzeugen
X,Y = np.meshgrid(x,y)
# Definiere Himmelblau-Funktion
Z = (X**2 + y - 11)**2 + (X + Y**2 - 7)**2
Eine mögliche Darstellung einer solchen Funktion wäre ein Contour-Plot, in welchem die Kurven \(\{(x,y)\colon f(x,y)=c_i\}\) für verschiedene Werte \(c_1<c_2 < \ldots<c_{\text{levels}}\) eingezeichnet werden:
plt.contour(X,Y,Z, levels=25)
plt.colorbar()
plt.show()
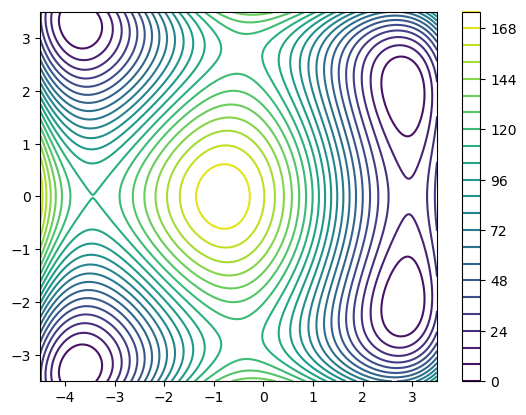
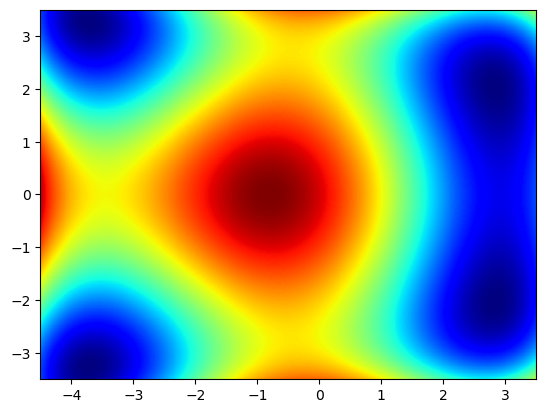
Ähnlich funktionieren Color-Plots, bei denen der Funktionswert an einer Stelle \((x,y)\) dem Farbwert einer vordefinierten Farbpalette entspricht:
import matplotlib.cm as cm
plt.pcolormesh(X,Y,Z, cmap=cm.jet)
plt.show()
Skalarfelder lassen sich auch in dreidimensionalen Koordinatensystemen darstellen. Die Argumente werden auf \(x\)- und \(y\)-Achse aufgetragen, und der Funktionswert auf die \(z\)-Achse. Die entsprechenden Plot-Befehle sind allerdings nicht im Submodul matplotlib.pyplot definiert, daher müssen wir einen Umweg nehmen. Zunächst erzeugen wir uns ein Bildobjekt mit
fig = plt.figure()
fügen ein 3D-Koordinatensystem hinzu
ax = fig.axes(projection='3d')
und nutzen die vom Objekt ax bereitgestellten Plot-Befehle. Hier ein Beispiel:
plt.figure(figsize=(8,6))
# 3D-Koordinatensystem hinzufügen
ax = plt.axes(projection='3d')
# Surface-Plot erstellen
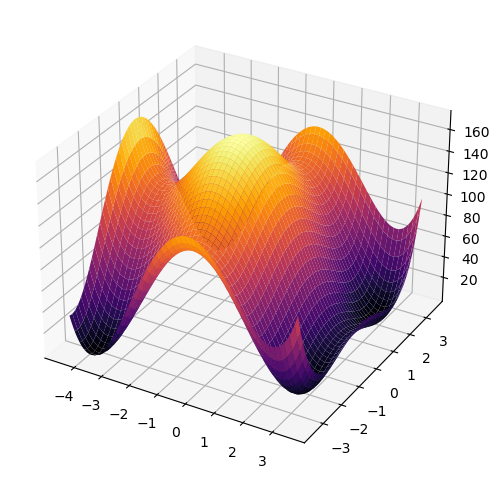
ax.plot_surface(X,Y,Z, cmap=cm.inferno)
plt.show()
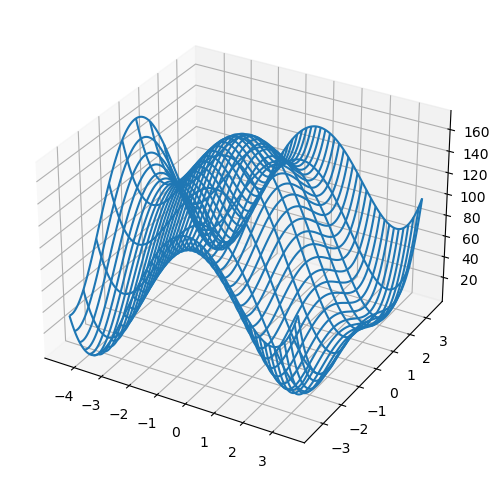
plt.figure(figsize=(8,6))
ax = plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z, rcount=10)
plt.show()
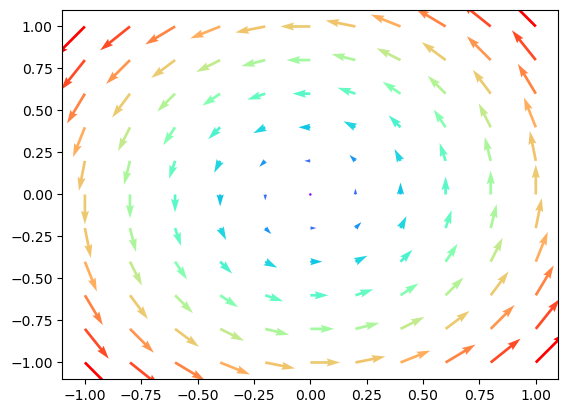
Schauen wir uns noch eine Methode mit der wir Vektorfelder zeichnen können. Als Beispiel definieren wir \(\vec f(x,y) = (-y,x)^\top\). Solche Vektorfelder können in sogenannten Quiver-Plots dargestellt werden:
x = np.linspace(-1,1, 11)
y = np.linspace(-1,1, 11)
# Punktgitter definieren
X,Y = np.meshgrid(x, y)
# Funktionswerte von F
Z1 = -Y
Z2 = X
# Optional: Färbe Pfeile nach Länge
C = np.sqrt(Z1**2 + Z2**2)
# Quiverplot erzeugen und anzeigen
plt.quiver(X, Y, Z1, Z2, C, cmap=cm.rainbow)
plt.show()
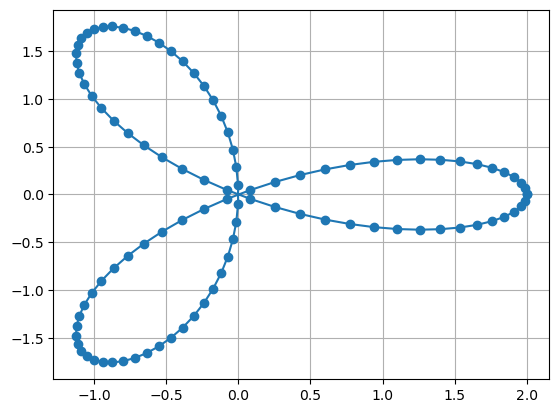
Auch Kurven lassen sich in Matplotlib zeichnen. Eine Kurve ist zunächst eine Menge an Punkten
mit einer sogenannten Kurvenparametrisierung \(\vec x\colon[t_a,t_b]\to\mathbb{R}^n\), welche regulär ist, d.h., \(\dot{\vec x}(t)\ne 0\) für alle \(t\in [t_a,t_b]\). Für eine ebene Kurve (\(n=2\)) können wir den normalen Plot-Befehl nutzen. Das Kleeblatt
zeichnen wir beispielsweise mit
t = np.linspace(0,2*np.pi,100)
x = np.cos(t)+np.cos(2*t)
y = np.sin(t)-np.sin(2*t)
plt.plot(x,y,'o-')
plt.grid()
plt.show()
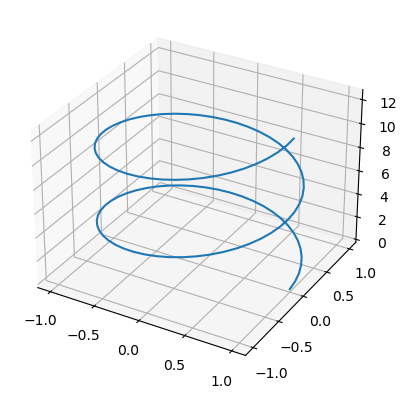
Ähnlich kann man Raumkurven (\(n=3\)) zeichnen, man benötigt nur vorher ein dreidimensionales Koordinatensystem. Wie wir das anlegen haben wir aber schon gesehen. Wir zeichnen hier die Schraubenlinie
t = np.linspace(0,4*np.pi,100)
x = np.cos(t)
y = np.sin(t)
z = t
ax = plt.axes(projection='3d')
ax.plot3D(x, y, z)
plt.show()