Erstellung von Graphiken mittels Matplotlib, Seaborn und Plotly#
Matplotlib ist eine mächtige Python-Bibliothek, welche viele Funktionen für die graphische Darstellung in Form von Plots und Diagrammen bereitstellt. Wir werden in diesem Abschnitt die grundlegende Funktionsweise kennenlernen. Sehr viele neuere Graphik-Pakete bauen auf diesem Basispaket auf und erleichtern die Erstellung von Graphiken oder erweitern den Funktionsumfang. So können mit Plotly, welches Bestandteil des Matplotlib-Pakets ist, interaktive Graphiken erstellt werden und mit Seaborn insbesondere klassiche statistische Plots sehr komfortabel erstellt werden.
Visualisierungen mit Matplotlib#
Matplotlib bietet zwei verschiedene Arbeitsweisen, um Diagramme zu erstellen: das state-based Interface über pyplot und das object-oriented Interface mit Figure und Axes.
Das state-based Interface (plt) funktioniert so, dass Matplotlib im Hintergrund immer ein „aktuelles“ Diagramm verwaltet. Befehle wie plt.plot() oder plt.title() wirken automatisch auf dieses aktive Diagramm. Das ist sehr praktisch für schnelle Visualisierungen, weil man mit wenigen Befehlen sofort ein Ergebnis erhält. Allerdings wird es schnell unübersichtlich, sobald man mehrere Diagramme oder komplexere Layouts darstellen möchte, da man nicht immer genau im Blick hat, auf welches Objekt sich der jeweilige Befehl gerade bezieht.
Das object-oriented Interface arbeitet hingegen explizit mit Objekten. Man erstellt eine Figur (Figure) und darin ein oder mehrere Achsen (Axes). Auf diese Objekte ruft man dann Methoden wie ax.plot() oder ax.set_title() auf. Der große Vorteil liegt darin, dass man immer genau weiß, welches Element man verändert, und dass sich die Struktur bei mehreren Subplots oder komplexen Darstellungen viel besser kontrollieren lässt. Der Nachteil ist lediglich, dass der Code etwas ausführlicher wirkt.
Zusammengefasst kann man sagen: Für schnelle und einfache Plots ist das state-based Interface völlig ausreichend. Für größere Projekte, Publikationen oder Layouts mit mehreren Teilplots empfiehlt sich das object-oriented Interface, da sie deutlich sauberer und flexibler ist.
Ähnlich wie bei NumPy müssen wir Matplotlib und Seaborn erst installieren. Dies erledigt man in seiner Umgebung mit folgendem Befehl:
conda install -c conda-forge matplotlib
pip install matplotlib
Anschließend können wir Matplotlib, besser gesagt das Submodul matplotlib.pyplot in unser Programm einbinden:
import matplotlib.pyplot as plt
State-based Interface#
Der wichtigste Befehl ist plt.plot(). Wir geben plt.plot? ein um zu erfahren wie dieser funktioniert. In der einfachsten Form sind die Argumente dieser Funktion 2 Vektoren mit x- bzw. y-Koordinaten einer Punktwolke. Diese Vektoren können Listen, oder Numpy-Arrays sein. Die Sinusfunktion können wir wie folgt plotten:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2*np.pi, 11) # Erzeuge Gitter [0, 0.2*pi, 0.4*pi, ..., 2*pi])
y = np.sin(x) # Berechne zugehörige Funktionswerte
plt.plot(x,y) # Erzeuge Plot
plt.show() # Zeige den Plot
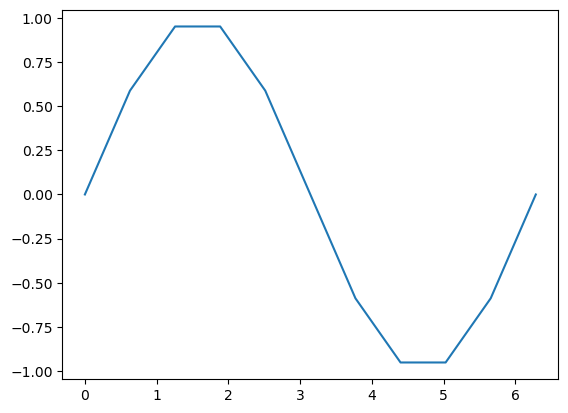
Hier sehen wir auch eine schöne Anwendung der komponentenweise definierten mathematischen Funktionen aus numpy.
Übungsaufgabe
Plotte die Funktion \(f(x) = e^{-x}\,\sin(2\,\pi\,x)\) im Intervall \([0,6]\).
Gestaltung von Plots#
Machen wir unseren Plot noch etwas schöner:
import numpy as np
x = np.linspace(0,4*np.pi, 1001) # Erzeuge äquidistantes Gitter für das Intervall [0, 4*pi]
y = np.sin(x) # Berechne zugehörige Funktionswerte für sinus
z = np.cos(x) # und cosinus
plt.figure(figsize=(10,5)) # Größe einstellen
plt.plot(x,y,label="$\sin(x)$") # Erzeuge Plot für Sinus
plt.plot(x,z,label="$\cos(x)$") # Erzeuge Plot für Cosinus
plt.title("Sinus und Cosinus") # Titel des Plots
plt.grid() # Gitterlinien einschalten
plt.xlabel('x') # Bezeichner an x-Achse
plt.ylabel('f(x)') # Bezeichner an y-Achse (in Latex-Code)
plt.legend() # Legende
plt.show() # Zeige den Plot
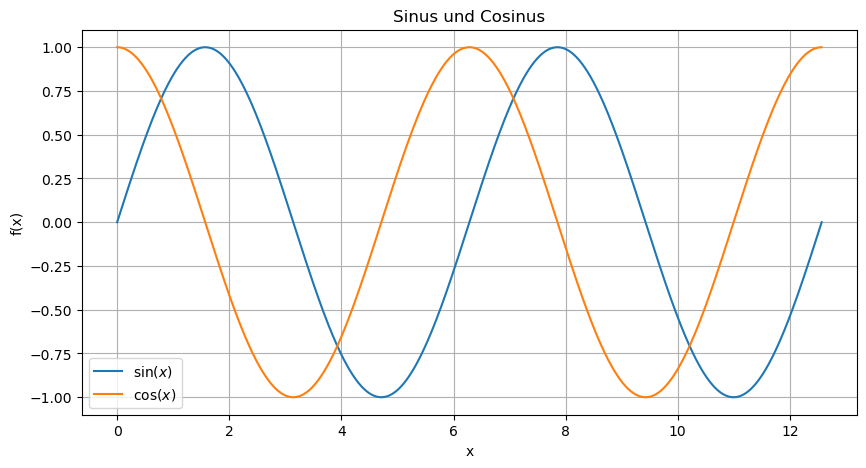
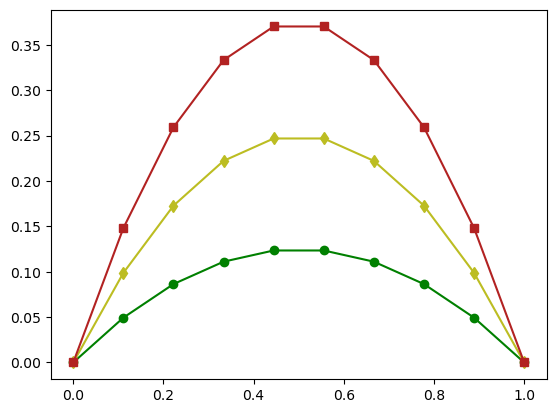
Im Prinzip hat Matplotlib unsere Punktwolke mit Koordinaten aus x und y gezeichnet, und die Punkte mit Linen verbunden. Es gibt aber noch einige andere Linientypen:
x = np.linspace(0,2,21)
y1= x-0.5*x**2
y2= 2*x-x**2
y3= 3*x-1.5*x**2
plt.figure(figsize=(10,5)) # Größe einstellen
# Zeichne rote (r) Kreise (o) mit Verbindungslinien (-)
plt.plot(x, y1, 'ro-', linewidth=0.2, label='f1')
# Zeichne blaue (b) Quadrate (s)
plt.plot(x, y2, 'bs', label='f1')
# Zeichne cyane (c) Dreiecke (^) mit gestrichelten Verbindungslinien (--)
plt.plot(x, y3, 'c^--', markersize=10, label='f1')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()
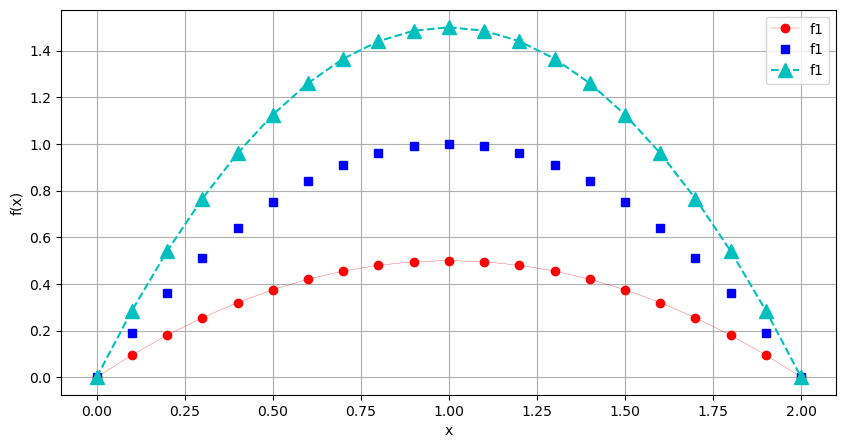
Im Hilfetext plt.plot? sind noch weitere Linien- und Markertypen erklärt. Vordefinierte Farben im Submodul matplotlib.colors. Es gibt verschiedene Farbpaletten. Die Grundfarben sind:
import matplotlib.colors as mcolors
mcolors.BASE_COLORS
{'b': (0, 0, 1),
'g': (0, 0.5, 0),
'r': (1, 0, 0),
'c': (0, 0.75, 0.75),
'm': (0.75, 0, 0.75),
'y': (0.75, 0.75, 0),
'k': (0, 0, 0),
'w': (1, 1, 1)}
Es gibt weiterhin die Farbpalette Tableau:
mcolors.TABLEAU_COLORS
{'tab:blue': '#1f77b4',
'tab:orange': '#ff7f0e',
'tab:green': '#2ca02c',
'tab:red': '#d62728',
'tab:purple': '#9467bd',
'tab:brown': '#8c564b',
'tab:pink': '#e377c2',
'tab:gray': '#7f7f7f',
'tab:olive': '#bcbd22',
'tab:cyan': '#17becf'}
Und außerdem noch CSS-Farben:
mcolors.CSS4_COLORS
{'aliceblue': '#F0F8FF',
'antiquewhite': '#FAEBD7',
'aqua': '#00FFFF',
'aquamarine': '#7FFFD4',
'azure': '#F0FFFF',
'beige': '#F5F5DC',
'bisque': '#FFE4C4',
'black': '#000000',
'blanchedalmond': '#FFEBCD',
'blue': '#0000FF',
'blueviolet': '#8A2BE2',
'brown': '#A52A2A',
'burlywood': '#DEB887',
'cadetblue': '#5F9EA0',
'chartreuse': '#7FFF00',
'chocolate': '#D2691E',
'coral': '#FF7F50',
'cornflowerblue': '#6495ED',
'cornsilk': '#FFF8DC',
'crimson': '#DC143C',
'cyan': '#00FFFF',
'darkblue': '#00008B',
'darkcyan': '#008B8B',
'darkgoldenrod': '#B8860B',
'darkgray': '#A9A9A9',
'darkgreen': '#006400',
'darkgrey': '#A9A9A9',
'darkkhaki': '#BDB76B',
'darkmagenta': '#8B008B',
'darkolivegreen': '#556B2F',
'darkorange': '#FF8C00',
'darkorchid': '#9932CC',
'darkred': '#8B0000',
'darksalmon': '#E9967A',
'darkseagreen': '#8FBC8F',
'darkslateblue': '#483D8B',
'darkslategray': '#2F4F4F',
'darkslategrey': '#2F4F4F',
'darkturquoise': '#00CED1',
'darkviolet': '#9400D3',
'deeppink': '#FF1493',
'deepskyblue': '#00BFFF',
'dimgray': '#696969',
'dimgrey': '#696969',
'dodgerblue': '#1E90FF',
'firebrick': '#B22222',
'floralwhite': '#FFFAF0',
'forestgreen': '#228B22',
'fuchsia': '#FF00FF',
'gainsboro': '#DCDCDC',
'ghostwhite': '#F8F8FF',
'gold': '#FFD700',
'goldenrod': '#DAA520',
'gray': '#808080',
'green': '#008000',
'greenyellow': '#ADFF2F',
'grey': '#808080',
'honeydew': '#F0FFF0',
'hotpink': '#FF69B4',
'indianred': '#CD5C5C',
'indigo': '#4B0082',
'ivory': '#FFFFF0',
'khaki': '#F0E68C',
'lavender': '#E6E6FA',
'lavenderblush': '#FFF0F5',
'lawngreen': '#7CFC00',
'lemonchiffon': '#FFFACD',
'lightblue': '#ADD8E6',
'lightcoral': '#F08080',
'lightcyan': '#E0FFFF',
'lightgoldenrodyellow': '#FAFAD2',
'lightgray': '#D3D3D3',
'lightgreen': '#90EE90',
'lightgrey': '#D3D3D3',
'lightpink': '#FFB6C1',
'lightsalmon': '#FFA07A',
'lightseagreen': '#20B2AA',
'lightskyblue': '#87CEFA',
'lightslategray': '#778899',
'lightslategrey': '#778899',
'lightsteelblue': '#B0C4DE',
'lightyellow': '#FFFFE0',
'lime': '#00FF00',
'limegreen': '#32CD32',
'linen': '#FAF0E6',
'magenta': '#FF00FF',
'maroon': '#800000',
'mediumaquamarine': '#66CDAA',
'mediumblue': '#0000CD',
'mediumorchid': '#BA55D3',
'mediumpurple': '#9370DB',
'mediumseagreen': '#3CB371',
'mediumslateblue': '#7B68EE',
'mediumspringgreen': '#00FA9A',
'mediumturquoise': '#48D1CC',
'mediumvioletred': '#C71585',
'midnightblue': '#191970',
'mintcream': '#F5FFFA',
'mistyrose': '#FFE4E1',
'moccasin': '#FFE4B5',
'navajowhite': '#FFDEAD',
'navy': '#000080',
'oldlace': '#FDF5E6',
'olive': '#808000',
'olivedrab': '#6B8E23',
'orange': '#FFA500',
'orangered': '#FF4500',
'orchid': '#DA70D6',
'palegoldenrod': '#EEE8AA',
'palegreen': '#98FB98',
'paleturquoise': '#AFEEEE',
'palevioletred': '#DB7093',
'papayawhip': '#FFEFD5',
'peachpuff': '#FFDAB9',
'peru': '#CD853F',
'pink': '#FFC0CB',
'plum': '#DDA0DD',
'powderblue': '#B0E0E6',
'purple': '#800080',
'rebeccapurple': '#663399',
'red': '#FF0000',
'rosybrown': '#BC8F8F',
'royalblue': '#4169E1',
'saddlebrown': '#8B4513',
'salmon': '#FA8072',
'sandybrown': '#F4A460',
'seagreen': '#2E8B57',
'seashell': '#FFF5EE',
'sienna': '#A0522D',
'silver': '#C0C0C0',
'skyblue': '#87CEEB',
'slateblue': '#6A5ACD',
'slategray': '#708090',
'slategrey': '#708090',
'snow': '#FFFAFA',
'springgreen': '#00FF7F',
'steelblue': '#4682B4',
'tan': '#D2B48C',
'teal': '#008080',
'thistle': '#D8BFD8',
'tomato': '#FF6347',
'turquoise': '#40E0D0',
'violet': '#EE82EE',
'wheat': '#F5DEB3',
'white': '#FFFFFF',
'whitesmoke': '#F5F5F5',
'yellow': '#FFFF00',
'yellowgreen': '#9ACD32'}
Durch Setzen des Parameters color im Plot-Befehl kann nun eine Farbe aus einer der oberen Farbpaletten gewählt werden:
x = np.linspace(0,1,10)
plt.plot(x,0.5*x*(1-x),'o-',color='g') # Grundfarbe
plt.plot(x,x*(1-x),'d-',color='tab:olive') # Tableau-Farbe
plt.plot(x,1.5*x*(1-x),'s-',color='firebrick') # CSS-Farbe
plt.show()
Bei der Fehleranalyse sind oft logarithmische Achsen von Interesse. Angenommen, wir analysieren einen iterativen Algorithmus und messen die Entfernung \(err_n\) zwischen exakter Lösung und der berechneten Näherungslösung nach \(n\) Iterationen. Man sagt, das Verfahren konvergiert:
Q-linear, falls \(err_n \leq C, err_{n-1}\) mit \(C \in (0,1)\)
Q-superlinear, falls \(err_n \leq \varepsilon_n, err_{n-1}\) mit einer Nullfolge \(\varepsilon_n \searrow 0\)
Q-quadratisch, falls \(err_n \leq C, err_{n-1}^2\) mit \(C > 0\)
Stellen wir den Fehlerverlauf in einem kartesischen Koordinatensystem und einem Koordinatensystem mit logarithmischer \(y\)-Achse dar:
import math
n = np.array(range(1,6), dtype='float64')
err_p1 = (0.8)**n
err_p2 = [1./math.factorial(int(i)) for i in n]
err_p3 = (0.8)**(2**n)
plt.figure(figsize=(10,5))
def generate_plot():
plt.plot(n, err_p1, 'ro-', label='Q-linear')
plt.plot(n, err_p2, 'bo-', label='Q-superlinear')
plt.plot(n, err_p3, 'co-', label='Q-quadratisch')
plt.grid()
# Plot in kartesischen Koordinatensystem
plt.subplot(1,2,1)
generate_plot()
plt.legend(loc='upper right')
# Plot in Koordinatensystem mit logarithmischer y-Achse
plt.subplot(1,2,2)
generate_plot()
plt.semilogy()
plt.legend(loc='lower left')
plt.show()
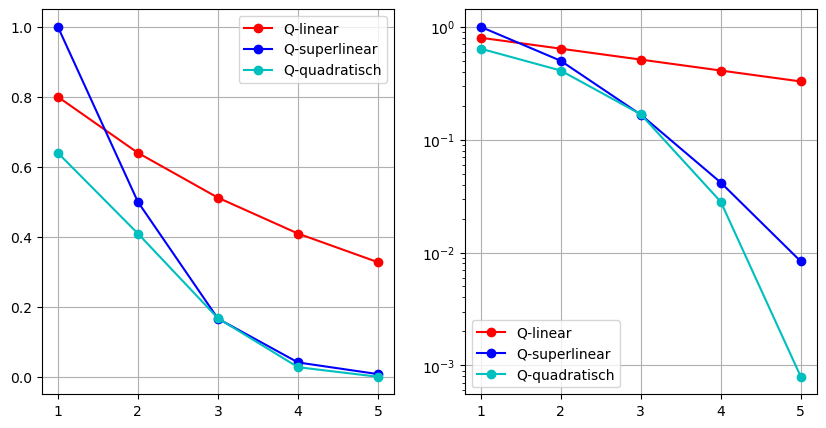
Wir sehen, dass eine \(Q\)-linear konvergente Folge im Plot mit logarithmischer \(y\)-Achse einer lineare Funktion ist.
Analog dazu kann man auch die \(x\)-Achse mit plt.semilogx() logatithmisch skalieren, was bei oben vorgestellter Anwendung allerdings wenig Sinn macht.
Balken-, Linien- und Kuchendiagramme#
Schauen wir uns weitere elementare Plot-Typen an. Angenommen wir haben die Auswertung einer Umfrage vorliegen, und möchten diese graphisch aufbereiten. Unsere Beispieldaten sind:
parties = ["CDU", "SPD", "FDP", "Grüne", "Linke", "AfD", "Sonstige"]
colors = ["black", "red", "yellow", "green", "violet", "blue", "gray"]
values = [25.3, 26.3, 13.9, 14.2, 6.2, 4.9]
values.append(100-sum(values))
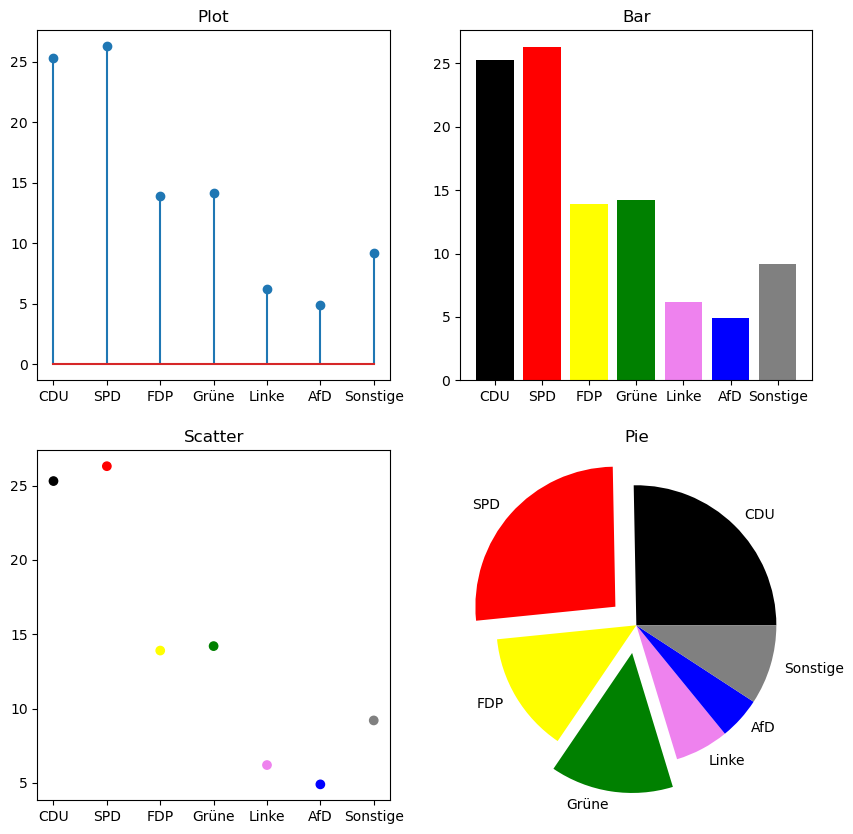
Wir können anstelle des plot-Befehls auch stem verwenden um ein Liniendiagramm zu erstellen, scatter für ein Streudiagramm, bar für ein Balkendiagramm oder pie für ein Tortendiagramm. Im folgenden Beispiel werden die Unterschiede gezeigt:
plt.figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.stem(parties, values)
plt.title("Plot")
plt.subplot(2,2,2)
plt.bar(parties, values, color=colors)
plt.title("Bar")
plt.subplot(2,2,3)
plt.scatter(parties, values, color=colors)
plt.title("Scatter")
plt.subplot(2,2,4)
plt.pie(values, labels=parties, explode=[0,0.2,0,0.2,0,0,0], colors=colors)
plt.title("Pie")
plt.show()
Object-oriented Interface#
Gestaltung von Plots#
Nach dem wir uns nun mit der ersten Ebene befasst haben, befassen wir uns jetzt mit der zweiten Ebene von matplotlib. Dazu benötigen wir oftmals den Befehle ax.plot().
import pandas as pd
Kurs_ALV = pd.read_csv("./../../Data/Allianz_Schlusskurse_2020_2025.csv")
Kurs_ALV=pd.read_csv("./../../Data/Allianz_Schlusskurse_2020_2025.csv", header=1) # To-Do: Anpassen; header = csv beginnt in Spalte eins nicht mit Kurs und Datum, sondern mit Ticker.
Kurs_ALV = Kurs_ALV.rename(columns={"Ticker": "Datum", "ALV.DE": "Schlusskurs"}) #Spaltenbeschriftungen umbennen
Kurs_ALV = Kurs_ALV.drop(0).reset_index(drop=True) #Erste Zeile rauswerfen --> drop(0); Mit .reset_index(drop=True) wird der Index neu durchnummeriert (0, 1, 2, …); Sonst bleibt der alte Index erhalten und wir beginnen mit Index 1
print(Kurs_ALV)
# Datumskonvertierung
Kurs_ALV["Datum"] = pd.to_datetime(Kurs_ALV["Datum"])
# Plot erstellen
plt.figure(figsize=(12,6))
plt.plot(Kurs_ALV["Datum"], Kurs_ALV["Schlusskurs"], label="Allianz Schlusskurs")
# Chart soll gleich an y-Achse starten
plt.xlim(Kurs_ALV["Datum"].min(), Kurs_ALV["Datum"].max())
plt.title("Allianz Schlusskurse (2020–2025)")
plt.xlabel("Datum")
plt.ylabel("Schlusskurs (€)")
plt.grid(True)
plt.show()
Datum Schlusskurs
0 2020-01-02 163.322479
1 2020-01-03 161.515991
2 2020-01-06 160.520554
3 2020-01-07 160.889252
4 2020-01-08 160.962997
... ... ...
1270 2024-12-19 284.622162
1271 2024-12-20 282.417297
1272 2024-12-23 282.033844
1273 2024-12-27 282.896606
1274 2024-12-30 283.663513
[1275 rows x 2 columns]
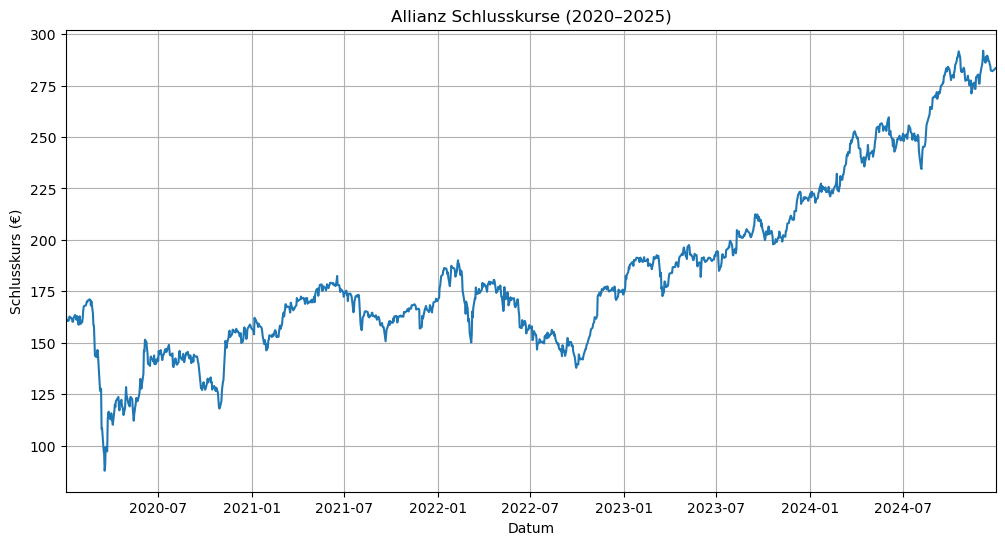
Wir können auch Daten dem Diagramm hinzufügen.
concerns = pd.read_csv("./../../Data/Kurse_ASTBDR.csv", sep=";", decimal=",") # Decimal="," wegen europäischer Schreibweise -> TO-Do: Pfad anpassen
concerns["Datum"] = pd.to_datetime(concerns["Datum"], dayfirst=True) # dayfirst=True = Tag kommt vor dem Monat
# Plot erstellen
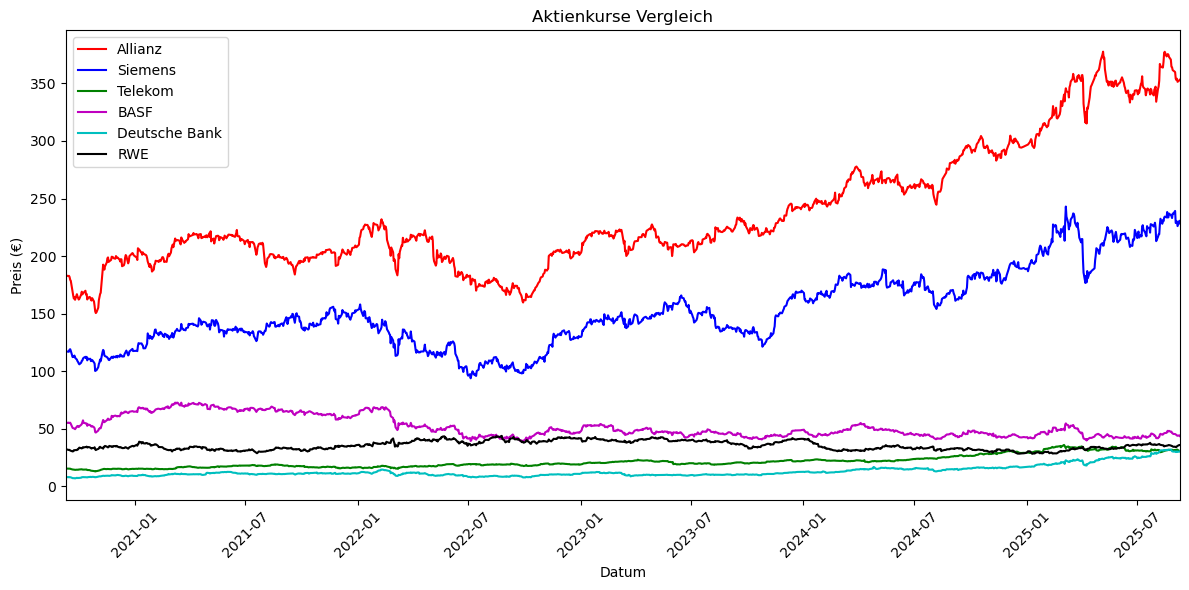
fig, ax = plt.subplots(figsize=(12, 6))
# Einzelne Plots
ax.plot(concerns["Datum"], concerns["Allianz"], label="Allianz", color="r")
ax.plot(concerns["Datum"], concerns["Siemens"], label="Siemens", color="b")
ax.plot(concerns["Datum"], concerns["Telekom"], label="Telekom", color="g")
ax.plot(concerns["Datum"], concerns["BASF"], label="BASF", color="m")
ax.plot(concerns["Datum"], concerns["Deutsche Bank"], label="Deutsche Bank", color="c")
ax.plot(concerns["Datum"], concerns["RWE"], label="RWE", color="k")
plt.xlim(concerns["Datum"].min(), concerns["Datum"].max())
ax.set_xlabel("Datum")
ax.set_ylabel("Preis (€)")
ax.set_title("Aktienkurse Vergleich")
ax.legend()
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()
/tmp/ipykernel_3384082/2366942567.py:3: UserWarning: Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.
concerns["Datum"] = pd.to_datetime(concerns["Datum"], dayfirst=True) # dayfirst=True = Tag kommt vor dem Monat
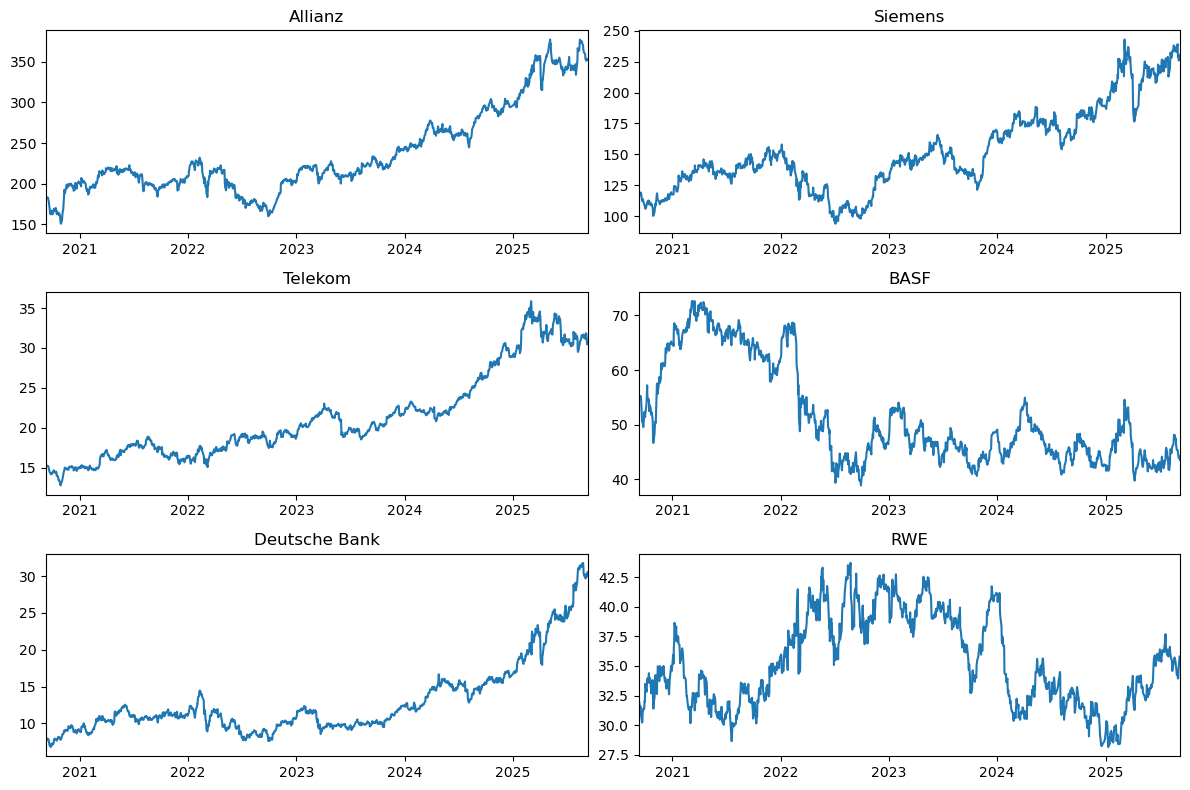
Nachfolgend sehen Sie, wie wir Unterdiagramme erstellen können. In den meisten Fällen benötigen wir für eine feinere Kontrolle das Package matplotlib.dates und verbinden das mit eine for-Schleife. Ein Beispiel dafür finden Sie hier.
import matplotlib.dates as mdates
# Subplots 3x2
fig, ax = plt.subplots(3, 2, figsize=(12, 8), sharex=True)
ax[0, 0].plot(concerns["Datum"], concerns["Allianz"])
ax[0, 0].set_title("Allianz")
ax[0, 1].plot(concerns["Datum"], concerns["Siemens"])
ax[0, 1].set_title("Siemens")
ax[1, 0].plot(concerns["Datum"], concerns["Telekom"])
ax[1, 0].set_title("Telekom")
ax[1, 1].plot(concerns["Datum"], concerns["BASF"])
ax[1, 1].set_title("BASF")
ax[2, 0].plot(concerns["Datum"], concerns["Deutsche Bank"])
ax[2, 0].set_title("Deutsche Bank")
ax[2, 1].plot(concerns["Datum"], concerns["RWE"])
ax[2, 1].set_title("RWE")
plt.xlim(concerns["Datum"].min(), concerns["Datum"].max())
# Jahreszahlen
locator = mdates.YearLocator() # mdates.YearLocator() -> setzt die Tick-Positionen auf Jahresanfänge
formatter = mdates.DateFormatter("%Y") # formatiert die Labels als "2020", "2021", ...
for axes in ax.flat: # gehe über JEDES einzelne Unterdiagramm
axes.xaxis.set_major_locator(locator) # sage der X-Achse: benutze Jahres-Ticks
axes.xaxis.set_major_formatter(formatter) # beschrifte die Ticks nur mit der Jahreszahl
axes.tick_params(labelbottom=True) # # zwinge, dass die Jahreszahlen auch angezeigt werden
plt.tight_layout()
plt.show()
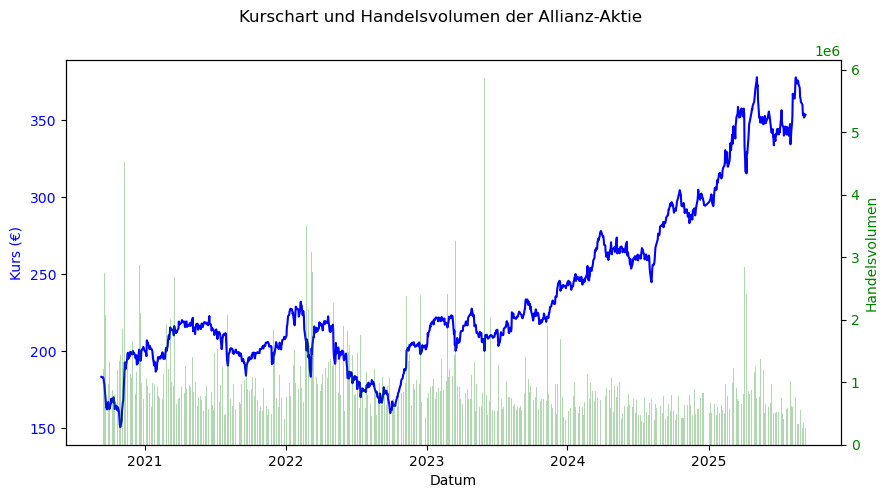
Wir können auch zwei y-Achsen verwenden, wenn wir z.B. den Aktienkurs und das Handelsvolumen in einem Liniendiagramm darstellen wollen.
import numpy as np
alv_vol = pd.read_csv("./../../Data/Allianz_Vol_Price_2020.csv", sep=";", decimal=",") # Decimal="," wegen europäischer Schreibweise -> TO-Do: Pfad anpassen
print(alv_vol)
Schluss=alv_vol["Schluss"]
Volumen=alv_vol["Volumen"]
fig, ax1 = plt.subplots(figsize=(10,5))
# Datumkonvertierung
alv_vol["Datum"] = pd.to_datetime(alv_vol["Datum"], dayfirst=True, errors="coerce")
# Hier müssen jetzt die Zahlen im csv konvertiert werden
alv_vol["Schluss"] = pd.to_numeric(alv_vol["Schluss"], errors="coerce")
alv_vol["Volumen"] = pd.to_numeric(alv_vol["Volumen"], errors="coerce")
# linke y-Achse: Kurs
ax1.plot(alv_vol["Datum"], Schluss, color="b", label="Kurs")
ax1.set_xlabel("Datum")
ax1.set_ylabel("Kurs (€)", color="b")
ax1.tick_params(axis="y", labelcolor="b")
# rechte y-Achse: Volumen
ax2 = ax1.twinx() # wir teilen ja für beide y-Achsen die x-Achse
ax2.bar(alv_vol["Datum"], Volumen, color="green", alpha=0.3, label="Volumen")
ax2.set_ylabel("Handelsvolumen", color="green")
ax2.tick_params(axis="y", labelcolor="green")
fig.suptitle("Kurschart und Handelsvolumen der Allianz-Aktie")
plt.show()
Datum Schluss Volumen
0 10.09.20 183.16 717596
1 11.09.20 183.02 869256
2 14.09.20 182.58 579184
3 15.09.20 182.80 743918
4 16.09.20 181.80 1204644
... ... ... ...
1270 03.09.25 353.00 495000
1271 04.09.25 354.10 341216
1272 05.09.25 351.40 398283
1273 08.09.25 352.70 274437
1274 09.09.25 353.30 269502
[1275 rows x 3 columns]
/tmp/ipykernel_3384082/2819810138.py:11: UserWarning: Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.
alv_vol["Datum"] = pd.to_datetime(alv_vol["Datum"], dayfirst=True, errors="coerce")
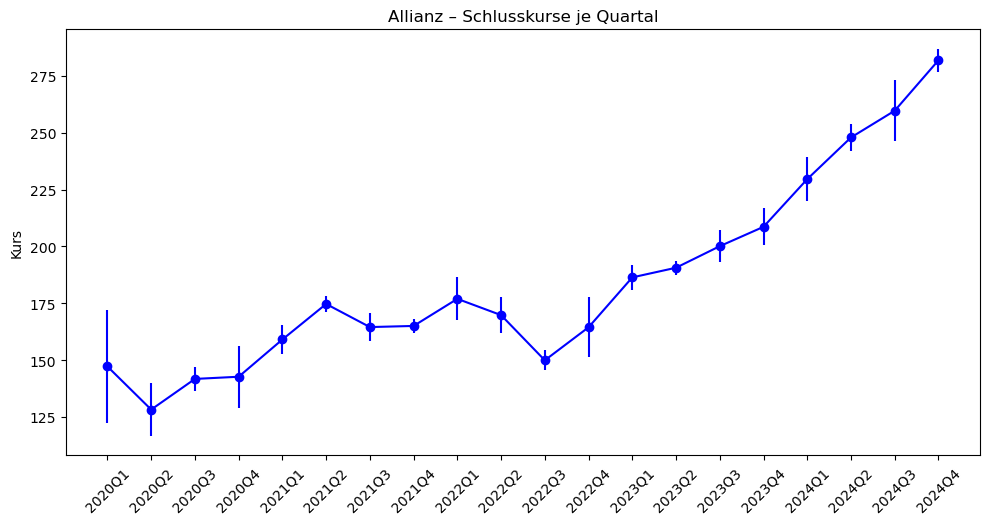
Error-Bars#
Eine angenehme Methode für Visualisierungen ist der Error-Bar, da dieser grafisch die Standardabweichung zu einem bestimmten (Zeit-)Punkt darstellt. Der nachfolgende Code mit ax.errorbar() demonstriert die einmal.
Für die Datumskonvertierung finden Sie unter den nachfolgenden Verlinkungen Hilfe 1, 2 und 3.
### Datum konvertieren
Kurs_ALV["Datum"] = pd.to_datetime(Kurs_ALV["Datum"], errors="coerce") # errors="coerce": ersetzt ungültige Werte durch NaT (bei Datumswerten) bzw. NaN (bei Zahlen); mithilfe von errors=coerce" gehen wir sicher, dass alle Werte in der Spalte in ein Datumformat konvertiert worden sind. Alternativ errors=ignore oder errors=raise
# Quartale bilden und aggregieren
Kurs_ALV["Quartal"] = Kurs_ALV["Datum"].dt.to_period("1Q")
gruppen = Kurs_ALV.groupby("Quartal")["Schlusskurs"]
mittel = gruppen.mean()
std = gruppen.std()
## Erstellung error-bar
fig, ax = plt.subplots(figsize=(10,5)) # Diagramm vergrößern (Breite=10 Zoll, Höhe=5 Zoll)
ax.errorbar(
mittel.index.astype(str), # Achtung, wir haben mit mittel.index keine Zahl o.ä. Matplotlib kann PeriodIndex nicht direkt verarbeiten, da wir Jahr+Quartal haben (Benutzerdefiniert). Wir müssen hier als den Index in einen String umwandeln.
mittel.values,
yerr=std.values,
marker="o",
linestyle="-",
color="b",
)
ax.set_title("Allianz – Schlusskurse je Quartal")
ax.set_ylabel("Kurs")
plt.tight_layout() # Passt das Layou des Diagramms automatisch an.
plt.xticks(rotation=45)
plt.show()
Boxplots#
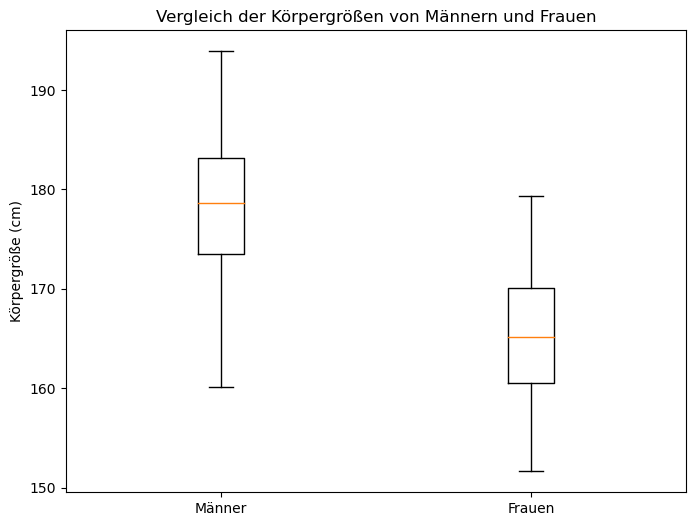
Ein Boxplot ist ein Diagramm zur Darstellung der Verteilung von Daten. Er zeigt den Median, das untere (Q1) und obere Quartil (Q3), den Interquartilsabstand (IQR) sowie die Whiskers. Werte außerhalb dieses Bereichs werden als Ausreißer markiert. Mithilfe von ax.boxplot() können wir ganz einfach einen Boxplot erzeugen.
np.random.seed(0) # gleiche „zufällige“ Zahlen bei jedem Lauf
maenner = np.random.normal(loc=178, scale=7, size=100) # Männer: Mittelwert 178 cm, Streuung 12
frauen = np.random.normal(loc=165, scale=6, size=100) # Frauen: Mittelwert 165 cm, Streuung 8
df = pd.DataFrame({
"Männer": maenner,
"Frauen": frauen
})
# Boxplot erstellen
fig, ax = plt.subplots(figsize=(8,6))
ax.boxplot([df["Männer"], df["Frauen"]],
labels=["Männer", "Frauen"])
ax.set_title("Vergleich der Körpergrößen von Männern und Frauen")
ax.set_ylabel("Körpergröße (cm)")
plt.show()
Weitere Grafiken mit Matplotlib#
Erstellung der Farbpalette#
Dieser Python-Code verwendet die Bibliotheken matplotlib.pyplot und matplotlib.colors, um eine übersichtliche Visualisierung verschiedener Farbpaletten in Tabellenform zu erstellen. Mit Hilfe einer zentralen Funktion namens plot_colortable werden Farbnamen und ihre entsprechenden Farbfelder grafisch dargestellt. Der Code zeigt dabei exemplarisch drei verschiedene Farbsets: die Grundfarben (BASE_COLORS), die Tableau-Palette (TABLEAU_COLORS) sowie die CSS4-Farben (CSS4_COLORS), die allesamt vordefinierte Farbnamen aus Matplotlibs Farbsystem sind. Optional ließe sich auch die sehr umfangreiche XKCD-Farbsammlung darstellen, was allerdings eine sehr große Grafik erzeugen würde.
Praktisch ist dieser Code besonders nützlich, wenn man sich einen schnellen Überblick über verfügbare Farben und deren Namen verschaffen möchten – etwa bei der Auswahl konsistenter Farben für Diagramme, Benutzeroberflächen oder Präsentationen. Die Farben können alphabetisch oder nach Farbwerten sortiert angezeigt werden, was eine einfache Orientierung innerhalb großer Farbsammlungen ermöglicht.
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
def plot_colortable(colors, title, sort_colors=True, emptycols=0):
cell_width = 212
cell_height = 22
swatch_width = 48
margin = 12
topmargin = 40
# Sort colors by hue, saturation, value and name.
if sort_colors is True:
by_hsv = sorted((tuple(mcolors.rgb_to_hsv(mcolors.to_rgb(color))),
name)
for name, color in colors.items())
names = [name for hsv, name in by_hsv]
else:
names = list(colors)
n = len(names)
ncols = 4 - emptycols
nrows = n // ncols + int(n % ncols > 0)
width = cell_width * 4 + 2 * margin
height = cell_height * nrows + margin + topmargin
dpi = 72
fig, ax = plt.subplots(figsize=(width / dpi, height / dpi), dpi=dpi)
fig.subplots_adjust(margin/width, margin/height,
(width-margin)/width, (height-topmargin)/height)
ax.set_xlim(0, cell_width * 4)
ax.set_ylim(cell_height * (nrows-0.5), -cell_height/2.)
ax.yaxis.set_visible(False)
ax.xaxis.set_visible(False)
ax.set_axis_off()
ax.set_title(title, fontsize=24, loc="left", pad=10)
for i, name in enumerate(names):
row = i % nrows
col = i // nrows
y = row * cell_height
swatch_start_x = cell_width * col
text_pos_x = cell_width * col + swatch_width + 7
ax.text(text_pos_x, y, name, fontsize=14,
horizontalalignment='left',
verticalalignment='center')
ax.add_patch(
Rectangle(xy=(swatch_start_x, y-9), width=swatch_width,
height=18, facecolor=colors[name], edgecolor='0.7')
)
return fig
plot_colortable(mcolors.BASE_COLORS, "Grundfarben",
sort_colors=False, emptycols=1)
plot_colortable(mcolors.TABLEAU_COLORS, "Tableau-Palette",
sort_colors=False, emptycols=2)
plot_colortable(mcolors.CSS4_COLORS, "CSS-Farben")
# Optionally plot the XKCD colors (Caution: will produce large figure)
# xkcd_fig = plot_colortable(mcolors.XKCD_COLORS, "XKCD Colors")
# xkcd_fig.savefig("XKCD_Colors.png")
plt.show()



Plots für Skalar- und Vektorfelder#
Auch für die graphische Darstellung von Skalarfeldern \(f\colon \mathbb{R}^2 \to \mathbb{R}\) und Vektorfeldern \(\vec F\colon \mathbb{R}^2 \to \mathbb{R}^2\) stehen einige Funktionen in Matplotlib bereit. Die meisten Funktionen zur Darstellung von Skalarfeldern erwarten als Argument 3 Matrizen, eine für die \(x\)-Koordinaten, eine für die \(y\)-Koordinaten und eine für den Funktionswert \(f(x,y)\). Hilfreich ist hier die Funktion numpy.meshgrid mit der wir ein 2D-Tensorprodukt-Gitter aus 2 1D-Gittern erzeugen:
# 1D-Gitter für x- und y-Variable
x = np.linspace(-4.5,3.5,1001)
y = np.linspace(-3.5,3.5,1001)
# 2D-Gitter erzeugen
X,Y = np.meshgrid(x,y)
# Definiere Himmelblau-Funktion
Z = (X**2 + y - 11)**2 + (X + Y**2 - 7)**2
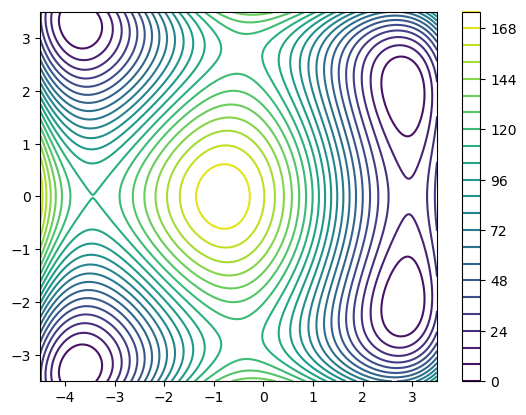
Eine mögliche Darstellung einer solchen Funktion wäre ein Contour-Plot, in welchem die Kurven \(\{(x,y)\colon f(x,y)=c_i\}\) für verschiedene Werte \(c_1<c_2 < \ldots<c_{\text{levels}}\) eingezeichnet werden:
plt.contour(X,Y,Z, levels=25)
plt.colorbar()
plt.show()
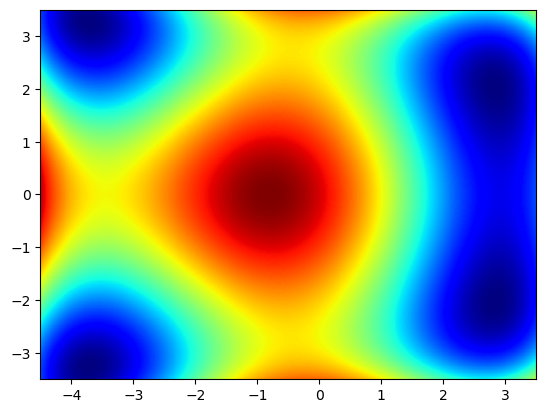
Ähnlich funktionieren Color-Plots, bei denen der Funktionswert an einer Stelle \((x,y)\) dem Farbwert einer vordefinierten Farbpalette entspricht:
import matplotlib.cm as cm
plt.pcolormesh(X,Y,Z, cmap=cm.jet)
plt.show()
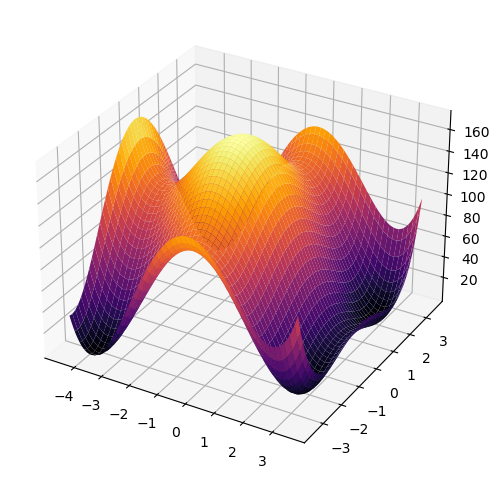
Skalarfelder lassen sich auch in dreidimensionalen Koordinatensystemen darstellen. Die Argumente werden auf \(x\)- und \(y\)-Achse aufgetragen, und der Funktionswert auf die \(z\)-Achse. Die entsprechenden Plot-Befehle sind allerdings nicht im Submodul matplotlib.pyplot definiert, daher müssen wir einen Umweg nehmen. Zunächst erzeugen wir uns ein Bildobjekt mit
fig = plt.figure()
fügen ein 3D-Koordinatensystem hinzu
ax = fig.axes(projection='3d')
und nutzen die vom Objekt ax bereitgestellten Plot-Befehle. Hier ein Beispiel:
plt.figure(figsize=(8,6))
# 3D-Koordinatensystem hinzufügen
ax = plt.axes(projection='3d')
# Surface-Plot erstellen
ax.plot_surface(X,Y,Z, cmap=cm.inferno)
plt.show()
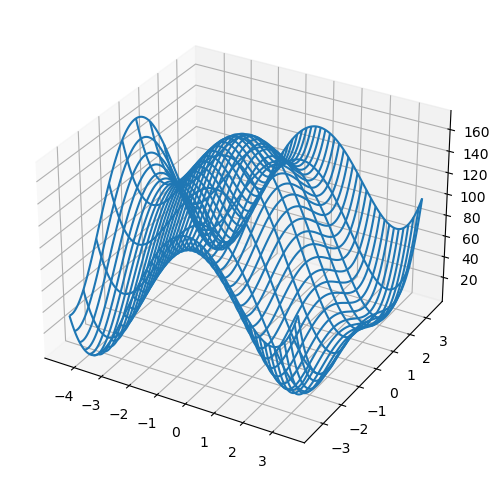
plt.figure(figsize=(8,6))
ax = plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z, rcount=10)
plt.show()
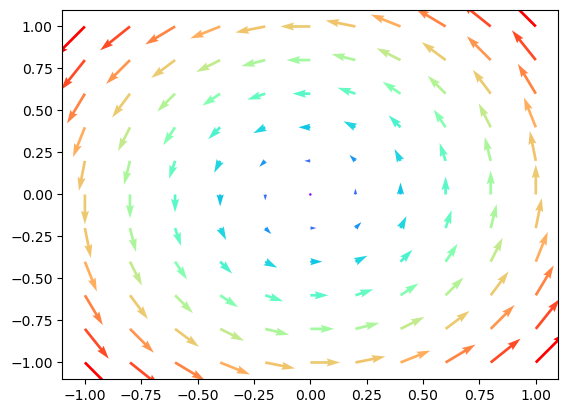
Schauen wir uns noch eine Methode mit der wir Vektorfelder zeichnen können. Als Beispiel definieren wir \(\vec f(x,y) = (-y,x)^\top\). Solche Vektorfelder können in sogenannten Quiver-Plots dargestellt werden:
x = np.linspace(-1,1, 11)
y = np.linspace(-1,1, 11)
# Punktgitter definieren
X,Y = np.meshgrid(x, y)
# Funktionswerte von F
Z1 = -Y
Z2 = X
# Optional: Färbe Pfeile nach Länge
C = np.sqrt(Z1**2 + Z2**2)
# Quiverplot erzeugen und anzeigen
plt.quiver(X, Y, Z1, Z2, C, cmap=cm.rainbow)
plt.show()
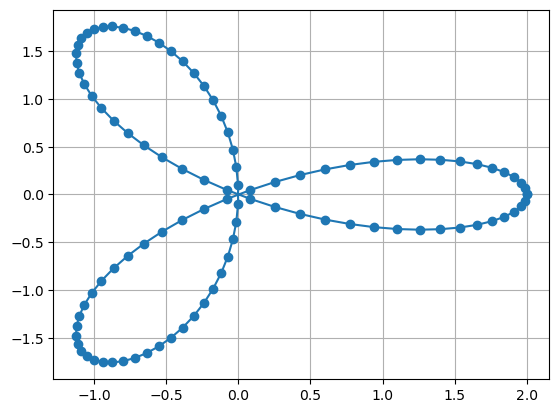
Auch Kurven lassen sich in Matplotlib zeichnen. Eine Kurve ist zunächst eine Menge an Punkten
mit einer sogenannten Kurvenparametrisierung \(\vec x\colon[t_a,t_b]\to\mathbb{R}^n\), welche regulär ist, d.h., \(\dot{\vec x}(t)\ne 0\) für alle \(t\in [t_a,t_b]\). Für eine ebene Kurve (\(n=2\)) können wir den normalen Plot-Befehl nutzen. Das Kleeblatt
zeichnen wir beispielsweise mit
t = np.linspace(0,2*np.pi,100)
x = np.cos(t)+np.cos(2*t)
y = np.sin(t)-np.sin(2*t)
plt.plot(x,y,'o-')
plt.grid()
plt.show()
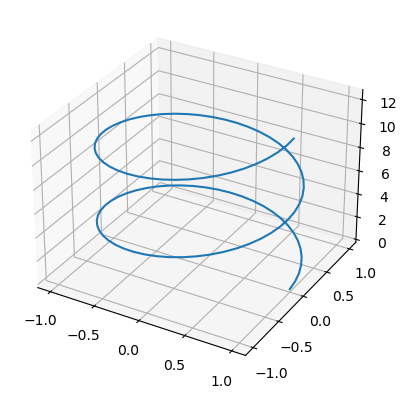
Ähnlich kann man Raumkurven (\(n=3\)) zeichnen, man benötigt nur vorher ein dreidimensionales Koordinatensystem. Wie wir das anlegen haben wir aber schon gesehen. Wir zeichnen hier die Schraubenlinie
t = np.linspace(0,4*np.pi,100)
x = np.cos(t)
y = np.sin(t)
z = t
ax = plt.axes(projection='3d')
ax.plot3D(x, y, z)
plt.show()
Visualisierungen mit Seaborn#
Fassen wir kurz zusammen, matplotlib.pyplot setzt seinen Schwerpunkt auf low-level plotting und volle Kontrolle, verbunden jedoch mit viel Handarbeit. Pandas hingegen ist besonders bequem, wenn man schnelle Diagramme aus DataFrames erzeugen will und bringt den Vorteil mit sich, dass wir Daten importieren können.
Seaborn legt den Fokus auf einen einfachen Syntax und anschaulichen Plot-Design. Mit diesem Package wollen wir uns nachfolgend intensiver befassen. Hier finden Sie weitere Informationen zu Seaborn.
Zu erst installieren wir das Package über unsere Konsole bzw. Terminal.
conda install -c conda-forge seaborn
In Python verwenden wir folgenden Code, um das Seaborn aktiv nutzen zu können.
import seaborn as sns
Übrigens die Abkürzung sns kommt von dem Fernsehcharakter Samuel Norman Seaborn aus der US-TV-Serie The West Wing.
Zähldiagramme#
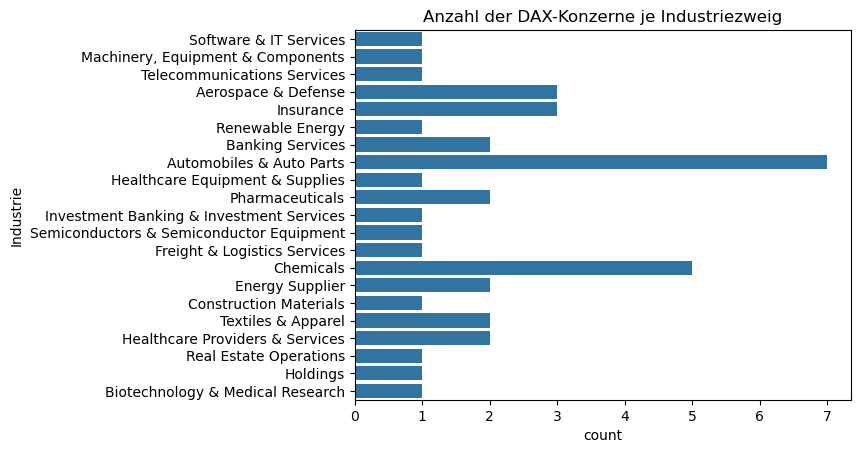
Das nachstehende Codebeispiel demonstriert die Implementierung eines Zähldiagramms mithilfe von sns.countplot() zur Analyse kategorialer Merkmalsausprägungen.
import seaborn as sns
DAX_40=pd.read_csv("./../../Data/DAX40_Daten.csv", sep=";", header=1)
print(DAX_40["Industrie"])
sns.countplot(DAX_40["Industrie"])
plt.title("Anzahl der DAX-Konzerne je Industriezweig")
plt.show()
0 Software & IT Services
1 Machinery, Equipment & Components
2 Telecommunications Services
3 Aerospace & Defense
4 Insurance
5 Aerospace & Defense
6 Renewable Energy
7 Insurance
8 Banking Services
9 Automobiles & Auto Parts
10 Healthcare Equipment & Supplies
11 Automobiles & Auto Parts
12 Automobiles & Auto Parts
13 Pharmaceuticals
14 Investment Banking & Investment Services
15 Semiconductors & Semiconductor Equipment
16 Freight & Logistics Services
17 Automobiles & Auto Parts
18 Chemicals
19 Energy Supplier
20 Banking Services
21 Construction Materials
22 Automobiles & Auto Parts
23 Insurance
24 Textiles & Apparel
25 Chemicals
26 Pharmaceuticals
27 Healthcare Providers & Services
28 Energy Supplier
29 Real Estate Operations
30 Chemicals
31 Aerospace & Defense
32 Automobiles & Auto Parts
33 Healthcare Providers & Services
34 Holdings
35 Chemicals
36 Automobiles & Auto Parts
37 Biotechnology & Medical Research
38 Chemicals
39 Textiles & Apparel
Name: Industrie, dtype: object
Histograme#
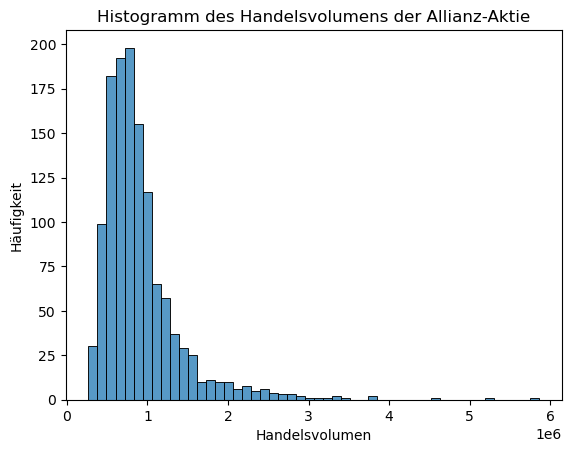
Ein Histogramm mit überlagerter Dichtefunktion bietet eine anschauliche Möglichkeit, die Verteilung der Messwerte zu untersuchen. Dazu nutzen wir sns.histplot().
sns.histplot(alv_vol["Volumen"], bins=50)
plt.xlabel("Handelsvolumen")
plt.ylabel("Häufigkeit")
plt.title("Histogramm des Handelsvolumens der Allianz-Aktie")
plt.show()
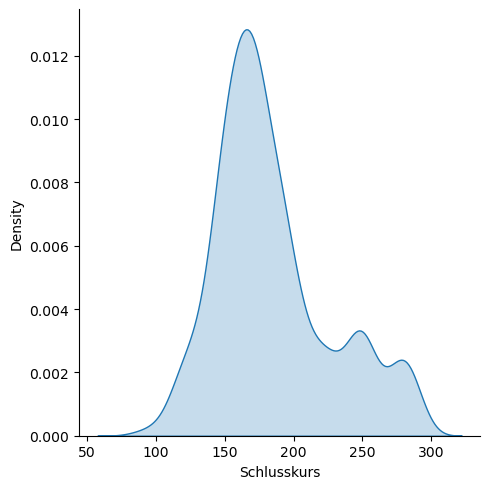
Wenn wir nur die Dichtefunktion uns ausgeben wollen, dann können wir das mithilfe von sns.displot ganz einfach erzeugen.
sns.displot(Kurs_ALV["Schlusskurs"], kind="kde", fill=True)
/HOME1/users/personal/dana/miniconda3/envs/finance/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
<seaborn.axisgrid.FacetGrid at 0x7f0f9f8659d0>
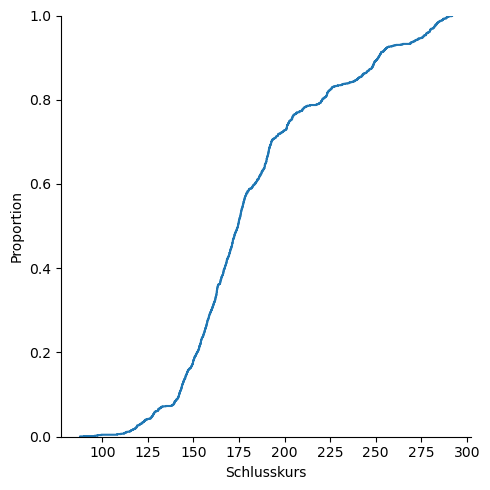
Der nachfolgende Code zeigt uns, wie wir die Verteilungsfunktion ausgeben lassen.
sns.displot(Kurs_ALV["Schlusskurs"], kind="ecdf")
/HOME1/users/personal/dana/miniconda3/envs/finance/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
<seaborn.axisgrid.FacetGrid at 0x7f0fb0378750>
Liniendiagramm#
Im nächsten Programm sehen wir, wie mit seaborn und sns.lineplot ein einfaches Liniendiagramm erstellt werden kann.
print(concerns)
plt.figure()
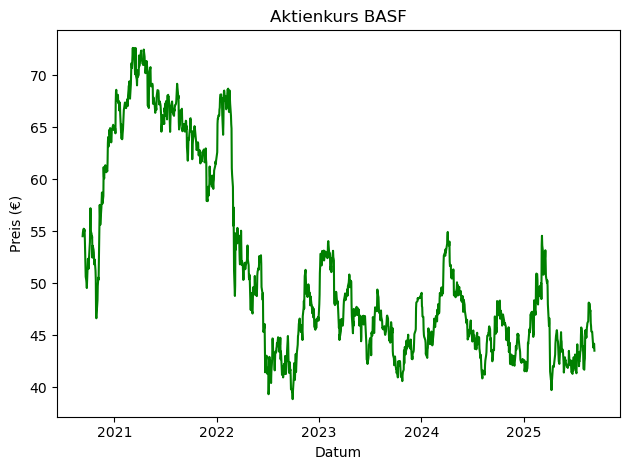
sns.lineplot(data=concerns, x="Datum", y="BASF", color="green")
plt.title("Aktienkurs BASF")
plt.xlabel("Datum")
plt.ylabel("Preis (€)")
plt.tight_layout()
plt.show()
Datum Allianz Siemens Telekom BASF Deutsche Bank RWE
0 2020-09-10 183.16 117.62 15.355 54.51 7.995 32.16
1 2020-09-11 183.02 117.16 15.300 54.87 7.812 32.00
2 2020-09-14 182.58 116.84 15.245 55.23 7.901 31.49
3 2020-09-15 182.80 116.90 15.250 54.91 7.712 31.43
4 2020-09-16 181.80 118.68 15.230 55.06 7.866 31.56
... ... ... ... ... ... ... ...
1270 2025-09-03 353.00 229.45 31.110 44.63 29.800 33.98
1271 2025-09-04 354.10 230.05 31.840 44.00 30.260 34.66
1272 2025-09-05 351.40 226.00 31.650 43.81 29.870 35.02
1273 2025-09-08 352.70 230.65 30.450 44.18 30.030 35.82
1274 2025-09-09 353.30 228.50 30.610 43.51 30.535 35.71
[1275 rows x 7 columns]
Seaborn basiert auf der Philosophie von tidy-Format, das heißt: Jede Beobachtung = 1 Zeile, jede Variable = 1 Spalte. Wir müssen somit unseren Dataframe in ein Long-Format bringen. Dafür verwenden wir den .melt() Befehl. Einige Informationen dazu finden Sie hier. Nach dem .melt() Befehl sieht unser Dataframe in etwa wie folgt aus:
Datum |
Aktie |
Preis |
|---|---|---|
01.01.2020 |
Allianz |
200 |
02.01.2020 |
Allianz |
201 |
01.01.2020 |
Siemens |
120 |
02.01.2020 |
Siemens |
121 |
01.01.2020 |
Telekom |
15 |
02.01.2020 |
Telekom |
16 |
… |
… |
… |
01.01.2025 |
RWE |
35 |
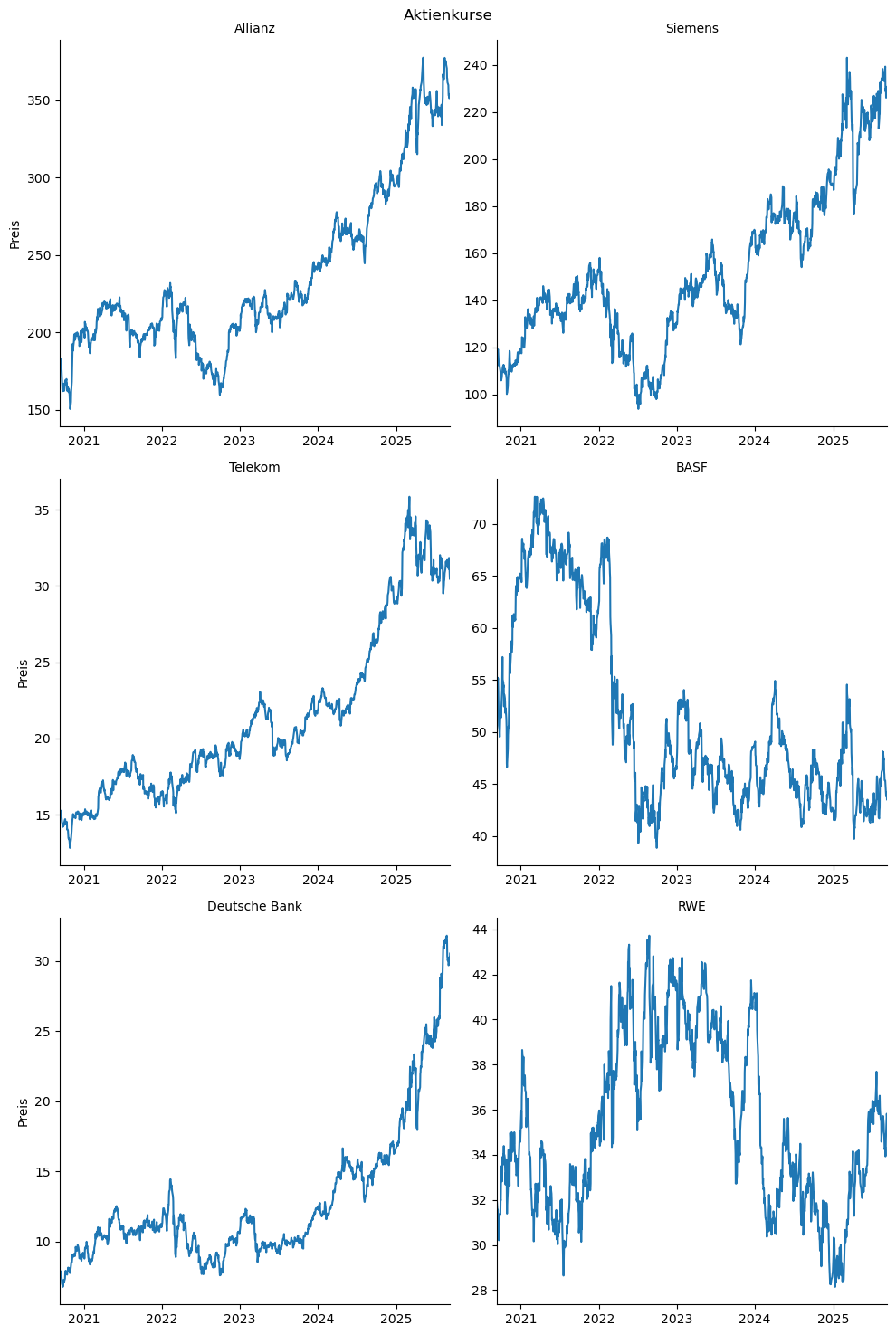
Mithilfe von sns.relplot() geben wir uns Unterdiagramme aus.
cols = ["Allianz", "Siemens", "Telekom", "BASF", "Deutsche Bank", "RWE"]
concerns_long = concerns[["Datum"] + cols].melt(
id_vars="Datum", # Spalte, die fix bleibt
var_name="Aktie", # neue Spalte für die alten Spaltennamen
value_name="Preis" # neue Spalte für die Werte
)
# 3x2-Unterdiagramme (Facets)
g = sns.relplot(
data=concerns_long,
x="Datum", y="Preis",
col="Aktie", col_wrap=2,
kind="line",
facet_kws={"sharex": True, "sharey": False} #eigene y-Achse pro Aktie
)
g.set_titles("{col_name}")
locator = mdates.YearLocator()
formatter = mdates.DateFormatter("%Y")
for ax in g.axes.flat:
ax.xaxis.set_major_locator(locator)
ax.xaxis.set_major_formatter(formatter)
for ax in g.axes.flat:
ax.tick_params(labelbottom=True)
ax.set_xlabel("")
plt.xlim(concerns["Datum"].min(), concerns["Datum"].max())
g.fig.suptitle("Aktienkurse")
plt.tight_layout()
plt.show()
/HOME1/users/personal/dana/miniconda3/envs/finance/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
/tmp/ipykernel_3384082/4153462330.py:32: UserWarning: The figure layout has changed to tight
plt.tight_layout()
Balkendiagramme#
Der nachfolgende Code stellt dar, wie man mit seaborn ein Balkendiagramm erzeugt. Dazu müssen wir matplot.ticker verwenden, um die x-Achse in einer bestimmten Schrittweise darstellen zu können. Eine Übersicht zu den Befehlen finden Sie hier.
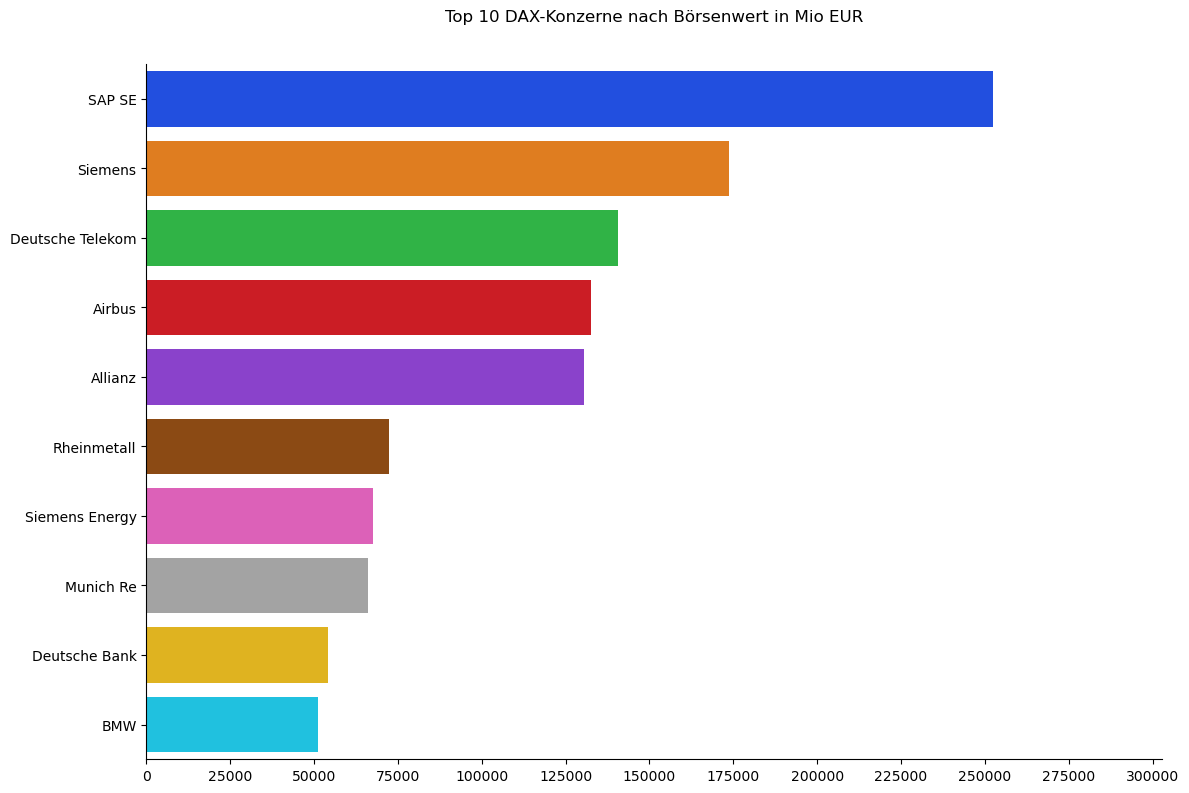
Mit dem sns.barplot() Kommando erstellen wir das Balkendiagramm.
import matplotlib.ticker as ticker
DAX_40 = pd.read_csv(
"./../../Data/DAX40_Daten.csv",
sep=";",
header=1,
decimal=",", # Komma als Dezimaltrennzeichen
thousands="." # Punkt als Tausendertrennzeichen
)
# Kürzere Namen --> Kürzel definieren
Konzern = {
"Allianz SE": "Allianz",
"BASF SE": "BASF",
"Siemens Aktiengesellschaft": "Siemens",
"Deutsche Bank Aktiengesellschaft": "Deutsche Bank",
"Airbus SE": "Airbus",
"Rheinmetall Aktiengesellschaft": "Rheinmetall",
"Siemens Energy AG": "Siemens Energy",
"Münchener Rückversicherungs-Gesellschaft Aktiengesellschaft in München": "Munich Re",
"Bayerische Motoren Werke Aktiengesellschaft": "BMW",
"Deutsche Telekom AG": "Deutsche Telekom",
}
DAX_40["Konzern"] = DAX_40["Unternehmen"].replace(Konzern)
# Top 10 Börsenwerte anzeigen lassen
top10 = DAX_40.sort_values("Börsenwert (Mio EUR)", ascending=False).head(10)
print(top10[["Konzern", "Börsenwert (Mio EUR)"]])
# Plot
plt.figure(figsize=(12,8))
sns.barplot(
data=top10,
x="Börsenwert (Mio EUR)",
y="Konzern",
order=top10["Konzern"],
palette="bright",
hue="Konzern",
legend=False,
orient="h" # Horizontales Balkendiagramm
)
# Rahmen rechts entfernen
sns.despine(left=False, right=True, bottom=False)
plt.title("Top 10 DAX-Konzerne nach Börsenwert in Mio EUR", y=1.05) # Abstand zwischen obersten Balken und Titel
plt.xlabel("")
plt.ylabel("")
# Achsenbegrenzung --> nehme den maximalen Börsenwert und gebe einen Puffer von 10% zum Ende hinzu
max_wert = top10["Börsenwert (Mio EUR)"].max()
plt.xlim(0, max_wert * 1.2)
# X-Achse in 25000er-Schrittenon
plt.gca().xaxis.set_major_locator(ticker.MultipleLocator(25000)) #plt.gca=plot get current axis --> Zugriff direkt auf x-Achse
plt.tight_layout()
plt.show()
Konzern Börsenwert (Mio EUR)
0 SAP SE 252460.2
1 Siemens 173740.9
2 Deutsche Telekom 140764.9
3 Airbus 132564.5
4 Allianz 130417.2
5 Rheinmetall 72432.3
6 Siemens Energy 67525.3
7 Munich Re 66037.6
8 Deutsche Bank 54117.2
9 BMW 51217.5
Regression mit Seaborn#
Mithilfe des seaborn-Packages können ganz schnell und einfach Regressionsplots erstellt werden. Mit sns.regplot() zeichnen wir einen Scatterplot zweier Variablen und passt standardmäßig eine lineare Regressionsgerade mit Konfidenzintervall an die Daten an.
sns.regplot(data=concerns, x=concerns["Allianz"], y=concerns["Deutsche Bank"], marker="+")
<Axes: xlabel='Allianz', ylabel='Deutsche Bank'>
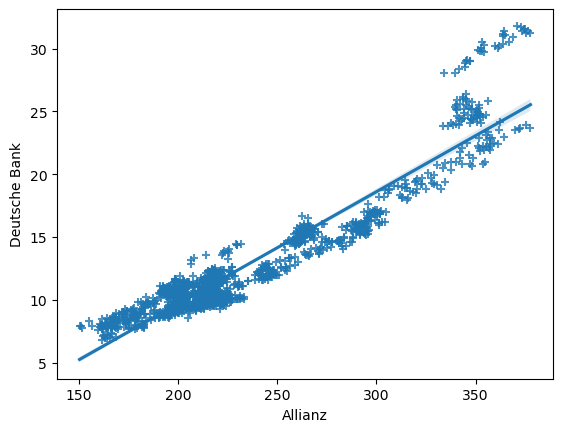
Wenn wir in sns.regplot() den Parameter x_bins verwenden, wird ein Scatterplot erstellt und die vielen Punkte durch fünf Durchschnittspunkte ersetzt werden, sowie eine lineare Regressionsgerade mit Konfidenzintervall eingezeichnet. Diesen Analyse-Trick können wir u.a. verwenden, wenn die Rohdaten als Punktwolke schwer lesbar oder wenig aussagekräftig sind.
sns.regplot(data=concerns, x=concerns["Allianz"], y=concerns["Deutsche Bank"], x_bins=5) # Die x-Achse wird in 5 Intervalle aufgeteilt, und für jedes Intervall wird ein repräsentativer Punkt gezeichnet
<Axes: xlabel='Allianz', ylabel='Deutsche Bank'>
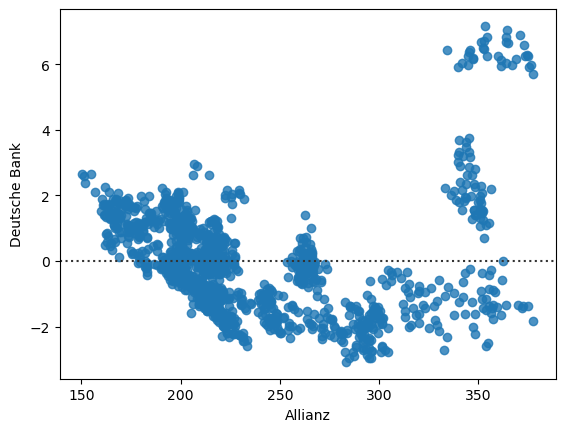
Mit sns.residplot() erstellt mit Seaborn einen Residuenplot: Zunächst wird eine lineare Regression zwischen den Werten der x- und y-Achse berechnet. Anschließend werden die Residuen (also die Abweichungen der beobachteten Werte von den durch die Regressionsgerade vorhergesagten Werten) gegen die x-Achse (in dem Fall Allianz-Werte) aufgetragen. Das Diagramm zeigt damit, ob die lineare Regression die Daten gut beschreibt oder ob systematische Muster in den Abweichungen erkennbar sind.
sns.residplot(data=concerns, x=concerns["Allianz"], y=concerns["Deutsche Bank"])
<Axes: xlabel='Allianz', ylabel='Deutsche Bank'>
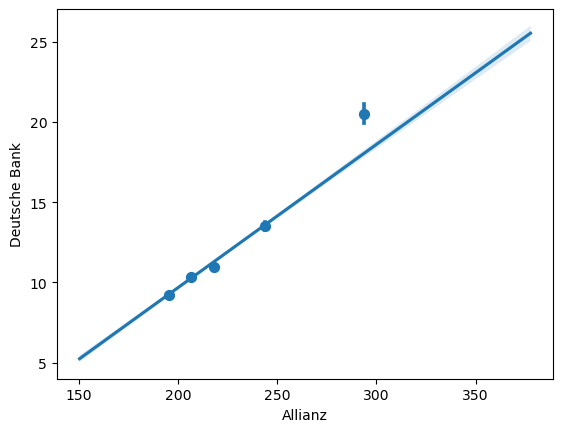
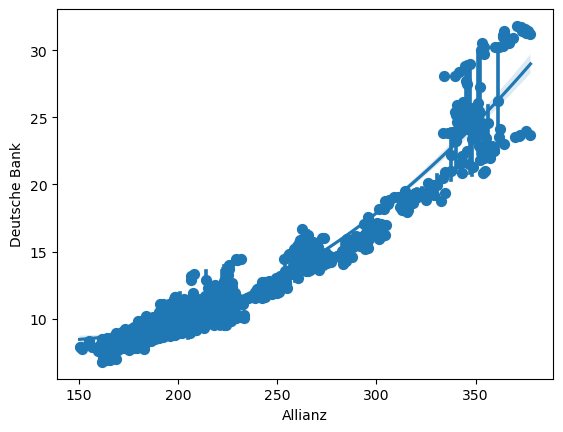
Wir können auch polynomielle Regression anzeigen lassen, in dem wir in den Parameter order nutzen und mit x_estimator=np.mean steuern, welchen Wert seaborn berechnen soll. In dem nachfolgenden Code wäre dies die der Durchschnitt.
sns.regplot(data=concerns, x=concerns["Allianz"], y=concerns["Deutsche Bank"], x_estimator=np.mean, order=2)
<Axes: xlabel='Allianz', ylabel='Deutsche Bank'>
Heatmaps mit Seaborn#
Eine Heatmap ist eine Form der Datenvisualisierung, die Informationen in einer Matrix darstellt und dabei Farben verwendet, um Werte zu kodieren. Jede Zelle der Matrix repräsentiert die Kombination zweier Merkmale, beispielsweise Monate und Wochentage, und die Farbe zeigt die Ausprägung oder Intensität des zugrunde liegenden Wertes an – etwa Häufigkeiten, Durchschnittswerte oder Korrelationen. Der zentrale Nutzen einer Heatmap liegt darin, Muster, Zusammenhänge und Ausreißer schnell erkennbar zu machen, ohne dass Zahlenkolonnen gelesen werden müssen. Besonders in großen Tabellen ermöglicht die farbliche Darstellung, Trends oder Konzentrationen visuell hervorzuheben, die in reinen Zahlen leicht übersehen würden. Heatmaps werden deshalb häufig in der explorativen Datenanalyse, bei Zeitreihen (z. B. Temperaturverläufe) oder in der Korrelationsanalyse eingesetzt, da sie komplexe Strukturen auf eine intuitive und anschauliche Weise vermitteln.
Seaborn ist in der Lage mit einfacher Codierung eine Heatmap zu erstellen. Dafür muss aber im Vorfeld mithilfe von pd.crosstab() ein Grid erstellt werden. Anschließend können wir mit sns.heatmap() uns die Heatmap ausgeben lassen.
temperature=pd.read_csv("./../../Data/bike_share.csv")
print(temperature)
pd.crosstab(temperature["mnth"], temperature["weekday"], values=temperature["temp"], aggfunc="mean")
sns.heatmap(pd.crosstab(temperature["mnth"], temperature["weekday"], values=temperature["temp"], aggfunc="mean"))
dteday season yr mnth holiday weekday workingday weathersit \
0 2011-01-01 1 0 1 0 6 0 2
1 2011-01-02 1 0 1 0 0 0 2
2 2011-01-03 1 0 1 0 1 1 1
3 2011-01-04 1 0 1 0 2 1 1
4 2011-01-05 1 0 1 0 3 1 1
.. ... ... .. ... ... ... ... ...
726 2012-12-27 1 1 12 0 4 1 2
727 2012-12-28 1 1 12 0 5 1 2
728 2012-12-29 1 1 12 0 6 0 2
729 2012-12-30 1 1 12 0 0 0 1
730 2012-12-31 1 1 12 0 1 1 2
temp atemp hum windspeed casual registered \
0 0.344167 0.363625 0.805833 0.160446 331 654
1 0.363478 0.353739 0.696087 0.248539 131 670
2 0.196364 0.189405 0.437273 0.248309 120 1229
3 0.200000 0.212122 0.590435 0.160296 108 1454
4 0.226957 0.229270 0.436957 0.186900 82 1518
.. ... ... ... ... ... ...
726 0.254167 0.226642 0.652917 0.350133 247 1867
727 0.253333 0.255046 0.590000 0.155471 644 2451
728 0.253333 0.242400 0.752917 0.124383 159 1182
729 0.255833 0.231700 0.483333 0.350754 364 1432
730 0.215833 0.223487 0.577500 0.154846 439 2290
total_rentals
0 985
1 801
2 1349
3 1562
4 1600
.. ...
726 2114
727 3095
728 1341
729 1796
730 2729
[731 rows x 15 columns]
<Axes: xlabel='weekday', ylabel='mnth'>
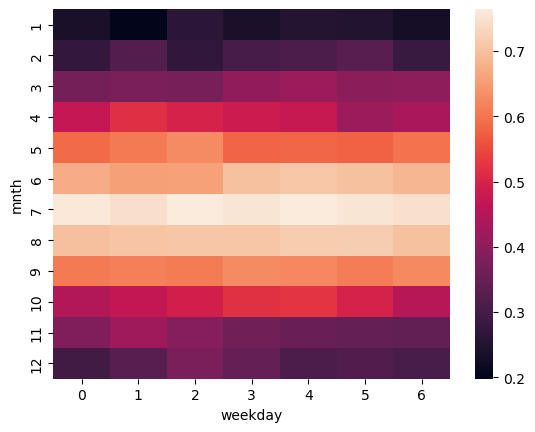
Indem die Heatmap angepasst wird, kann die Lesbarkeit verbessert und die Ableitung relevanter Erkenntnisse unterstützt werden. Dies zeigt das nachfolgende Codebeispiel.
temperature_crosstab = pd.crosstab(
index=temperature["mnth"],
columns=temperature["weekday"],
values=temperature["temp"],
aggfunc="mean"
)
sns.heatmap(temperature_crosstab, annot=True, cmap="YlGnBu", cbar=True, linewidths=.5)
<Axes: xlabel='weekday', ylabel='mnth'>
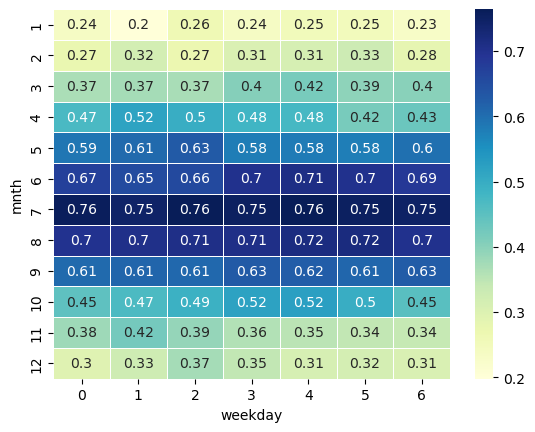
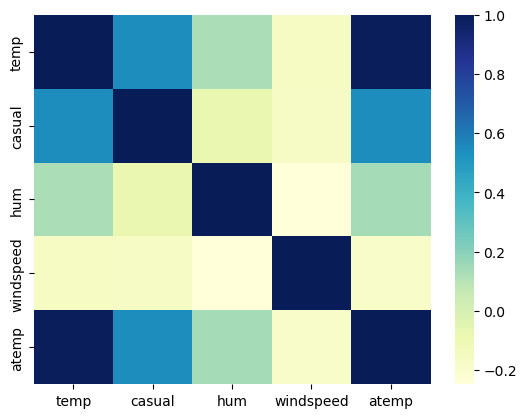
Wir können auch sehr einfach eine Korrelationsmatrix mithilfe von .corr() erstellen.
cols=["temp", "casual", "hum", "windspeed", "atemp"]
sns.heatmap(temperature[cols].corr(), cmap="YlGnBu" )
<Axes: >
Visualisierungen mit Plotly#
Plotly ist eine moderne Visualisierungsbibliothek für Python, die sich besonders durch ihre Interaktivität und Flexibilität auszeichnet. Im Gegensatz zu klassischen Bibliotheken wie Matplotlib oder Seaborn, die überwiegend statische Diagramme erzeugen, bietet Plotly die Möglichkeit, interaktive Grafiken zu erstellen, die sich dynamisch anpassen lassen. Das bedeutet, dass Nutzer in Diagramme hineinzoomen, Datenpunkte mit der Maus hervorheben oder zusätzliche Informationen in sogenannten Tooltips anzeigen können. Dies ist vor allem bei größeren Datensätzen hilfreich, da komplexe Strukturen und Zusammenhänge leichter erkundet werden können, ohne das Diagramm jedes Mal neu generieren zu müssen.
Ein weiterer Vorteil liegt in der Vielseitigkeit: Plotly unterstützt eine große Bandbreite an Diagrammtypen – von klassischen Balken- und Liniendiagrammen über Heatmaps und 3D-Darstellungen bis hin zu spezialisierten Visualisierungen wie Sankey-Diagrammen oder Karten. Darüber hinaus ist die Bibliothek nahtlos mit pandas-DataFrames integrierbar, was die Arbeit mit realen Datenquellen erheblich vereinfacht.
Der Nutzen von Plotly zeigt sich vor allem in interaktiven Analysen und Präsentationen. Während statische Plots für Berichte oder Publikationen oft ausreichend sind, erlaubt Plotly eine explorative Datenanalyse direkt im Notebook oder im Webbrowser. Analysten, Forschende und Entscheidungsträger können so Muster, Ausreißer und Trends schneller erkennen, indem sie direkt mit den Visualisierungen interagieren. Zusätzlich lassen sich Visualisierungen mit Plotly relativ einfach in Dash-Apps einbetten – einem Framework, das auf Plotly aufbaut und die Erstellung kompletter, interaktiver Datenanwendungen ermöglicht.
Insgesamt bietet Plotly eine sehr anwenderfreundliche Kombination aus ansprechender Darstellung, Interaktivität und breitem Funktionsspektrum. Dadurch eignet es sich besonders für Szenarien, in denen Daten nicht nur visualisiert, sondern auch aktiv erkundet und vermittelt werden sollen – sei es in der wissenschaftlichen Analyse, im Business-Reporting oder in datengetriebenen Webanwendungen. Nähere Informationen zu Plotly finden Sie unter 1, 2 und 3.
Wir installieren Plotly in unserer Umgebung mit folgendem Befehl:
conda install -c conda-forge plotly
pip install plotly
Anschließend können wir Plotly in unser Programm einbinden:
import plotly.express as px
Im nachfolgenden Codesbeispiel sehen wir, dass interaktive Interface von Plotly.
### Verbindung herstellen zwischen Plotly und Jupyter Notebook
import plotly.io as pio
import plotly.express as px
import plotly.offline as py
#pio.renderers.default = "plotly_mimetype"
#pio.renderers.default = "browser"
pio.renderers.default = "notebook" # oder "notebook_connected" für interaktive Version
import plotly.express as px
shares = ["BASF", "adidas", "Brenntag", "Fielmann", "Puma"]
dividend = [2.30, 3.07, 1.99, 1.40, 0.13]
fig=px.bar(x=shares, y=dividend, title="Dividenden deutscher Aktiengesellschaften in EUR")
fig.show()
Mit print(fig) können wir uns den Code anzeigen lassen.
print(fig)
Figure({
'data': [{'hovertemplate': 'x=%{x}<br>y=%{y}<extra></extra>',
'legendgroup': '',
'marker': {'color': '#636efa', 'pattern': {'shape': ''}},
'name': '',
'orientation': 'v',
'showlegend': False,
'textposition': 'auto',
'type': 'bar',
'x': array(['BASF', 'adidas', 'Brenntag', 'Fielmann', 'Puma'], dtype=object),
'xaxis': 'x',
'y': {'bdata': 'ZmZmZmZmAkCPwvUoXI8IQNejcD0K1/8/ZmZmZmZm9j+kcD0K16PAPw==', 'dtype': 'f8'},
'yaxis': 'y'}],
'layout': {'barmode': 'relative',
'legend': {'tracegroupgap': 0},
'template': '...',
'title': {'text': 'Dividenden deutscher Aktiengesellschaften in EUR'},
'xaxis': {'anchor': 'y', 'domain': [0.0, 1.0], 'title': {'text': 'x'}},
'yaxis': {'anchor': 'x', 'domain': [0.0, 1.0], 'title': {'text': 'y'}}}
})
Zähldiagramm#
Auch, wenn es auf den aller ersten Blick iritierend ist, der Befehl px.histogram() gibt uns ein Zähldiagramm aus, wie der nachfolgende Code demonstriert.
print(DAX_40.head())
fig=px.histogram(data_frame=DAX_40, x=DAX_40["Industrie"], nbins=10, title="Anzahl der DAX-Konzerne je Industriezweig", color="Industrie")
# Legende soll horizontal unter dem Diagramm sein
fig.update_layout(
width=1500, # mehr Breite
height=700,
showlegend=False
)
fig.show()
Unternehmen Industrie KGV \
0 SAP SE Software & IT Services 88,20
1 Siemens Aktiengesellschaft Machinery, Equipment & Components 17,23
2 Deutsche Telekom AG Telecommunications Services 12,73
3 Airbus SE Aerospace & Defense 28,89
4 Allianz SE Insurance 11,74
Kurs Börsenwert (Mio EUR) Konzern
0 231.95 252460.2 SAP SE
1 238.15 173740.9 Siemens
2 6.60 140764.9 Deutsche Telekom
3 179.50 132564.5 Airbus
4 35.80 130417.2 Allianz
Balkendiagramm#
Gerade beim Erstellen des Balkendiagrammes mit px.bar() sehen wir zum erstenmal deutlich den Vorteil von Plotly und dessen interaktiven Interface.
fig=px.bar(data_frame=DAX_40,
x=DAX_40["Industrie"],
y="Börsenwert (Mio EUR)",
color="Unternehmen",
hover_name="Börsenwert (Mio EUR)",
hover_data={"Börsenwert (Mio EUR)": ":,.0f"})
# Legende soll horizontal unter dem Diagramm sein
fig.update_layout(
width=1500, # mehr Breite
height=700,
legend=dict(
orientation="h",
yanchor="bottom",
y=-2.0,
xanchor="center",
x=0.5
))
fig.show()
Streudiagramme#
Streudiagramme lassen sich mithilfe von px.scatter() erzeugen.
fig=px.scatter(data_frame=alv_vol, x=alv_vol["Volumen"], y=alv_vol["Schluss"])
fig.show()
Liniendiagramm#
Mithilfe von px.line können wir ein Liniendiagramm uns ausgeben lassen und durch das interaktive Interface ist es möglich den gesamten Kursverlauf abzulesen.
print(concerns)
fig=px.line(data_frame=concerns, x=concerns["Datum"], y=concerns["Deutsche Bank"])
fig.show()
Datum Allianz Siemens Telekom BASF Deutsche Bank RWE
0 2020-09-10 183.16 117.62 15.355 54.51 7.995 32.16
1 2020-09-11 183.02 117.16 15.300 54.87 7.812 32.00
2 2020-09-14 182.58 116.84 15.245 55.23 7.901 31.49
3 2020-09-15 182.80 116.90 15.250 54.91 7.712 31.43
4 2020-09-16 181.80 118.68 15.230 55.06 7.866 31.56
... ... ... ... ... ... ... ...
1270 2025-09-03 353.00 229.45 31.110 44.63 29.800 33.98
1271 2025-09-04 354.10 230.05 31.840 44.00 30.260 34.66
1272 2025-09-05 351.40 226.00 31.650 43.81 29.870 35.02
1273 2025-09-08 352.70 230.65 30.450 44.18 30.030 35.82
1274 2025-09-09 353.30 228.50 30.610 43.51 30.535 35.71
[1275 rows x 7 columns]
Bemerkung: Das arbeiten mit plotly wird erst richtig interessant, wenn wir dash installieren und kleine Apps schreiben. Dies möchten wir an dieser Stelle nicht weiter intensiver und verweisen für Interessierte auf diese Quelle.
Eine sehr “schöne” Funktion von plotly ist das Nutzen von time buttons.
print(Kurs_ALV.tail())
fig = px.line(Kurs_ALV, x="Datum", y="Schlusskurs", title="Kursentwicklung Allianz")
date_buttons = [
dict(count=3, step="year", stepmode="backward", label="3Y"),
dict(count=1, step="year", stepmode="backward", label="1Y"),
dict(count=6, step="month", stepmode="backward", label="6M"),
dict(count=14, step="day", stepmode="backward", label="14D"),
dict(step="all", label="ALL")
]
fig.update_layout(
xaxis=dict(
rangeselector=dict(buttons=date_buttons),
rangeslider=dict(visible=True), # Baut einen Rangeslider ein
type="date"
)
)
fig.show()
Datum Schlusskurs Quartal
1270 2024-12-19 284.622162 2024Q4
1271 2024-12-20 282.417297 2024Q4
1272 2024-12-23 282.033844 2024Q4
1273 2024-12-27 282.896606 2024Q4
1274 2024-12-30 283.663513 2024Q4
Zusammenfassung der Graphik-Pakete Matplotlib, Seaborn und Plotly#
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
np.random.seed(42) #initialisiere Zufallsgenerator für reproduzierbare "Zufallsdaten"
Erzeugen uns Daten mit Funktionswerten von sin(x) und cos(x), zufällig gestört mit etwas normalverteilten Rauschen
# Beispieldaten erzeugen
x = np.linspace(0, 10, 50)
y1 = np.sin(x) + np.random.normal(scale=0.1, size=len(x))
y2 = np.cos(x) + np.random.normal(scale=0.1, size=len(x))
df = pd.DataFrame({
"x": np.concatenate([x, x]),
"y": np.concatenate([y1, y2]),
"Function": ["sin"]*len(x) + ["cos"]*len(x)
})
df
| x | y | Function | |
|---|---|---|---|
| 0 | 0.000000 | 0.049671 | sin |
| 1 | 0.204082 | 0.188842 | sin |
| 2 | 0.408163 | 0.461693 | sin |
| 3 | 0.612245 | 0.727009 | sin |
| 4 | 0.816327 | 0.705219 | sin |
| ... | ... | ... | ... |
| 95 | 9.183673 | -1.117426 | cos |
| 96 | 9.387755 | -0.969703 | cos |
| 97 | 9.591837 | -0.959973 | cos |
| 98 | 9.795918 | -0.931403 | cos |
| 99 | 10.000000 | -0.862530 | cos |
100 rows × 3 columns
type(df)
pandas.core.frame.DataFrame
df ist ein DataFrame im Tidy-Format, siehe beispielsweise tidy-format
# --- Matplotlib ---
plt.figure(figsize=(6,4))
for func in df["Function"].unique():
subset = df[df["Function"] == func]
plt.plot(subset["x"], subset["y"], label=func)
plt.title("Matplotlib")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
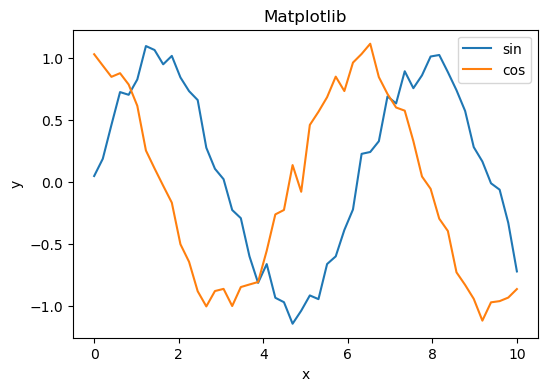
# --- Seaborn ---
plt.figure(figsize=(6,4))
sns.lineplot(data=df, x="x", y="y", hue="Function")
plt.title("Seaborn")
plt.show()
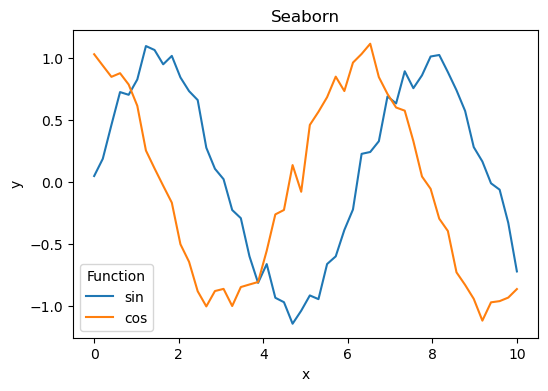
# --- Plotly ---
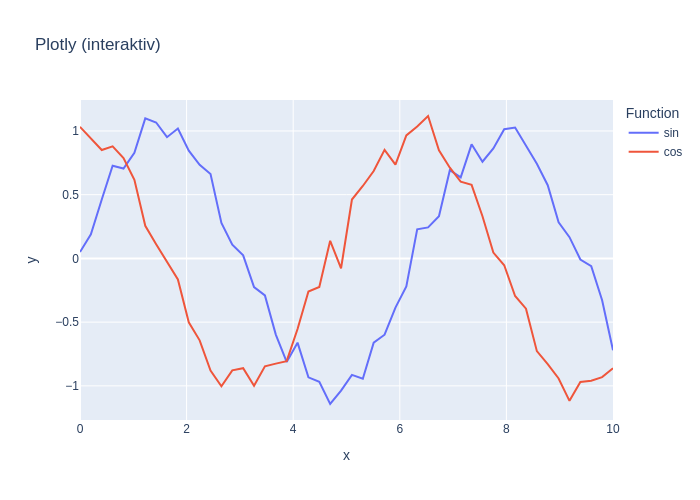
fig = px.line(df, x="x", y="y", color="Function", title="Plotly (interaktiv)")
fig.show()
fig.write_image("plotly_bsp.png")
Die Interaktion ist insbesondere in Browsern sinnvoll. Fährt man nun mit dem Mauszeiger über die Graphen, erhält man Infos über die Datenwerte angezeigt oder kann in die Graphiken hinein- oder herauszoomen. Klinckt man in die Legende, können einzelne Funktionen ausgeschaltet werden.
Achtung: Plotly nicht für pdf-Version von jupyter-notebook verfügbar – daher wird hier die interaktive Graphik in eine Bilddatei umgewandlet und als Alternative hier eingebunden: