 und dem Empfänger
und dem Empfänger  existiert. Ein vermeintlich sicherer Kanal kann natürlich ein großer Unsicherheitsfaktor sein.
existiert. Ein vermeintlich sicherer Kanal kann natürlich ein großer Unsicherheitsfaktor sein.| AES | ElGamal |
Bisher wurde immer vorausgesetzt, dass ein sicherer Kanal zum Austausch des geheimen Schlüssels zwischen beiden Parteien, etwa dem Sender  und dem Empfänger
und dem Empfänger  existiert. Ein vermeintlich sicherer Kanal kann natürlich ein großer Unsicherheitsfaktor sein.
existiert. Ein vermeintlich sicherer Kanal kann natürlich ein großer Unsicherheitsfaktor sein.
Ein weiteres Problem ist, dass bisher der geheime Schlüssel nur den beiden Teilnehmern  und
und  bekannt war. Ein Dritter, etwa
bekannt war. Ein Dritter, etwa  , konnte keine Nachricht an
, konnte keine Nachricht an 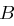 verschlüsselt übermitteln, die auch von
verschlüsselt übermitteln, die auch von  hätte korrekt entschlüsselt werden können.
hätte korrekt entschlüsselt werden können.
Diffie und Hellman schlugen daher 1976 vor, Systeme zu suchen bzw. zu entwickeln, bei denen ein Teil des Schlüssels öffentlich ist ( kann an
kann an  senden, wenn ein Teil von
senden, wenn ein Teil von  's Schlüssel öffentlich ist) und der andere Teil des Schlüssels privat und geheim ist. Derartige Kryptosysteme werden Public-Key-Systeme (oder auch asymmetrische Kryptosysteme) genannt.
's Schlüssel öffentlich ist) und der andere Teil des Schlüssels privat und geheim ist. Derartige Kryptosysteme werden Public-Key-Systeme (oder auch asymmetrische Kryptosysteme) genannt.
Ist der Schlüssel von  allgemein bekannt, so kann jeder an
allgemein bekannt, so kann jeder an  Nachrichten (verschlüsselt) senden! In diesem Fall ist kein sicherer Kanal zur Schlüsselübergabe mehr notwendig.
Nachrichten (verschlüsselt) senden! In diesem Fall ist kein sicherer Kanal zur Schlüsselübergabe mehr notwendig.
Nach einer Idee von Rivest, Shamir und Adleman entstand das RSA-System, benannt nach den Anfangsbuchstaben der Namen der drei Erfinder.
Wir nehmen im Folgenden an, dass der Klartext eine Folge von Bits ist, die in Blöcke gleicher Länge unterteilt wird. Jeder Block, interpretiert als natürliche Zahl, wird einzeln verschlüsselt.
Die Funktionsweise des RSA-Kryptosystems lässt sich wie folgt beschreiben.
Sei  eine Nachricht, die verschlüsselt von
eine Nachricht, die verschlüsselt von  an
an  gesandt werden soll. Die Nachricht
gesandt werden soll. Die Nachricht  ist in natürlicher Weise (etwa mit der Binärdarstellung) aus einem
ist in natürlicher Weise (etwa mit der Binärdarstellung) aus einem  -Klartextblock der Länge maximal
-Klartextblock der Länge maximal  entstanden. Später werden wir sehen, dass wir beliebige Nachrichten
entstanden. Später werden wir sehen, dass wir beliebige Nachrichten  verwenden können.
verwenden können.
 erzeugt zwei große Primzahlen
erzeugt zwei große Primzahlen  und
und  mit
mit  .
. berechnet die Produkte
berechnet die Produkte  sowie
sowie 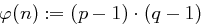 .
. erzeugt eine natürliche Zahl
erzeugt eine natürliche Zahl  mit
mit  und
und  .
. berechnet die (eindeutige) Zahl
berechnet die (eindeutige) Zahl  mit
mit  , also ist
, also ist  das multiplikativ Inverse von
das multiplikativ Inverse von  in
in  .
. veröffentlicht die Zahlen
veröffentlicht die Zahlen  und
und  . Dann ist das Paar
. Dann ist das Paar  der öffentliche Schlüssel und das Paar
der öffentliche Schlüssel und das Paar  der private geheime Schlüssel von
der private geheime Schlüssel von  .
. möchte an
möchte an  eine Nachricht
eine Nachricht  senden. Dazu nimmt er den öffentlichen Schlüssel
senden. Dazu nimmt er den öffentlichen Schlüssel  von
von 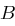 , berechnet
, berechnet

und sendet das Ergebnis an  .
.
Empfängt  die Nachricht
die Nachricht  (
( ) von
) von  , so nimmt er seinen geheimen privaten Schlüssel
, so nimmt er seinen geheimen privaten Schlüssel 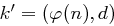 und berechnet
und berechnet

und erhält die gesendete Nachricht 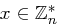 . Dieses müssen wir natürlich noch verifizieren, zu diesem Zweck weisen wir die Korrektheit des RSA-Verfahrens nach.
. Dieses müssen wir natürlich noch verifizieren, zu diesem Zweck weisen wir die Korrektheit des RSA-Verfahrens nach.
Wir wollen zeigen, dass man für alle  , die wie beschrieben verschlüsselt und anschließend wieder entschlüsselt werden, genau die Nachricht
, die wie beschrieben verschlüsselt und anschließend wieder entschlüsselt werden, genau die Nachricht  erhält, dass also gilt:
erhält, dass also gilt:

Mit dem Satz von Euler und Satz 41 sieht man nun für die Nachricht  die Korrektheit des RSA-Verfahrens wie folgt ein:
die Korrektheit des RSA-Verfahrens wie folgt ein:

da nach Annahme  gilt.
gilt.
Ein wichtiger Aspekt beim RSA-Verfahren ist das effiziente Auffinden geeigneter Primzahlen  und
und  . Dies ist mit verschiedenen probabilistischen Primzahlverfahren wie etwa der Methode von Solovay und Strassen effizient möglich.
. Dies ist mit verschiedenen probabilistischen Primzahlverfahren wie etwa der Methode von Solovay und Strassen effizient möglich.
Wir wollen kurz einige Überlegungen zur Effizienz bzw. Laufzeit des RSA-Systems durchführen.
Beim Setup des Systems benötigen wir eine effiziente Erzeugung zweier großer Primzahlen, die wir wie erwähnt beispielsweise mit dem Algorithmus von Solovay und Strassen durchführen können. Seit einiger Zeit ist sogar ein polynomieller deterministischer Algorithmus zum Primzahltest bekannt, aber der Algorithmus von Solovay und Strassen ist aufgrund von kleinen Konstanten in der Laufzeit besonders schnell.
Desweiteren entsteht im Wesentlichen Aufwand durch die Multiplikation zweier langer Zahlen sowie durch Aufrufe des Euklidischen Algorithmus zur Bestimmung des größten gemeinsamen Teilers zweier Zahlen bzw. durch Aufrufe des erweiterten Euklidischen Algorithmus zur Bestimmung des multiplikativen Inversen einer Zahl. Mit der Schulmethode kann das Produkt zweier  -Bit Zahlen mit Aufwand
-Bit Zahlen mit Aufwand  bestimmt werden, also effizient in der Eingabelänge. Für den Euklidischen Algorithmus überlegt man sich, dass dieser aufgerufen auf Zahlen
bestimmt werden, also effizient in der Eingabelänge. Für den Euklidischen Algorithmus überlegt man sich, dass dieser aufgerufen auf Zahlen  höchstens
höchstens  viele Iterationen mit Zeitaufwand jeweils
viele Iterationen mit Zeitaufwand jeweils  benötigt, was einen Aufwand von
benötigt, was einen Aufwand von  , also ebenfalls polynomiell in der Eingabelänge bedeutet. Bis auf die Tatsache, dass wir beim Setup Zahlen auswürfeln und unter Umständen mehrere Versuche benötigen, bis geeignete Zahlen gefunden sind, lassen sich die Schritte des Setups also effizient ausführen.
, also ebenfalls polynomiell in der Eingabelänge bedeutet. Bis auf die Tatsache, dass wir beim Setup Zahlen auswürfeln und unter Umständen mehrere Versuche benötigen, bis geeignete Zahlen gefunden sind, lassen sich die Schritte des Setups also effizient ausführen.
Dass man beim "Auswürfeln von Primzahlen" nicht zu viele Versuche benötigt kann man mit einem Satz aus der Zahlentheorie zeigen, der besagt dass die Anzahl der Primzahlen der Größe höchstens  ungefähr
ungefähr  ist. Damit gibt es unter allen
ist. Damit gibt es unter allen  -stelligen Binärzahlen im wesentlichen
-stelligen Binärzahlen im wesentlichen
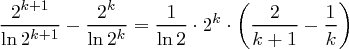
viele Primzahlen. Also können wir folgern, dass die Wahrscheinlichkeit, beim Auswürfeln einer  -Bit Zahl eine Primzahl zu erhalten,
-Bit Zahl eine Primzahl zu erhalten,  ist. Wir benötigen daher im Erwartungswert
ist. Wir benötigen daher im Erwartungswert  viele Zufallsexperimente, um eine Primzahl der Länge
viele Zufallsexperimente, um eine Primzahl der Länge  zu erhalten.
zu erhalten.
Bei der Ver- und Entschlüsselung entsteht Aufwand durch das Potenzieren langer Zahlen. Da wir alle Rechnungen modulo  durchführen, besitzen alle Zwischenergebnisse diese Maximallänge, und eine Multiplikation lässt sich polynomiell in der Eingabelänge durchführen. Die Potenzen berechnet man nun mit der Methode des fortgesetzten Quadrierens. Dazu benutzt man die Identität
durchführen, besitzen alle Zwischenergebnisse diese Maximallänge, und eine Multiplikation lässt sich polynomiell in der Eingabelänge durchführen. Die Potenzen berechnet man nun mit der Methode des fortgesetzten Quadrierens. Dazu benutzt man die Identität  . Wollen wir
. Wollen wir  berechnen für eine
berechnen für eine  -Bit-Zahl
-Bit-Zahl 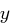 in Binärdarstellung,
in Binärdarstellung,  , so berechnen wir
, so berechnen wir  und multiplizieren die Terme zu den Potenzen, für die
und multiplizieren die Terme zu den Potenzen, für die  gilt. Damit kommen wir mit höchstens
gilt. Damit kommen wir mit höchstens  vielen Multiplikationen aus und die Potenzierung lässt sich effizient durchführen.
vielen Multiplikationen aus und die Potenzierung lässt sich effizient durchführen.
Die Sicherheit des RSA-Systems beruht auf der (höchstwahrscheinlich korrekten) Annahme, dass die Faktorisierung einer Zahl  nicht effizient durchführbar ist, also nicht in Zeit
nicht effizient durchführbar ist, also nicht in Zeit  . Auch ist es schwierig, in
. Auch ist es schwierig, in  Wurzeln, etwa die
Wurzeln, etwa die  -te,
-te,  , zu ziehen. In
, zu ziehen. In  Wurzeln zu ziehen ist jedoch bei ganzzahligem Ergebnis einfach, da man die binäre Suche anwenden kann.
Wurzeln zu ziehen ist jedoch bei ganzzahligem Ergebnis einfach, da man die binäre Suche anwenden kann.
Wir betrachten nun einige Fälle, bei denen ein Angreifer über verschiedene Informationen verfügt und prüfen, wie diese zum Brechen des Kryptosystems verwendet werden können:
 und
und  mit
mit  . Dann kann er auch
. Dann kann er auch  leicht berechnen. (Die Anzahl der zu
leicht berechnen. (Die Anzahl der zu  teilerfremden Zahlen
teilerfremden Zahlen  ist gleich
ist gleich  .)
.)
Kennt der Gegner  , so kann er mit dem Euklidischen Algorithmus aus
, so kann er mit dem Euklidischen Algorithmus aus  auch den geheimen Schlüssel
auch den geheimen Schlüssel  , also
, also  , in Polynomialzeit berechnen und so die Nachricht korrekt entschlüsseln. Daher gehört der Wert
, in Polynomialzeit berechnen und so die Nachricht korrekt entschlüsseln. Daher gehört der Wert  zum geheimen Schlüssel
zum geheimen Schlüssel  .
.
 folgt
folgt


 , etwa durch Raten oder Probieren bei kleinen Werten von
, etwa durch Raten oder Probieren bei kleinen Werten von  , so kann er das Gleichungssystem
, so kann er das Gleichungssystem

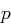 und
und  auflösen: Sei o.B.d.A.
auflösen: Sei o.B.d.A.  , dann folgt
, dann folgt  und somit
und somit 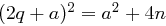 , also
, also  . Die Differenz
. Die Differenz  sollte also nicht zu klein gewählt werden, um ein Raten für den Angreifer zu erschweren. Falls gilt
sollte also nicht zu klein gewählt werden, um ein Raten für den Angreifer zu erschweren. Falls gilt  , so ist die Faktorisierung von
, so ist die Faktorisierung von 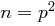 mit Wurzelziehen einfach durchzuführen.
mit Wurzelziehen einfach durchzuführen.
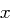 an verschiedene Adressaten
an verschiedene Adressaten  mit
mit  gesendet und werden dabei die öffentlichen Schlüssel
gesendet und werden dabei die öffentlichen Schlüssel  mit
mit  für alle
für alle  verwendet - also haben alle öffentlichen Schlüssel die gleiche zweite Komponente und diese ist identisch mit der Anzahl der Empfänger - so kann ein Gegner die verschlüsselte Nachricht leicht entschlüsseln. Dieses erfolgt effizient mit dem Chinesischen Restsatz (siehe Satz 32).
verwendet - also haben alle öffentlichen Schlüssel die gleiche zweite Komponente und diese ist identisch mit der Anzahl der Empfänger - so kann ein Gegner die verschlüsselte Nachricht leicht entschlüsseln. Dieses erfolgt effizient mit dem Chinesischen Restsatz (siehe Satz 32).
Die Situation, dass die Zahlen 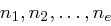 paarweise teilerfremd sind, ist nicht so unwahrscheinlich, da etwa eine Folge von Primzahlen diese Eigenschaft hat! Sind die verschlüsselten Nachrichten
paarweise teilerfremd sind, ist nicht so unwahrscheinlich, da etwa eine Folge von Primzahlen diese Eigenschaft hat! Sind die verschlüsselten Nachrichten  mit
mit

 und auch die Moduli
und auch die Moduli  dem Gegner bekannt, so berechnet dieser in Polynomialzeit mit dem Chinesischen Restsatz das eindeutige
dem Gegner bekannt, so berechnet dieser in Polynomialzeit mit dem Chinesischen Restsatz das eindeutige 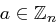 mit
mit  derart, dass
derart, dass

 gilt. Mit
gilt. Mit  sowie
sowie  ,
,  , für die Nachricht
, für die Nachricht  wegen der Injektivität bei der Verschlüsselung, also
wegen der Injektivität bei der Verschlüsselung, also  , folgt
, folgt  . Damit kann durch einfaches Ziehen der
. Damit kann durch einfaches Ziehen der  -ten Wurzel (in
-ten Wurzel (in  !)
!)  berechnet und damit leicht entschlüsselt werden. (Die
berechnet und damit leicht entschlüsselt werden. (Die  -te Wurzel in
-te Wurzel in  einer natürlichen Zahl kann leicht und effizient mit binärer Suche ermittelt werden.)
einer natürlichen Zahl kann leicht und effizient mit binärer Suche ermittelt werden.)
Frage: Handelt es sich statt einer Nachricht  um verschiedene Nachrichten
um verschiedene Nachrichten  , so kann diese Technik nicht erfolgreich eingesetzt werden. Warum nicht?
, so kann diese Technik nicht erfolgreich eingesetzt werden. Warum nicht?
 für eine Nachricht
für eine Nachricht  , so kann zunächst eventuell nicht korrekt entschlüsselt werden, da wir für den Nachweis den Satz von Euler mit
, so kann zunächst eventuell nicht korrekt entschlüsselt werden, da wir für den Nachweis den Satz von Euler mit  benutzt haben. Aber da
benutzt haben. Aber da  das Produkt zweier verschiedener Primzahlen ist, wie hier gegeben, gilt Satz 43:
das Produkt zweier verschiedener Primzahlen ist, wie hier gegeben, gilt Satz 43:
Für  und
und  ist
ist

 , wobei
, wobei 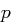 und
und  verschiedene Primzahlen sind.
verschiedene Primzahlen sind.
Beim RSA-System können wir also beliebige Zahlen  zum Verschlüsseln verwenden, und nicht nur Zahlen
zum Verschlüsseln verwenden, und nicht nur Zahlen  .
.
Frage: Gilt die Aussage " " auch, wenn
" auch, wenn  Produkt von mehreren paarweise verschiedenen Primzahlen ist?
Produkt von mehreren paarweise verschiedenen Primzahlen ist?
Wir wollen nun noch einmal zum ersten Gliederungspunkt zurückkommen und Möglichkeiten für einen Angriff durch Faktorisierung diskutieren. Als Beispiel eines Verfahrens zur Faktorisierung natürlicher Zahlen wird hier der  -Algorithmus von Pollard (1974) vorgestellt.
-Algorithmus von Pollard (1974) vorgestellt.
Idee beim Verfahren: Ist  eine Primzahl mit
eine Primzahl mit  und
und  für jede Primzahlpotenz
für jede Primzahlpotenz  mit
mit  , dann gilt
, dann gilt  . Diese Aussage ist folgendermaßen begründet: Für die Primfaktorenzerlegung
. Diese Aussage ist folgendermaßen begründet: Für die Primfaktorenzerlegung 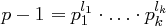 und
und  für
für  gilt
gilt  für
für  , und somit folgt aus
, und somit folgt aus  für
für  auch
auch  . Speziell ist dieses Verfahren für Zahlen
. Speziell ist dieses Verfahren für Zahlen  geeignet, bei denen
geeignet, bei denen  kleine Primfaktoren enthält.
kleine Primfaktoren enthält.
 -Algorithmus:
-Algorithmus:
Eingabe:  sowie eine Schranke
sowie eine Schranke  .
.
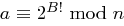 . Dieses kann etwa so erfolgen:
. Dieses kann etwa so erfolgen: ; for
; for 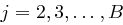 do
do  .
. sind auch weitere Werte
sind auch weitere Werte  möglich!]
möglich!] .
.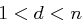 , dann ist die Ausgabe "
, dann ist die Ausgabe " ist Faktor von
ist Faktor von  ",
", gefunden".
gefunden".Die Korrektheit ist offensichtlich. Falls  gilt, so ist
gilt, so ist  , also
, also  , wobei
, wobei 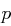 ein Primfaktor von
ein Primfaktor von  ist.
ist.
Laufzeit: Im ersten Schritt zur Berechnung von  führt man
führt man 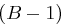 modulare Exponentiationen jeweils
modulare Exponentiationen jeweils  aus, jede kann mit maximal
aus, jede kann mit maximal  modularen Multiplikationen durchgeführt werden. Das Rechnen modulo
modularen Multiplikationen durchgeführt werden. Das Rechnen modulo 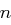 kann insgesamt in Zeit
kann insgesamt in Zeit  durchgeführt werden. Im zweiten Schritt kann der
durchgeführt werden. Im zweiten Schritt kann der  in Zeit
in Zeit  mit dem Euklidischen Algorithmus berechnet werden.
mit dem Euklidischen Algorithmus berechnet werden.
Für die Gesamtzeit  erhalten wir daher die obere Schranke
erhalten wir daher die obere Schranke

Für  ist
ist  , also Polynomialzeit, aber die Erfolgswahrscheinlichkeit für das Finden eines Teilers ist eventuell klein.
, also Polynomialzeit, aber die Erfolgswahrscheinlichkeit für das Finden eines Teilers ist eventuell klein.
Definition 5 (Las Vegas / Monte Carlo Algorithmus)
Sei  fest. Ein Las Vegas Algorithmus ist ein probabilistisches Verfahren, welches zu jeder (zulässigen) Eingabe mit Wahrscheinlichkeit höchstens
fest. Ein Las Vegas Algorithmus ist ein probabilistisches Verfahren, welches zu jeder (zulässigen) Eingabe mit Wahrscheinlichkeit höchstens  keine Antwort gibt ("weiss nicht"), aber sonst eine korrekte Antwort liefert.
keine Antwort gibt ("weiss nicht"), aber sonst eine korrekte Antwort liefert.
Ein Monte Carlo Algorithmus liefert immer eine Antwort, die mit Wahrscheinlichkeit höchstens  falsch sein kann.
falsch sein kann.
Bemerkung: Wird ein Las Vegas Algorithmus mit Parameter  nun
nun 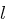 -mal gestartet (Multi-Start-Ansatz), so liefert er mit Wahrscheinlichkeit höchstens
-mal gestartet (Multi-Start-Ansatz), so liefert er mit Wahrscheinlichkeit höchstens  jedesmal keine Antwort. Eine korrekte Antwort erfolgt also mit Wahrscheinlichkeit mindestens
jedesmal keine Antwort. Eine korrekte Antwort erfolgt also mit Wahrscheinlichkeit mindestens 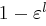 .
.
Für  erhält man also schon bei 10 Starts eine Antwort mit Wahrscheinlichkeit mindestens
erhält man also schon bei 10 Starts eine Antwort mit Wahrscheinlichkeit mindestens  .
.
Satz 6
Ein Algorithmus, der zu gegebenem öffentlichen Schlüssel  im RSA-System den geheimen Schlüssel
im RSA-System den geheimen Schlüssel  berechnet, liefert einen Las Vegas Algorithmus mit Parameter
berechnet, liefert einen Las Vegas Algorithmus mit Parameter  zur Faktorisierung von
zur Faktorisierung von  .
.
Beweis Zunächst machen wir einige Vorbemerkungen. Sei  Produkt zweier ungerader Primzahlen
Produkt zweier ungerader Primzahlen  und
und  mit
mit  . Es gilt dann:
. Es gilt dann:

 vier Lösungen hat. Also gibt es neben den trivialen Lösungen
vier Lösungen hat. Also gibt es neben den trivialen Lösungen  und
und  noch zwei weitere nichttriviale Lösungen. Diese findet man mit dem Chinesischen Restsatz, durch Lösen der simultanen Kongruenzen
noch zwei weitere nichttriviale Lösungen. Diese findet man mit dem Chinesischen Restsatz, durch Lösen der simultanen Kongruenzen  und
und  oder
oder  und
und  .
.
Sei  nichttriviale Lösung von
nichttriviale Lösung von  . Dann gilt
. Dann gilt

 oder
oder  und analog ist
und analog ist  gleich
gleich  oder
oder  . Die größten gemeinsamen Teiler können mit dem Euklidischen Algorithmus berechnet werden.
. Die größten gemeinsamen Teiler können mit dem Euklidischen Algorithmus berechnet werden.
Kennt man also eine nichtriviale Lösung der Kongruenz  , so erhält man mit polynomiellem Zeitaufwand die Faktorisierung von
, so erhält man mit polynomiellem Zeitaufwand die Faktorisierung von  . Wir haben daher den folgenden Algorithmus:
. Wir haben daher den folgenden Algorithmus:
Algorithmus Faktorisierung bei gegebenem öffentlichen Schlüssel 
Gegeben: Ein Algorithmus, der zu gegebenen Werten 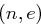 mit
mit  für Primzahlen
für Primzahlen  ein
ein  berechnet mit
berechnet mit 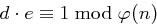 , wobei
, wobei  Produkt zweier verschiedener Primzahlen ist.
Produkt zweier verschiedener Primzahlen ist.
Gesucht: Faktorisierung von  .
.
 zufällig.
zufällig.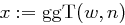 .
. , dann ist die Ausgabe "Faktoren von
, dann ist die Ausgabe "Faktoren von 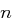 sind
sind  und
und  ", STOP.
", STOP.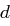 mit gegebenem Algorithmus, wobei
mit gegebenem Algorithmus, wobei  gilt.
gilt. mit
mit  , wobei
, wobei  ungerade ist.
ungerade ist.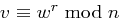 .
. , dann ist die Ausgabe "keine Antwort", STOP.
, dann ist die Ausgabe "keine Antwort", STOP. do
do .
. ist, dann ist die Ausgabe "keine Antwort", STOP;
ist, dann ist die Ausgabe "keine Antwort", STOP; und die Ausgabe ist "Faktoren sind
und die Ausgabe ist "Faktoren sind  und
und  ".
".Bemerkungen:
 oder
oder  gilt, so folgt
gilt, so folgt 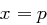 oder
oder  .
.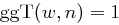 , so wird berechnet
, so wird berechnet  bis gilt
bis gilt  , wobei
, wobei 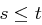 ist wegen
ist wegen  .
. und
und  . Für
. Für  erfolgt die Ausgabe "keine Antwort", sonst ist
erfolgt die Ausgabe "keine Antwort", sonst ist  nichttriviale Quadratwurzel von
nichttriviale Quadratwurzel von  , und die Faktorisierung von
, und die Faktorisierung von  ist möglich. Das Verfahren liefert offenbar korrekte Antworten.
ist möglich. Das Verfahren liefert offenbar korrekte Antworten.Beweis Der Algorithmus liefert keine Antwort (schlechte Wahl von  ), wenn eine der Aussagen gilt:
), wenn eine der Aussagen gilt:
Wir zählen im folgenden die Anzahl der Lösungen der einzelnen Kongruenzen für  für Primzahlen
für Primzahlen  .
.
zu 1.: Gilt  , so gilt auch
, so gilt auch  und
und  . Andererseits können Lösungen von
. Andererseits können Lösungen von  und
und  mit dem Chinesischem Restsatz zu einer Lösung
mit dem Chinesischem Restsatz zu einer Lösung  kombiniert werden. Wir betrachten daher die Anzahl der Lösungen der einzelnen Kongruenzen
kombiniert werden. Wir betrachten daher die Anzahl der Lösungen der einzelnen Kongruenzen  sowie
sowie  .
.
Zunächst betrachten wir die Kongruenz  . Sei
. Sei  erzeugendes Element von
erzeugendes Element von  , also ist
, also ist  für ein
für ein  . Dann gilt
. Dann gilt  , also nach dem Satz von Fermat
, also nach dem Satz von Fermat


 und
und


 und
und  .
.
Mit  folgt
folgt  , also
, also 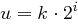 , da
, da 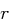 ungerade ist. Mit
ungerade ist. Mit 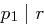 und
und 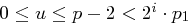 folgt, dass
folgt, dass  möglich ist. Die Anzahl Lösungen von
möglich ist. Die Anzahl Lösungen von  ist daher maximal
ist daher maximal  . Entsprechend gilt, dass die Anzahl Lösungen von
. Entsprechend gilt, dass die Anzahl Lösungen von  maximal
maximal 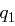 ist. Die Anzahl Lösungen der Kongruenz
ist. Die Anzahl Lösungen der Kongruenz  ist daher maximal
ist daher maximal 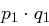 .
.
zu 2.: Wir bestimmen nun für  die Anzahl Lösungen der Kongruenz
die Anzahl Lösungen der Kongruenz
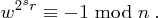
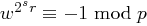 und
und  .
.
Für 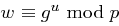 und
und  folgt
folgt  . Da
. Da 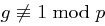 erzeugendes Element in
erzeugendes Element in  ist, gilt
ist, gilt  , also nach dem Satz von Fermat
, also nach dem Satz von Fermat
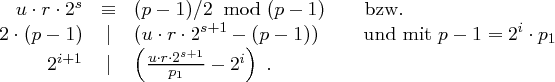
 gibt es hier keine Lösungen. Für
gibt es hier keine Lösungen. Für  sind die Lösungen
sind die Lösungen  genau ungerade Vielfache von
genau ungerade Vielfache von 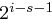 , da
, da  ungerade ist. Die Anzahl dieser Vielfachen ist
ungerade ist. Die Anzahl dieser Vielfachen ist

 . Damit ist die Anzahl Lösungen von
. Damit ist die Anzahl Lösungen von  maximal
maximal

 ist die Anzahl der schlechten Wahlen von
ist die Anzahl der schlechten Wahlen von  daher maximal
daher maximal
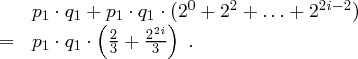
Mit  (da
(da 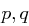 ungerade) haben wir
ungerade) haben wir


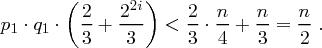
 gemäß der Gleichverteilung wählen, sind mindestens
gemäß der Gleichverteilung wählen, sind mindestens  gute Wahlen für
gute Wahlen für  dabei, also ist die Erfolgswahrscheinlichkeit mindestens
dabei, also ist die Erfolgswahrscheinlichkeit mindestens  .
.
Aufgabe 1
Beim RSA-Verfahren verwendet jemand als öffentliche Schlüssel  und
und  , wobei
, wobei  ein Produkt zweier verschiedener Primzahlen
ein Produkt zweier verschiedener Primzahlen  ist. Welche Probleme treten auf?
ist. Welche Probleme treten auf?
Aufgabe 2
Eine Nachricht 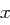 wird mittels RSA verschlüsselt und an
wird mittels RSA verschlüsselt und an 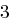 Empfänger mit den öffentlichen Schlüsseln
Empfänger mit den öffentlichen Schlüsseln  ,
,  und
und  gesendet. Bestimmen Sie aus den Chiffraten
gesendet. Bestimmen Sie aus den Chiffraten

die ursprüngliche Nachricht  .
.
Aufgabe 3
Sei  ein öffentlicher RSA-Schlüssel und
ein öffentlicher RSA-Schlüssel und

das Chiffrat zu einem Klartext  . Zeigen Sie, dass eine natürliche Zahl
. Zeigen Sie, dass eine natürliche Zahl  mit
mit

existiert. Kann diese Aussage einem Angreifer helfen?
Aufgabe 4
Ein Klartext  wird zweimal mit den öffentlichen Schlüsseln
wird zweimal mit den öffentlichen Schlüsseln  und
und  verschlüsselt. Kann, wenn
verschlüsselt. Kann, wenn  ist, ein Angreifer aus den Chiffraten
ist, ein Angreifer aus den Chiffraten

den Klartext bestimmen?
Hinweis: Zu  existieren
existieren  mit
mit  (vgl. Bemerkung 20 (iv)).
(vgl. Bemerkung 20 (iv)).
Aufgabe 5
Zeigen Sie, dass man mit der RSA-Dechiffrierfunktion  tatsächlich den Klartext
tatsächlich den Klartext  erhält.
erhält.
Aufgabe 6
Zur Beschleunigung der Dechiffrierung bei einem RSA-System mit den Parametern  führt der Empfänger eines Chiffrats
führt der Empfänger eines Chiffrats  folgendes aus:
folgendes aus:
Er berechnet  sowie
sowie  und berechnet mit dem Chinesischen Restsatz ein
und berechnet mit dem Chinesischen Restsatz ein  mit
mit

Ist  die gesendete Nachricht?
die gesendete Nachricht?
Aufgabe 7
Von einer natürlichen Zahl  sei bekannt, dass sie das Produkt zweier verschiedener Primzahlen ist.
sei bekannt, dass sie das Produkt zweier verschiedener Primzahlen ist.
Aufgabe 8
Beim Setup des RSA-Systems werden versehentlich die gleichen Primzahlen  und
und  gewählt.
gewählt.
 ?
?
Aufgabe 9
Im RSA-System mit öffentlichem Schlüssel  heißt eine Nachricht
heißt eine Nachricht  ein Fixpunkt, wenn gilt
ein Fixpunkt, wenn gilt

 auch
auch  ein Fixpunkt ist.
ein Fixpunkt ist. gleich
gleich  ist.
ist.Hinweis: Es gibt für Primzahlen  ein erzeugendes Element
ein erzeugendes Element  mit
mit  .
.
Aufgabe 10
Betrachten Sie folgenden Primzahltest. In dem Intervall  , wobei der Einfachheit halber
, wobei der Einfachheit halber  durch
durch  teilbar ist, wird zufällig gemäß der Gleichverteilung eine natürliche Zahl
teilbar ist, wird zufällig gemäß der Gleichverteilung eine natürliche Zahl  ausgewählt. Sodann wird geprüft, ob die Zahl
ausgewählt. Sodann wird geprüft, ob die Zahl  durch
durch  ,
,  oder
oder  teilbar ist. Ist dieses der Fall, so wird die Antwort "keine Primzahl" gegeben, ansonsten die Antwort "wahrscheinlich eine Primzahl".
teilbar ist. Ist dieses der Fall, so wird die Antwort "keine Primzahl" gegeben, ansonsten die Antwort "wahrscheinlich eine Primzahl".
Bestimmen Sie die Fehlerwahrscheinlichkeit dieses Tests.