Chemnitz FEM Symposium 2001

[ Announcement | Programme | List of participants ]

Collection of abstracts

One of the strengths of DG Galerkin Methods is that the semidiscrete o.d.e. system is explicit for transient problems. In contrast the standard mass matrix is such that positivity of the solution may be violated in a transient problem. In this talk an attempt is made to use some of the ideas employed in nonlinear DG and Petrov Galerkin schemes and also in Finite Volume schemes to solve this problem. As a result it is possible to show how this results in positive solutions for hyperbolic problems. The central idea extends in a straightforward manner to unstructured triangular and tetrahedral meshes. Numerical examples are used to show the benefits and also the potential drawbacks of the approach.

References:

[1] M. Berzins, Modified Mass Matrices and Positivity Preservation for PDEs. Communications in Numerical Methods in Engineering, 2001, to appear.

This presentation will consist of a mixture of known results, examples, techniques, conjectures and open problems connected to superconvergence questions in mixed finite element methods. One of its intentions is to provoke the audience into adding topics to the list, which would motivate the speaker to finally write a survey paper in this field. Another intention is, of course, to advertise some own results, and to ask for suggestions and remarks that could be useful in tackling the open problems.

References:

Most of the material presented can be found in detail on my Homepage, http://www.math.uu.nl/people/brandts.

The evolution of a slightly compressible viscous flow over a dihedral plane gives rise to the creation of recirculation areas and vortices generation. These phenomena are damaging for the aerodynamic properties of the configuration. This work is devoted to the numerical implementation and to the comparison of four active control techniques in order to increase the upward thrust induced by the fluid on the dihedral, by local modification of the boundary conditions. The two-dimensional Navier-Stokes equations are solved by a direct numerical simulation code based on a mixed finite volumes / finite elements scheme with an explicit time integration on unstructured mesh. Pressure tangent gradient sensors on the dihedral as well as vortex generator jets to blow or suck up fluid through the wall are used for all of the four active control techniques involved.

The closed-loop control simply consists in an amplification between the signal recorded at a sensor located downstream in the flow and the jet produced at an actuator located upstream in the flow [1]. The jet is then induced at a frequency corresponding to the passage of vortical structures on top of the sensor. The adaptative control tries to improve the previous results by modification of the transfert function, based on statistical arguments [2]. Then, a control based on the physical interpretation of the vorticity creation near to the wall caused by a normal jet to the wall is considered. It uses several sensors and actuators [3]. Finally, the sub-optimal control allows to reach the objective by minimizing a functionnal with the use of an adjoint problem coming from the governing equations [4]. Each of these techniques gives satisfactory results. Moreover, several comparisons lead to very clear conclusions on what is essential -and what is not essential- to make the control efficient.

References:

[1] G. Hernandez, Controle actif des instabilites hydrodynamiques des ecoulements subsoniques compressibles , These CERFACS, France, 1996.

[2] B. Widrow and S.D. Stearn, Adaptive signal processing , Prentice-Hall, 1985.

[3] P. Koumoutsakos, Active control of vortex-wall interactions , Physics of fluids, 9 (12), pp 3808-3816, 1997.

[4] T. Bewley, H. Choi, R. Temam and P. Moin, Optimal feedback control of turbulent channel flow , Technical report annual research briefs, center for turbulence research, 1993.

We present an efficient adaptive technique for the numerical solution of partial differential equations of various type. Our aim is to generate a triangular grids with small number of elements where the satisfactory numerical solution can be achieved. We derive the mesh quality parameter and describe the algorithm how to optimize it. The main advantage of the anisotropic mesh adaptation is the independence of the used numerical scheme (finite difference, finite element, finite volume). The high efficiency is observed if the solutions contains some ,,singularities'', discontinuities, steep gradients. The generality of the method is demonstrated in problems of inviscid as well as viscous flow simulation and the thermoregulation of premature infants.

The paper is concerned with the use of the Discontinuous Galerkin Finite Element Methods for the solution of nonlinear convection-diffusion problems and compressible flow. The sought solution is approximated in space by piecewise linear discontinuous functions over convex polyhedra. The convective fluxes are approximated with the aid of the finite volume approach and the approximation of the diffusion terms is carried out by the method proposed by I. Babuska, E. Baumann and T. Oden. Time is considered either continuous (the method of lines) or a suitable Runge-Kutta discretization is used. An important problem is the limitingävoiding spurious oscillations in the numerical solution. We propose two new methods and analyze them theoretically, as well as with the aid of numerical experiments. The method is applied to the solution of high speed compressible flow.

The presented results were obtained in cooperation of the author with V. Dolejsi and C. Schwab. The research was supported under the grant No. 201/99/0267 of the Czech Grant Agency and grant No. MSM 113200007.

We consider Laplace equation in the domain with the large number of small absolutely conducting fillers. The solution takes the constant (not known) values on the fillers. Earlier proposed methods [1,2] deal with the equations with the continuous coefficients cannot be adopted to the such kind media.

Formulation of the problem.
Consider the domain in which the particles . Denote the remaining part of the domain by .

Consider the problem

The special finite elements for high-contrast dense packing system of particles.
The problem above is not the problem that can be soled using a uniform mesh. We can use a non-uniform mesh (mesh of variable density). For the high-contrast medium with dense packing particles it would not effective too. Explain this fact. Our theoretical analysis of the problem [3] predicts that the energy fluxes are concentrated in the necks between the neighbor particles. Thus the space outside the inclusions and the necks is equivalent to an empty space. Thus, computations (with both uniform or non-uniform mesh) involving this space will lead to computations ,,in empty space `` .

The problem can be solved by constructing suitable finite elements in the necks only. We construct such kind finite elements and arrive at a finite (,,net`` ) problem. The obtained ,,net ``problem is not only a formal finite approximation for the continuous problem, it has a physical interpretation.

Numerical computations.
We use the discrete network to compute the effective conductivity of high-contrast composite numerically. For this purpose we employ a computer program which generates a random distribution of disks on the plane. Using this distribution we obtain the corresponding discrete network. Furthermore the computer program provides the distribution of fluxes in the network which is based on the Keller's formula for two closely spaced disks. We compute the dependence of the effective conductivity on the volume fraction of the inclusions for monodispersed composites and obtained results which are consistent with the percolation theory predictions. The computer program which is based on our network model is very efficient and it allows us to collect the statistical data for a large number of random configurations.

References:

[1] Borcea, L., Papanicolaou G., Network approximation for transport properties of high contrast materials. SIAM J Appl Math, 58(2), (1998), 501-539.

[2] Kozlov, S.M., Geometrical aspects of averaging. Russ. Math. Surveys, 44:22, (1989), 91-144.

[3] Berlyand, L., et al Network Approximation in the Limit of Small Interparticle Distance of the Effective Properties of a High Contrast Random Dispersed Composite. Archive for Rational Mechanics and Analysis. (2001) in print

A singularly perturbed reaction-diffusion problem with homogeneous Dirichlet boundary condition is considered. It exhibits in general a solution with strong boundary and/or interior layers. This anisotropy is reflected in the discretization by using meshes with anisotropic elements.

Adaptive solution methods are based on a posteriori error estimators. The Equilibrated fluxes method and its modification for the singular perturbed case, done by Ainsworth and Oden, are discussed with respect to the application on anisotropic meshes. Further modifications of this error estimator for the anisotropic case are proposed.

The circulations in the ocean like the Gulf stream can be described with the shallow water equations. These pdes are discretizes with an Adams-Bashford scheme combined with the Crank-Nicholson scheme for the time derivatives and spectral elements for the discretization in space. The resulting coupled system of equations will be reduced to a Schur complement system with a special structure of the Schur complement. This system can be solved with a preconditioned conjugate gradients, where the matrix-vector product is only implicitly given. We derive an overlapping block preconditioner based on additive Schwarz methods for preconditioning the reduced system that takes into account the special structure of the elements used.

We present the a posteriori error analysis and adaptive mesh design for discontinuous Galerkin finite element approximations to systems of nonlinear hyperbolic conservation laws.

Shock capturing is used to reduce over-shoots at shocks. At curved boundaries we employ higher order boundary approximations to avoid non-physical entropy production at reflective boundaries.

We discuss the question of a posteriori error estimation for general linear and nonlinear functionals of the solution; typical examples include the outflow flux, local average and pointwise value, as well as the lift and drag coefficients of a body immersed in an inviscid fluid. By employing a duality argument, we derive so-called weighted a posteriori error bounds; in these error estimates the element-residuals are multiplied by local weights involving the solution of a certain dual problem. Based on these a posteriori bounds, we design and implement the corresponding adaptive algorithm to ensure efficient and reliable control of the error in the computed functional. The theoretical results are illustrated by a series of numerical experiments. In particular, we demonstrate the superiority of the proposed approach over standard mesh refinement algorithms which employ ad hoc error indicators.

References:

[1] W. Bangerth, R. Hartmann, and G. Kanschat: deal.II Differential Equations Analysis Library, Technical Reference. IWR, University of Heidelberg, Aug. 2001. Available from http://gaia.iwr.uni-heidelberg.de/ deal/.

[2] F. Bassi and S. Rebay: High-order accurate discontinuous finite element solution of the 2D Euler equations. J. Comput. Phys. 138:251-285, 1997.

[3] R. Hartmann: Adaptive FE-methods for conservation equations. In: G. Warnecke and H. Freistühler (Eds.) Proc. Eighth International Conference on Hyperbolic Problems. Theory, Numerics, Applications (HYP2000). Birkhäuser, Basel. (to appear).

[4] R. Hartmann and P. Houston: Adaptive Discontinuous Galerkin Finite Element Methods for Nonlinear Hyperbolic Conservation Laws. Preprint 2001-20 (SFB 359), IWR Heidelberg, Mai 2001, Submitted to SIAM J. Sci. Comp.

[5] J. Jaffre, C. Johnson, and A. Szepessy: Convergence of the discontinuous Galerkin finite element method for hyperbolic conservation laws. Math. Models and Methods in Appl. Sciences, 5:367-386, 1995.

The paper is concerned with Nitsche-type mortaring for treating weak continuity across non-matching meshes for domain decomposition according to the generalization (R. Stenberg, 1998) of some method of J. A. Nitsche (1971). The approach is applied to the Poisson equation with different types of boundary conditions. The interface of the domain decomposition may pass corners of the domain or touch collision points of boundary conditions of different type where the solution has in general singular behaviour. Moreover, the approach is extended to Poisson-like problems with discontinuous coefficients and polygonal interfaces connected with singularities (joint work with S. Nicaise, 2001). For such problems and non-matching meshes of triangles with local refinement near the corners of the boundary or interface, some properties of the finite element schemes and error estimates in a -like norm and in the -norm are proved. They show that appropriate mesh grading at the interface of non-matching grids yields convergence rates as known for the classical finite-element method in presence of regular solutions. Numerical examples illustrate the approach and confirm the theoretical results.

This talk presents the framework of hierarchical hybrid grids, which were introduced in order to combine the flexibility of unstructured grids with the high performance of structured ones. Hierarchical hybrid grids employ several grid levels which serve different purposes. The coarse and in general unstructured levels represent the geometry and the topology. The computations are carried out on highly structured refinements of the coarse grid elements. The talk discusses the main concepts and demonstrates the performance gain for simple iterative schemes for linear algebraic systems. The experimental results from several computer platforms, ranging from workstations to supercomputers, underline the performance potential of the approach.

In this paper we consider the adaptive finite element solution of a general class of variational problems using a combination of node insertion, node movement and edge swapping. The adaptive strategy that is proposed is based upon the construction of a hierarchy of locally optimal meshes starting with a coarse grid for which the location and connectivity of the nodes is optimized. This grid is then locally refined and the new mesh is optimized in the same manner. Results will be presented both for triangular meshes in two dimensions and tetrahedral meshes in three dimensions. This is joint work with Rashid Mahmood.

We consider a general framework for analysing the convergence of multi-grid solvers applied to finite element discretisations of mixed problems, both of conforming and nonconforming type. As a basic new feature, our approach allows to use different finite element discretisations on each level of the multi-grid hierarchy. Thus, in our multi-level approach, accurate higher order finite element discretisations can be combined with fast multi-level solvers based on lower order (nonconforming) finite element discretisations. This leads to the design of efficient multi-level solvers for higher order finite element discretisations.

The efficiency of this multiple discretization multigrid approach is demonstrated in the solution of the 3D Navier-Stokes equations.

References:

[1] V. John, P. Knobloch, G. Matthies, L. Tobiska, ,,Non-nested multi-level solvers for finite element discretizations of mixed problems`` Preprint 11/2001, Fakultät für Mathematik, Otto-von-Guericke-Universität Magdeburg

[2] V. John, G. Matthies, L. Tobiska, ,,On higher order finite element discretizations for the incompressible Navier-Stokes equations in three dimensions`` , Preprint 06/2001, Fakultät für Mathematik, Otto-von-Guericke-Universität Magdeburg

A mixed discontinuous finite element method for elliptic problems called the local discontinuous Galerkin method will be presented. This method will be extended to Stokes and linearized Navier-Stokes equations. It will be shown, that it is possible to solve the arising linear algebraic systems efficiently, using a multi-level preconditioner.

References:

[1] Bernardo Cockburn, Guido Kanschat, Dominik Schötzau, and Christoph Schwab: Local discontinuous Galerkin methods for the Stokes system. http://www.ima.umn.edu/preprints/oct2000/oct2000.html, IMA Preprint 1728, SIAM J. Numer. Anal., to appear

[2] J. Gopalakrishnan and G. Kanschat: A multilevel discontinuous Galerkin method. http://www.ima.umn.edu/preprints/dec2000/dec2000.html, IMA Preprint 1735, Numer. Math., to appear

email: agk_at_neic.nsk.su

Considering a plate of priodic structure (e.g. ribbed plate), we describe it with the so called homogenenized (called also overall, effective) stiffnesses, which describes the plate as a two-dimensional object. Thus, considering a plate of periodic structure, we must first computer its homogenized stiffnesses. The homogenization method establishes a rigor relationship between the local (called also microscopic) and the homogenized (called also macroscopic or effective) characteristics of composites. The homogenization procedures are known today for the basis types of structural members: solid composites [Bensoussan, Lions, Papanicolaou (1978); Sanchez-Palencia (1980); Bakhvalov,Panasenko (1989)], composite plates, and composite beams [Kalamkarov and Kolpakov (1997)]. It is known that the homogenized procedure is related with variational principles.

For the solid composites numerous contributors paid attention to deriving variational principles for the homogenized characteristics of composite both on the basis of the homogenization method and using other approaches [Milton (1990); Milton, Kohn (1988); Francfort, Murat (1986)] (the list of references is not completed). To the knowledge of the author the analogous problems were not considered for the plates and beams (except the papres [Kolpakov (1998,1999)] which are the basis for this presentation).

A composite plate, for the case when characteristic dimension of inhomogeneties is small in compare with dimensional of the plate, can be approximated with a homogeneous plate model. The stiffnesses of the corresponding homogeneous plate are called the homogenized stiffnesses (in-plane, coupling and bending).

In the paper variational principles for the stiffnesses are derived. The variational principles are applied to derivation of two-side estimates for the stiffnesses. In particular, the plate analogs of Voight and Reuss estimates [Voight (1928); Reuss (1929)] were derived. The variational principles allow us to derive the correspondent finite-elements problem. Making the finite-element approximation of the variational principles, we can derive a finite-dimentional problem for computation of the stiffnesses. The advantage of this method is that we computer the stiffnesses in a ,,direct way`` without solution of a intermediate problem, as usually it is done.

References:

[1] Bakhvalov N.S., Panasenko G.P. (1989) Homogenization: Averaging processes in periodic media. Kluwer.

[2] Bensoussan A., Lions J-L., Papanicolaou G. (1978) Asymptotic analysis for periodic structures. North-Holland Publ.Comp,.

[3] Francfort G.A., Murat F. (1986) Homogenization and optimal bonds in linear elasticity. Arch.Rat.Mech. and Analysis. V.94.

[4] Sanchez-Palencia E. (1980) Non-homogeneous media and vibration theory. Springer. Berlin.

[5] Kalamkarov A.L., Kolpakov A.G. (1997) Analysis, design and optimization of composite structures. J.Wiley and Sons.

[6] Kolpakov A.G.(1998) Variational principles for stiffnesses of a non- homogeneous beam J. Mech. Phys. Solids, V.46, N 6.

[7] Kolpakov A.G. (1999).Variational principles for stiffnesses of a non- homogeneous plate. J. Mech. Phys. Solids (in print).

[8] Milton G.W. (1990) On characterizing the set of possible effective tensors for composite: the variational method and translation method. Comm. Pure Appl.Math. V.43.

[9] Milton G.W., Kohn R. (1988) Variational bounds on the effective moduli of anisotropic composites. J .Mech. Phys. Solids. V.36.

[10] Reuss A. (1929) Berechnung der fliessgrenze von mischkristallen auf crund der platiztatsbedingung fur einkristalle. ZAMM. V.9. 49.

[11] Voight W. (1928) Lehrbuch der Kristallphysik. Teubner. Berlin. 1928.

####################################################################### -->

We consider a posteriori error estimators that can be applied to anisotropic tetrahedral finite element meshes, i.e. meshes where the aspect ratio of the elements can be arbitrarily large. Two kinds of Zienkiewicz-Zhu (ZZ) type error estimators are derived which are both based on some recovered gradient. Two different, rigorous analytical approaches yield the equivalence of both ZZ error estimators to a known residual error estimator. Thus reliability and efficiency of the ZZ error estimation is obtained. Particular attention is paid to the requirements on the anisotropic mesh. The analysis is complemented and confirmed by several numerical examples.

In the hp-version of the finite element method (hp-FEM), convergence can be achieved either through mesh refinement or by increasing the approximation order. We present an hp-adaptive algorithm where the decision whether to perform h-refinement or p-enrichment is based on the local convergence history. The algorithm is based on local residual-based error indicators. Reliability of the error estimator is proved; the efficiency constant of the error estimator is O(p). The work presented is joint with B. Wohlmuth.

Let us consider the Laplace equation or the Stokes system in a three-dimensional bounded domain with Dirichlet boundary conditions. If is smooth, then the solutions of these equations are smooth [11,12], while if is a polyhedral domain, then the solutions have in general singularities near the corners and the edges of [6,7,3,4]. Consequently if is not convex, classical mixed finite element methods [16,17,10] on quasi-uniform meshes have a slow convergence rate.

For two-dimensional domains with corner singularities, the use of refined meshes in a neighbourhood of the singular corners allows to restore the optimal order of convergence [8,9]. Our goal is then to extend the mesh refinement method in three-dimensional polyhedral domains in order to obtain an optimal order of convergence. For standard finite element method for the Laplace equation, it has been shown that anisotropic mesh grading (in the sense that elements in the refined region have an aspect ratio which grows to infinity as h -> 0 , h being the global meshsize of the triangulation) is appropriate to compensate this effect and to obtain the optimal order of convergence [5,13]. In [2,3,4] prismatic domains were considered. This restriction was made there because the authors wanted to focus on edge singularities, and such domains do not introduce additional corner singularities. The finite element meshes were graded perpendicularly to the edge and were quasi-uniform in the edge direction. In our work, we extend these last results to some mixed FEM for the Laplace equation and the Stokes system using some J.-C. Nédélec elements [14] in the case of prismatic triangulations and Raviart-Thomas elements [16,17,10] in the case of tetrahedral triangulations. The background is anisotropic regularity results for the solutions of the Laplace equation and the Stokes system on such prismatic domains obtained in [3,4]. The main point is to derive anisotropic local interpolation error estimates for functions from anisotropic weighted Sobolev spaces in the spirit of [1,4,15].

The outline of my lecture will be the following one: Firstly, I shall describe two families of anisotropically graded finite element meshes based on prismatic elements and tetrahedral elements respectively which turned out to be suited for the treatment of edge singularities [2,3,4]. I shall further introduce the J.-C. Nédélec finite element spaces [14] and Raviart-Thomas finite element spaces [16,17] and show that the associated interpolant operators are well-defined for functions in appropriate anisotropic weighted Sobolev spaces.

As usual our error analysis requires some local interpolation error estimates, which are investigated for prismatic elements and tetrahedral elements respectively. Note that for tetrahedral elements, contrary to the habit, we use a composition of interpolation operators in order to avoid a geometrical obstacle [1].

Then I shall consider the mixed FEM of the Laplace equation. Using anisotropic regularity results from [3] and our previously obtained global interpolation error estimates for prismatic and tetrahedral triangulations, I shall show that appropriate refined meshes lead to the optimal finite element error estimate:

Finally, in the last part of my talk, I shall show that a similar analysis holds for the Stokes problem with Dirichlet boundary condition in which the gradient of the velocity field is introduced as a supplementary unknown using the regularity results from [4] and our previous interpolation error estimates.

References:

[1] G. Acosta and R. G. Durán, The maximum angle condition for mixed and non-conforming elements, application to the Stokes equations, SIAM J. Num. Analysis, 37, 1999, 18-36.

[2] Th. Apel and M. Dobrowolski, Anisotropic interpolation with applications to the finite element method, Computing, 47, 1992, 277-293.

[3] Th. Apel and S. Nicaise, Elliptic problems in domains with edges: anisotropic regularity and anisotropic finite element meshes, in J. Céa, D. Chenais, G. Geymonat, and J. L. Lions editors, Partial Differential Equations and Functional Analysis (In Memory of Pierre Grisvard), 18-34, Birkhäuser, Boston, 1996.

[4] Th. Apel, S. Nicaise, and J. Schöberl, A non-conforming FEM with anisotropic mesh grading for the Stokes problem in domains with edges, I.M.A. J. Numerical Analysis, to appear.

[5] Th. Apel, A.-M. Sändig, J.R. Whiteman, Graded mesh refinement and error estimates for finite element solutions of elliptic boundary value problems in non-smooth domains, Math. Methods Appl. Sci., 19, 63-85, 1996.

[6] M. Dauge, Elliptic boundary value problems on corner domains, Lect. Notes in Mathematics, 1341, Springer, Berlin, 1988.

[7] M. Dauge, Stationary Stokes and Navier-Stokes systems on two- or three-dimensional domains with corners I, SIAM J. Math. Anal., 20, 1989, 74-97.

[8] H. El Sossa and L. Paquet, Refined mixed finite element method of the Dirichlet problem for the Laplace equation in a polygonal domain, Rapport de Recherche 00-5, Laboratoire MACS, Université de Valenciennes, France, submitted to Adv. Math. Sc. Appl.

[9] H. El Sossa and L. Paquet, Méthodes d'éléments finis mixtes raffinés pour le problème de Stokes, Rapport de Recherche 01-1, Laboratoire MACS, Université de Valenciennes, France,

[10] M. Farhloul, Mixed and nonconforming finite element methods for the Stokes problem, Can. Appl. Math. Quart., 3, 1995, 399-418.

[11] V. Girault and P.-A. Raviart, Finite element methods for Navier-Stokes equations, Springer Series in Comp. Math. 5, Springer-Verlag, 1986.

[12] P. Grisvard, Elliptic problems in nonsmooth domains, Monographs and Studies in Mathematics 24, Pitman, Boston, 1985.

[13] J. Lubuma and S. Nicaise, Dirichlet problems in polyhedral domains II: Approximation by FEM and BEM, J. Comp. Appl. Math., 61, 1995, 13-27.

[14] J.-C. Nédélec, A new family of mixed finite elements in , Numer. Math., 50, 1986, 57-81.

[15] S. Nicaise, Edge elements on anisotropic meshes and approximation of the Maxwell equations, submitted to SIAM Journal on Numerical Analysis.

[16] P. A. Raviart and J. M. Thomas, A mixed finite element method for second order elliptic problems, in I. Galligani and E. Magenes eds., Mathematical aspects of Finite Element Methods, Lecture Notes in Mathematics 606, Springer-Verlag, 1977, 292-315.

[17] J. E. Roberts and J. M. Thomas, Mixed and hybrid Methods, in J. L. Lions and P. G. Ciarlet eds, Handbook of Numerical Analysis, Vol. II, Finite Element Methods (Part 1), North-Holland, Amsterdam, 1991, 523-639.

The development of accurate and efficient element formulations for thin-walled structures has been in the focus of research in computational mechanics since the event of the finite element method. It seemed to be clear very early, that an investigation of plate or shell problems with tetrahedral or hexahedral elements is not feasible for practical problems, as a sufficient accuracy could only be obtained by a prohibitively large amount of degrees of freedom and computational effort. The major reasons for this observation are the mapping requirements of isoparametric, low order elements. Accurate solutions can only be obtained, if the aspect ratio of an element is close to one, resulting in an enormous amount of elements, even if only a few layers are used over the thickness of the structure. A very natural consequence of this observation was to use dimensionally reduced models like Reissner-Mindlin plates or Naghdi shells, and to build element formulations on top of these theories. Yet, it turned out that naive displacement type elements for these models lead to notorious numerical problems like locking or spurious energy modes, giving rise to the development of numerous improvements, like mixed elements or enhanced strain formulations. Although many of these 'tricks' have shown to be very successful in practice and are now well understood from a mathematical point of view, they are often connected with 'crimes' being sometimes of pure mathematical nature, but often also due to a violation of the underlying model assumptions, like the kinematics of the displacement field over the thickness of the structure.

As an alternative to these well-known and widely used dimensionally reduced formulations we will investigate in this paper the feasibility of strictly three-dimensional models, using high order elements being coupled to a precise geometric description of the structure. As a key issue the p-version of the FEA is used, offering a consistent and accurate way to implement solid elements having a very large aspect ratio (up to a few hundred) and to represent much more general shapes of element surfaces than those available in the usual isoparametric approach. A transition from thin- to thick-walled constructions is thus possible without the necessity to couple models of differing dimensions and without imposing any restrictions on the (three-dimensional) kinematics of the structure. We will focus our discussion especially on the question of an efficient implementation of these elements, i.e. on an advantageous choice of anisotropic higher order ansatz spaces, on coupling of the finite element analysis to a geometric model and on an adaptive integration technique for higher order elements. Using these 'tricks' which are often not known or not necessary for low order elements, one obtains an efficient code being consistent to the three-dimensional theory of elasticity by construction. We will demonstrate our results and compare them with respect to accuracy and computational effort to dimensionally reduced models in several numerical examples.

References:

[1] A. Düster, H. Bröker, E. Rank ``The p-Version of the Finite Element Method for three-dimensional curved thin walled structures'', submitted to International Journal for Numerical Methods in Engineering, (2000).

In this talk we present a general approach to algebraic multigrid methods for problems arising from the finite element discretization of a second order, self-adjoint, elliptic partial differential equation. Special attention is paid to the coarsening process and the transfer operators. In order to construct a flexible method an auxiliary matrix is introduced which represents a virtual finite element mesh. In addition this auxiliary matrix is related to the degrees of freedom of the system matrix. The coarsening is performed on the auxiliary matrix, and after defining appropriate transfer operators for the system and the auxiliary matrix, a coarse system is constructed by Galerkin's method.

In order to get additional speed up we propose a parallelization of the algebraic multigrid algorithm. The realization is based on domain decomposition ideas which is well suited for distributed memory computers.

Finally we present some numerical studies on parallel computers with distributed memory which show the high efficiency of the approach.

References:

[1] G. Haase, M. Kuhn, S. Reitzinger: Parallel Algebraic Multigrid Methods on Distributed Memory Computers. SFB Preprint 00-16, University of Linz, 2000. Submitted to SIAM Journal on Scientific Computing.

[2] G. Haase, U. Langer, S. Reitzinger, J. Schöberl: A General Approach to Algebraic Multigrid Methods. SFB Preprint 00-33, University of Linz, 2000.

[3] S. Reitzinger: Algebraic Multigrid Methods for Large Scale Finite Element Equations. PhD Theses, University of Linz, 2001.

It is an open problem to prove optimal uniform convergence results for linear convection dominated convection-diffusion equations if parabolic boundary layers exist. Based on a new decomposition of the solution we are able to present such a result for bilinear finite elements on layer adapted meshes.

Electrically conducting fluid flow in which the electromagnetic forces can be of the same order or even greater than the hydrodynamic ones is often modelled by the equation of magnetohydrodynamics (MHD). The ideal MHD equations consists of the following set of nonlinear hyperbolic equations

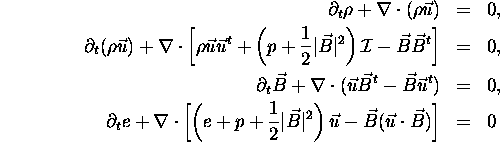
together with the additional divergence constraint

Here denotes the magnetic induction, the fluid velocity, the density and e the energy density.

To obtain numerical solutions for such systems of conservation laws on unstructured grids one often uses finite volume schemes of first and second order. Doing this, the exact solution is approximated by piecewise constant values on each cell of the grid; using linear reconstruction and Runge-Kutta timestepping, these schemes can formally be extended to second order.

We have implemented and tested a Discontinuous Galerkin method for the MHD equations. In this scheme the numerical solution is approximated by polynomials of higher order on each cell of the grid. The main focus of interest is the comparison of the Discontinuous Galerkin method and the finite volume schemes of higher order with respect to measured errors, convergence rates and computational time as well as the question, whether the use of polynomials of grad 2 might yield better error to runtime ratios in the case of discontinuous solutions.

References:

[1] B. Cockburn: Discontinuous Galerkin methods for convection-dominated problems, Higher-Order Methods for Computational Physics (T. Barth and H. Deconink, eds.), Lecture Notes in Computational Science and Engineering, vol. 9, Springer Verlag, 1999, pp. 69-224.

[2] J. Becker: Entwicklung eines effizienten Verfahrens zur Lösung hyperbolischer Differentialgleichungen, Universität Freiburg, Dissertation 1999

Reliable and efficient residual-based a posteriori error estimates are established for the stabilised locking-free finite element methods for the Reissner-Mindlin plate model. The error is estimated by a computable error estimator from above and below up to multiplicative constants that do neither depend on the mesh-size nor on the plate's thickness and are uniform for a wide range of stabilisation parameter. The error is controlled in norms that are known to converge to zero in a quasi-optimal way.

References:

[1] C. Carstensen, J. Schöberl: Residual-Based A Posteriori Error Estimate for a Mixed Reissner-Mindlin Plate Finite Element Method. SFB-Report No. 00-31, Johannes Kepler Universität Linz, SFBF013, Linz, Austria

Finite element discretization and linearization of the incompressible Navier-Stokes equations leads to linear algebraic systems with the saddle-point structure:

 

References:

[1] Silvester, D., Elman, H., Kay, D. and Wathen, A., 2001. Efficient preconditioning of the linearised Navier-Stokes equations for incompressible flow, J. Computational and Applied Mathematics (special millennium issue vol. 7), 128, pp. 261-279.

[2] Elman, H., Silvester, D. and Wathen, A., 2001. Performance and analysis of saddle point preconditioners for the discrete Navier-Stokes equations, Numerische Mathematik, to appear.

In this talk we discuss the coupling of a mixed finite element method and a symmetric boundary element method for the Stokes problem. The coupling is formulated in terms of local Steklov-Poincaré operators defined by the solution of local Dirichlet problems. For the boundary element method we use piecewise linear trial functions to approximate the velocity on the boundary while for a stable finite element discretization we use Taylor-Hood elements within the interior of the finite element subdomain. Note that the unknown velocity on the coupling boundary is approximated by piecewise linear basis functions only. To define the Steklov-Poincaré operator via boundary integral operators we need to have the invertibility of the single layer potential. Due to the non-uniqueness of the pressure we obtain a non-trivial kernel whose dimension depends on the topology of the domain. Hence we introduce an extended boundary integral equation for the single layer potential. Then we can prove the unique solvability of the coupled variational formulation and we can derive standard error estimates for the Galerkin approximation.

References:

[1] B. Reidinger, O. Steinbach, A symmetric boundary element method for the Stokes problem in multiple connected domains. In preparation.

We present several families of locking free finite element methods for the Reissner-Mindlin plate model.

First, we modify a formulation of Hughes and Franca to a new method in which the displacement and rotation are only unknowns. The formulation is stable independent of the choice of basis functions, no Babuska-Brezzi condition have to be satisfied. For an optimal convergence rate (in the thin limit) the displacement has, however, to be on one degree higher than the rotation.

Next, we show that a method with equal order interpolation is obtained when combining it with the MITC covariant interpolation of the shear strain.

We give the results of benchmark computations with the methods. It is also shown that the stabilization has very good effect on preconditioned conjugate gradient and multigrid methods for solving the discrete linear system.

This talk starts from an orthogonal decomposition of the Sobolev space of vector functions (defined on a Lipschitz domain , d=2,3). The decomposition has been discovered by Crouzeix in 1974, and, independently, by Velte in 1990, and has connections to the inf-sup stability condition of the Stokes boundary value problem as well as to the Korn inequality.

A corresponding decomposition can be introduced purely algebraically or after discretization using the staggered grid difference approximation or, in two dimensions, the Scott-Vogelius finite elements. In this way one obtains information about the spektrum of the discrete Stokes-Schur complement operator which is useful for accelerating iterative methods for the solution of the Stokes problem.

Moreover, it becomes visible that a purely algebraic vector analysis can be built with vectors and matrices instead of vector functions and operators, including algebraic Cauchy-Riemann equations and an algebraic Helmholtz decomposition.

This approach leads to a better understanding not only of numerical methods for the discretized Stokes problem but also of the analytical case.

References:

[1] G. Stoyan, = -grad div + rot rot for matrices, with application to the finite element solution of the Stokes problem. East-West Journal of Numerical Mathematics, 8,4 (2000), 323-340.

Taylor-Hood elements are a suitable discretization for mixed problems with conforming piecewise quadratic approximations for the primal variable and conforming piecewise linear approximations for the dual variable. We show that Taylor-Hood elements can be constructed for 3D adaptive meshes including hexahedra, prisms, pyramids, and tetrahedra. The stability of Taylor-Hood elements on hexahedra, prisms, and pyramids is proved by reviewing Verfürth's proof for tetrahedra.

In the first application, we consider nearly incompressible elasticity. We present examples implemented in the software system UG, where the resulting linear systems are solved with an adaptive multigrid method. The performance of Taylor-Hood elements with continuous pressure approximation is compared with elements, where the pressure approximation is discontinuous.

In the second application, we consider a viscoplastic hybrid two phase model in soil mechanics: find displacements and pressure with boundary conditions for and for and find plastic strains , satisfying the equations

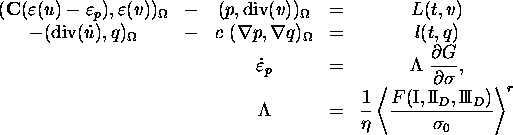
A Galerkin finite element method that uses piecewise linear functions on Shishkin- and Bakhvalov-Shishkin-type of meshes is applied to a linear reaction-diffusion equation with discontinuous source term. The method is shown to be convergent, uniformly in the perturbation parameter, of order for the Shishkin-type mesh and for the Bakhvalov-Shishkin-type mesh, where N is the mesh size number. Numerical experiments support our theoretical results.

References:

[1] P.A. Farrell, J.J.H. Miller, E. O'Riordan, G.I. Shishkin: Singularly perturbed differential equations with discontinuous source terms, to appear

[2] H.-G. Roos, T. Lin: Sufficient conditions for uniform convergence on layer-adapted grids, Computing 63 (1999) 27-45