Solitons are nonlinear waves. As a preliminary definition,
a soliton is considered as solitary, traveling wave pulse solution
of nonlinear partial differential equation (PDE). The nonlinearity
will play a significant role. For most dispersive evolution equations
these solitary waves would scatter inelastically and lose 'energy' due
to the radiation. Not so for the solitons: after a fully nonlinear interaction,
the solitary waves remerge, retaining their identities with same speed
and shape.
It should have remarkable stability properties. Stability plays
a important role in soliton physics.
The beginning of soliton physics in often dated back to the month of
August 1834 when John Scott Russell observed the ``great wave of
translation''. He describes what he saw in [1]:
-
"I believe I shall best introduce this phenomenon by describing the circumstances of my own first acquaintance with it. I was observing the motion of a boat which was rapidly along a narrow channel by a pair of hoses, when the boat suddenly stopped-not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation; then suddenly leaving it behind, rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well defined heap of water, which continued its course along the channel apparently without change of form or dimension of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to foot and half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon which I have called the Wave of Translation a name which it now very generally bears."
Due to the work of Stokes, Boussinesq, Rayleigh, Korteweg, de Vries, and
many others we know that the ``great wave of translation'' is a special
form of a surface water wave.
The equation describing the (unidirectional) propagation of waves on the
surface of a shallow channel was derived by Korteweg and de Vries in
1895. After performing a Galilean and variety of scaling transformations,
the KdV equation can be written in simplified form:
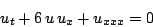
One soliton solution of this nonlinear PDE:
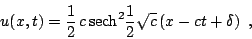
where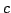 
is the speed of the soliton and 
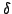is the phase. This clearly represents the solitary wave observed
by John Scott Russell and shows that the peak amplitude is exactely half the
speed. Thus larger solitary waves have greater speeds. This suggest a numerical
experiment: we start with two solitary wave solutions, with centers well
separeted and different amplitude.
Figure:
|
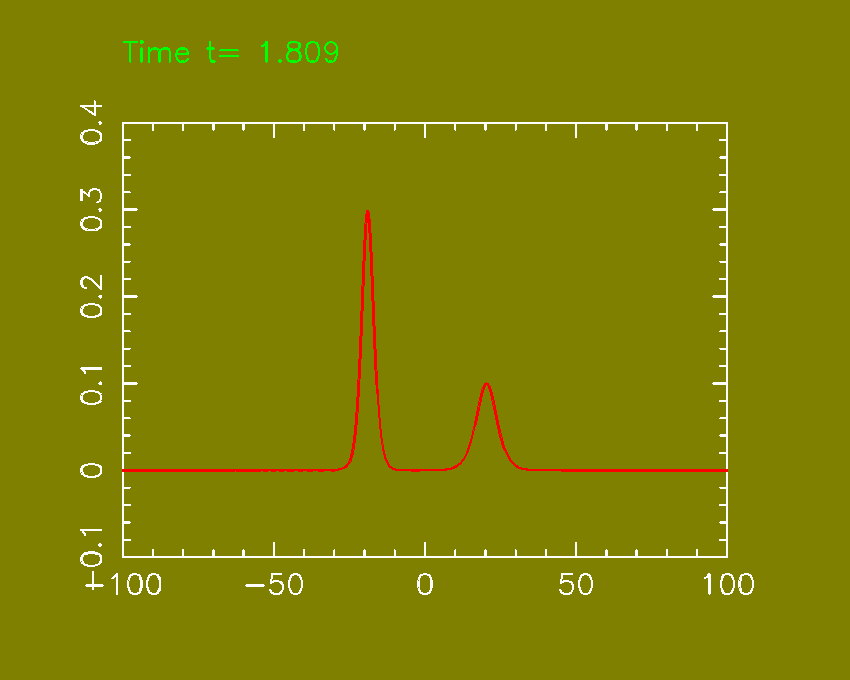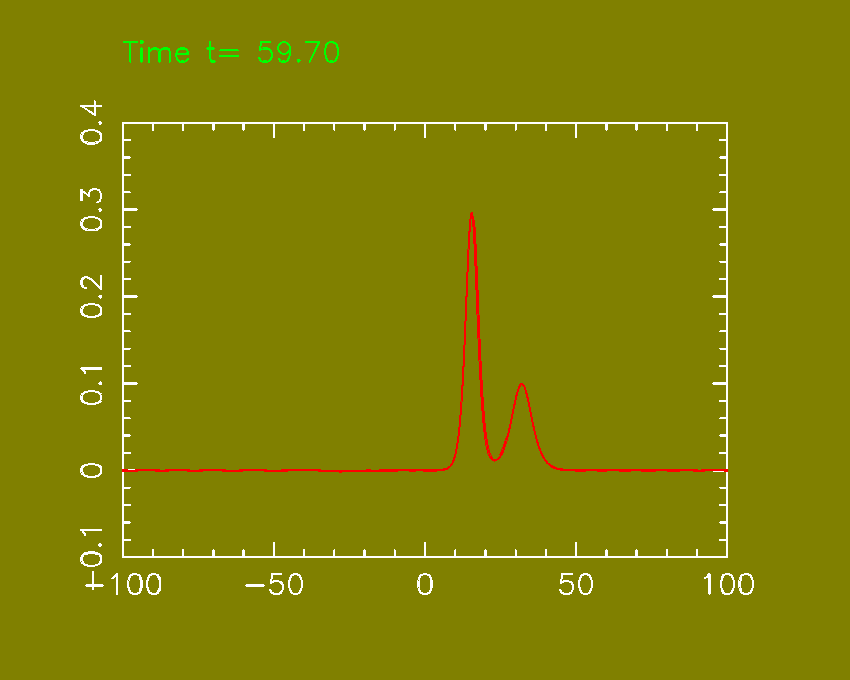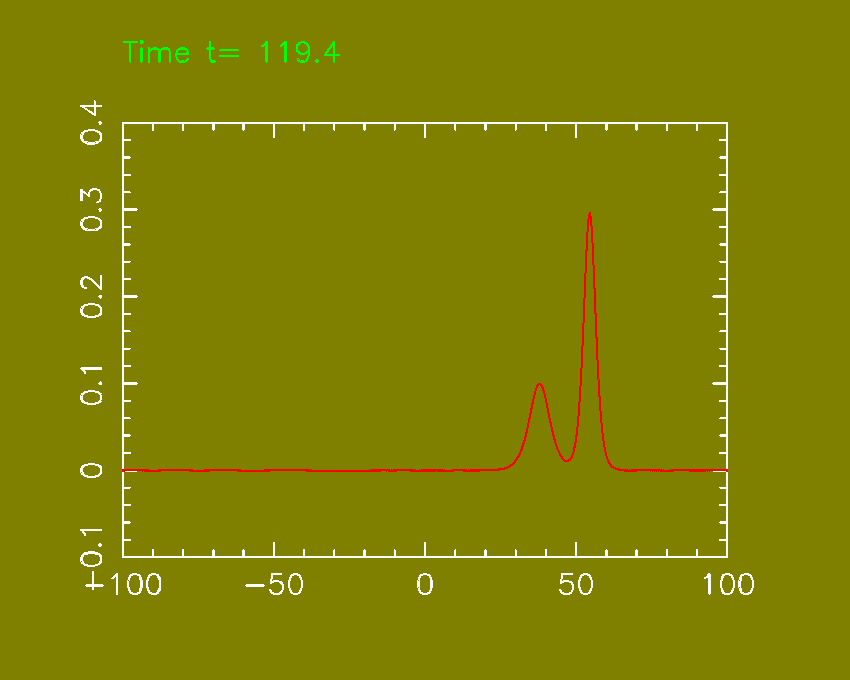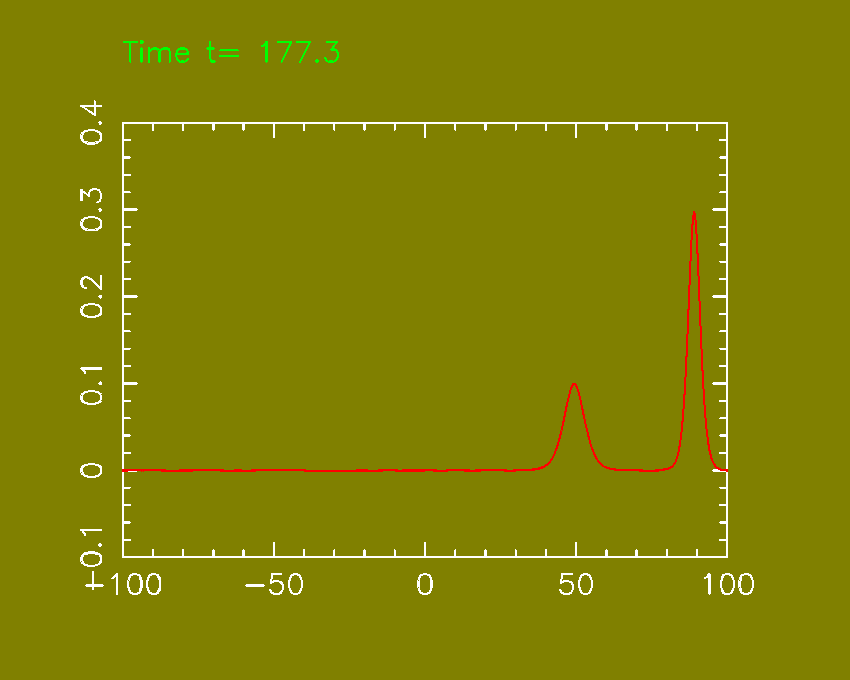
The KdV equation can admits also a Multi-soliton solution.
[1] J. Scott Russell. Report on waves, Fourteenth meeting of the British Association for the Advancement of Science, 1844.