Computeralgebra mit SymPy
Contents
6. Computeralgebra mit SymPy¶
In diesem Abschnitt wollen wir das Python-Modul SymPy vorstellen, welches uns ermöglicht symbolische Berechnungen durchzuführen. Insbesondere werden wir lernen, wie wir mit mathematischen Ausdrücken arbeiten können, wie wir Funktionen differenzieren und integrieren, und wie wir (nicht)lineare Gleichungssysteme und Differentialgleichungen lösen.
Wir müssen zunächst das Paket installieren, beispielsweise über unsere conda-Umgebung
conda install -c conda-forge sympy
und anschließend in unser Python-Skript einbinden:
import sympy as sy
6.1. Arbeiten mit Funktionen¶
Beginnen wir zunächst damit eine mathematische Funktion zu definieren. Dazu müssen wir die veränderliche Variable kennzeichnen und anschließend die Funktionsvorschrift eingeben:
x = sy.symbols('x')
f = 1./3*x**3 - 2.*x**2 + 3.
Die Variable x ist vom Typ
type(x)
sympy.core.symbol.Symbol
und der Ausdruck f vom Typ
type(f)
sympy.core.add.Add
Objekte vom Typ sympy.core.add.Add entstehen bei der Summation von, in unserem Fall
len(f.args)
3
symbolischen Ausdrücken, welche wiederrum aus anderen Rechenoperationen hervorgegangen sind:
g1 = f.args[0]
print("Erster Summand", g1, "vom Typ", type(g1))
Erster Summand 3.00000000000000 vom Typ <class 'sympy.core.numbers.Float'>
g2 = f.args[1]
print("Zweiter Summand", g2, "vom Typ", type(g2))
Zweiter Summand 0.333333333333333*x**3 vom Typ <class 'sympy.core.mul.Mul'>
g3 = f.args[2]
print("Dritter Summand", g3, "vom Typ", type(g3))
Dritter Summand -2.0*x**2 vom Typ <class 'sympy.core.mul.Mul'>
Der Ausdruck g1 ist nur die Zahl 3.0 und g2 und g3 sind vom Typ sympy.core.mul.Mult, sind also Ausdrücke die aus der Multiplikation weiterer Ausdrücke hervorgegangen sind. Ein mathematischer Ausdruck wird schließlich in Form eines Binärbaums dargestellt. Die genaue Darstellung bekommen wir wie folgt:
sy.srepr(f)
"Add(Mul(Float('0.33333333333333331', precision=53), Pow(Symbol('x'), Integer(3))), Mul(Integer(-1), Float('2.0', precision=53), Pow(Symbol('x'), Integer(2))), Float('3.0', precision=53))"
Vielleicht haben wir durch diese Betrachtung schon eine grobe Vorstellung wie symbolische Ausdrücke funktionieren. Über die genauen Details wollen wir uns aber hier keine weiteren Gedanken machen.
Schauen wir uns an, was wir mit der eben definierten Funktion anstellen können
6.1.1. Differenzieren¶
Df = f.diff(x)
print("Ableitung:")
Df
Ableitung:
bzw. mit der freien Funktion sympy.diff
Df = sy.diff(f,x)
print("Ableitung:")
Df
Ableitung:
Natürlich kann SymPy auch kompliziertere Funktionen ableiten. Zu beachten ist hier, dass wir für alle mathematischen Funktionen die entsprechenden Funktionen aus dem SymPy-Modul verwenden:
g = sy.exp(-x**2)*sy.sin(x)
g.diff(x)
6.1.2. Integration¶
Mit der Methode integrate können wir die Stammfunktion einer Funktion berechnen lassen
F = f.integrate(x)
print("Stammfunktion:")
F
Stammfunktion:
Manchmal ist aber auch SymPy überfordert. Bei zu komplizierten Funktionen gibt die integrate-Methode lediglich
G = g.integrate(x)
print("Stammfunktion:")
G
Stammfunktion:
zurück. Wir können auch bestimmte Integrale berechnen, indem wir als zweiten Parameter ein Tupel bestehend aus der Integrationsvariablen und den beiden Grenzen angeben:
v = sy.integrate(f, (x,0,1))
print("Integral über f mit Grenzen 0 und 1:")
v
Integral über f mit Grenzen 0 und 1:
Um uneigentliche Integrale, beispielsweise \(\int_0^\infty g(x)\,\mathrm dx\) zu berechnen nutzt man als obere Grenze einfach sy.oo (unendlich):
g = x**2*sy.exp(-x)
v = sy.integrate(g,(x,0,sy.oo))
print("Uneigentliches Inegral:")
v
Uneigentliches Inegral:
6.1.3. Potenzreihen¶
SymPy bietet viele weitere nützliche Funktionen, beispielsweise sympy.series(...). Diese Funktion berechnet eine Potenzreihe beliebiger Ordnung für eine gegebene Funktion:
G = g.series(x, 0, 4) # Taylorapproximation im Entwicklungsunkt 0, bis Ordnung 4
print("Potenzreihe:")
G
Potenzreihe:
G = G.removeO()
print("Potenzreihe ohne Restglied:")
G
Potenzreihe ohne Restglied:
6.1.4. Plotten¶
SymPy stellt auch ein direktes Interface zu MatplotLib bereit. Der Unterschied zu den in Visualisierung mit Matplotlib gelernten Funktionen ist, dass wir hier nicht erst ein Gitter für die x-Werte anlegen müssen. Dies geschieht in den plot-Funktionen von SymPy automatisch. Wir müssen lediglich die SymPy-Expression und gegebenenfalls zusätzliche Funktionsparameter der sympy.plot-Funktion übergeben:
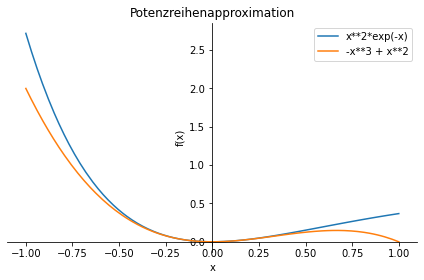
p1 = sy.plot(g, (x,-1,1), show=False, legend=True, title="Potenzreihenapproximation")
p2 = sy.plot(G, (x,-1,1), show=False)
p1.append(p2[0])
p1.show()
Übungsaufgabe
Berechne die Ableitung, die Stammfunktion, und erstelle einen Plot der Funktionen
6.2. Nichtlineare Gleichungen¶
Mit SymPy können wir auch nichtlineare Gleichungen bzw. Gleichungssysteme lösen. Dies geschieht algebraisch, sofern möglich.
Die Funktionen, welche wir dafür benötigen, ist sympy.solve(...). Wir konstruieren ein einfaches Beispiel in dem wir die stationären Punkte der Funktion \(f(x)=x\,\ln(x)\) berechnen:
f = x/(x**2+1)
Df = f.diff()
p3 = sy.plot(f,(x,-4,4)) # Plot function
eq = sy.Eq(Df, 0) # Create equation with lhs DF and rhs 0
sols = sy.solve(eq, x) # Solve the equation
print("Extrema at", sols) # Print solution
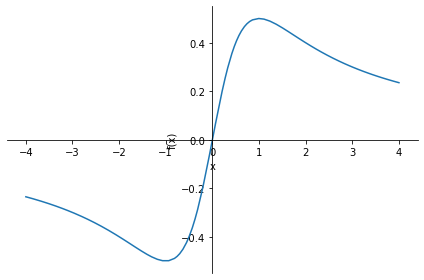
Extrema at [-1, 1]
Die stationären Punkte werden in einer Liste abgelegt. Über diese können wir anschließend iterieren. So wie in folgender Probe:
for sol in sols:
print("Stationärer Punkt x =", sol)
print("Ist vom Typ", type(sol))
print("Erfüllt f'(x) =", Df.subs(x, sol))
Stationärer Punkt x = -1
Ist vom Typ <class 'sympy.core.numbers.NegativeOne'>
Erfüllt f'(x) = 0
Stationärer Punkt x = 1
Ist vom Typ <class 'sympy.core.numbers.One'>
Erfüllt f'(x) = 0
Auch Systeme von Gleichungen können mit diesem Befehl gelöst werden wie folgendes Beispiel zeigt:
x1, x2 = sy.symbols("x1 x2")
equations = [
sy.Eq(2*x1 + 1*x2, 10),
sy.Eq(1*x1 - 2*x2, 11)
]
sols = sy.solve(equations)
sols
{x1: 31/5, x2: -12/5}
Die zu lösenden Gleichungen wurden hier einfach in eine Liste gepackt und dem solve-Befehl übergeben. Das Ergebnis ist hier ein Objekt vom Typ
type(sols)
dict
Dictionary ist auch eine Containerklasse, welche Key-Value-Paare abspeichert. Der Key (Schlüssel) ist hier der Name der Variable und der Value deren Wert. Wir können auch mit einer for-Schleife über ein Dictionary iterieren. Die lokale Variable a in folgendem Beispiel ist dabei lediglich der Schlüssel. Den zugehörigen Wert bekommt man mit sols[a]:
print("Die Lösung unseres Gleichungssystems lautet")
for a in sols:
print(a, "=", sols[a])
Die Lösung unseres Gleichungssystems lautet
x1 = 31/5
x2 = -12/5
Alternativ lassen sich lineare Gleichungssysteme auch mit den Befehl sympy.linsolve(...) lösen:
x1, x2, x3 = sy.symbols('x1, x2, x3')
sols = sy.linsolve([2*x1+3*x2-6*x3 - 3, 1*x1-3*x2+3*x3 - 2], (x1,x2,x3))
sols
Für dieses System aus 2 Gleichungen und 3 Unbekannten hat der linsolve-Befehl eine Lösung ermittelt, die noch von \(x_3\) abhängt. Natürlich erwarten wir in diesem Beispiel unendlich viele Lösungen. Mit der subs-Methode können wir die freie Variable mit einem speziellen Wert substituieren:
for sol in sols:
print("Allgemeine Lösung :", sol)
print("Spezielle Lösung :", sol.subs('x3', 0))
print("Spezielle Lösung :", sol.subs('x3', 2))
Allgemeine Lösung : (x3 + 5/3, 4*x3/3 - 1/9, x3)
Spezielle Lösung : (5/3, -1/9, 0)
Spezielle Lösung : (11/3, 23/9, 2)
6.3. Gewöhnliche Differentialgleichungen¶
Auch einfache Differentialgleichungen können mit SymPy gelöst werden. Zunächst müssen wir dafür eine Differentialgleichung definieren. Dazu legen wir zunächst ein Objekt vom Typ Function an und definieren die Differentialgleichung als mathematischen Ausdruck. Die Funktion Derivative erlaubt es die Ableitungen der gesuchten Funktion einzuarbeiten:
y = sy.Function('y')
ode = sy.Derivative(y(x),x,x) + 2*sy.Derivative(y(x),x) - 6*y(x) - sy.exp(3*x)
ode
Die Funktion zum Lösen der Differentialgleichung ist sympy.dsolve (das “d” steht für differential equation). Wir übergeben den eben für die ODE definierten Ausdruck sowie die Funktion nach der wir diese lösen sollen:
sol = sy.dsolve(ode, y(x))
sol
type(sol)
sympy.core.relational.Equality
Das Ergebnis ist ein Objekt vom Tyo Equality, bestehend aus einer linken und einer rechten Seite einer Gleichung. Um die rechte Seite zu extrahieren und daraus eine Funktion zu definieren nutzen wir
f = sol.rhs
type(f)
sympy.core.add.Add
Unsere eben berechnete Funktion hängt von folgenden Variablen ab:
f.free_symbols
{C1, C2, x}
Dass unsere Lösung von 2 beliebigen Konstanten C1 und C2 abhängt ist nicht verwunderlich, da wir keine Anfangsbedingungen für unsere Differentialgleichung zweiter Art definiert haben. Wir können nun auch feste Werte für die Konstanten wählen. Dazu definieren wir ein Dictionary und nutzen die Funktion subs (Substituiere):
constants = {'C1': 1, 'C2': 3} # Dictionary anlegen
my_f = f.subs(constants) # Konstanten durch Werte ersetzen
my_f
Unsere Funktion my_f hängt nun nur noch von x ab und wir können wie gewohnt weiter arbeiten:
sy.plot(my_f, (x,0,2))
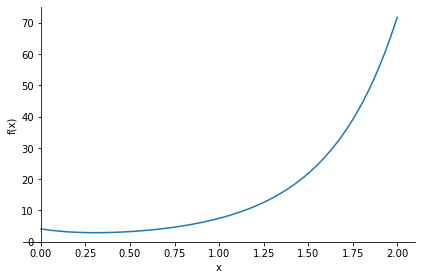
<sympy.plotting.plot.Plot at 0x7f4cd9caa620>
Schauen wir uns nun noch an, wie wir Anfangswertprobleme, also Differentialgleichungen zusammen mit entsprechenden Anfangsbedingungen, lösen können. Ruft man mit sp.dsolve? den Hilfetext zur Funktion dsolve auf, stößt man schnell auf den Parameter ics. Dieser soll ein Dictionary sein, welches alle Anfangs- und Randbedingungen beinhaltet. Dafür soll folgende Syntax genutzt werden:
initial_conditions = {y(0) : 0, # y(0) = 0
y(x).diff(x).subs(x, 0) : 1} # y'(0)= 1
Wir haben hier die Anfangsbedingungen \(y(0)=0\) und \(y'(0)=1\) vorgegeben. Der Aufruf von dsolve ergibt nun:
sol = sy.dsolve(ode, y(x), ics=initial_conditions)
f = sol.rhs
f
Offensichtlich hängt die Lösung nur noch von der Variablen \(x\) ab. Klar, da die Konstanten in der allgemeinen Lösung durch die Anfangsbedingungen eliminiert wurden.
f aus oberem Block ist wieder ein mathematischer Ausdruck, mit dem wir wie gewohnt weiter arbeiten können:
print("f ist vom Typ", type(f))
sy.plot(f, (x,0,1))
f ist vom Typ <class 'sympy.core.add.Add'>
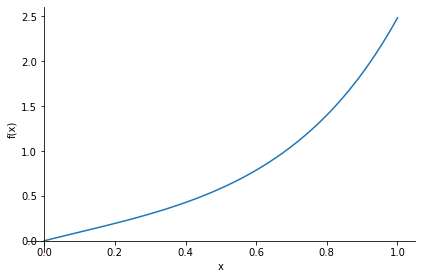
<sympy.plotting.plot.Plot at 0x7f4c8e197d90>
In folgendem Beispiel wird die Riccati-Differentialgleichung
gelöst. Interessant ist auch die Ausgabe der Funktion sympy.classify_ode(...). SymPy analysiert die Differentialgleichung und wendet, abhängig von der Klassifikation der Gleichng, eine entsprechende Lösungsstrategie an:
ode = sy.Derivative(y(x),x) + y(x)**2 + 2/x*y(x) + 2/(x**2)
sy.classify_ode(ode)
('1st_rational_riccati',
'Riccati_special_minus2',
'separable_reduced',
'lie_group',
'separable_reduced_Integral')
sol = sy.dsolve(ode, y(x))
sol
f = sol.rhs
my_f = f.subs('C1', 1)
my_f
