The ILOG CPLEX Barrier Optimizer is well suited to large, sparse problems. An alternative to the simplex optimizers, it exploits a primal-dual logarithmic barrier algorithm to generate a sequence of strictly positive primal and dual solutions to a problem. Like the simplex optimizers, it is not really necessary to understand the internal workings of barrier in order to obtain its performance benefits. However, for the interested reader, we first pause to give an outline of how it works.
ILOG CPLEX finds the primal solutions, conventionally denoted (x, s), from the primal formulation:
Minimize cTx
subject to Ax = b
with these bounds x + s = u and x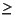 
l
where A is the constraint matrix, including slack and surplus variables; u is the upper and l the lower bounds on the variables.
Simultaneously, ILOG CPLEX automatically finds the dual solutions, conventionally denoted (y, z, w) from the corresponding dual formulation:
Maximize bTy - uTw + lTz
subject to ATy - w + z = c
with these bounds w 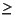0 and z 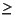0
All possible solutions maintain strictly positive primal solutions (x - l, s) and strictly positive reduced costs (z, w) so that the value 0 (zero) forms a barrier for primal and dual variables within the algorithm.
ILOG CPLEX measures progress by considering the primal feasibility, dual feasibility, and duality gap at each iteration. To measure feasibility, ILOG CPLEX considers the accuracy with which the primal constraints (Ax = b, x + s = u) and dual constraints (ATy + z - w = c) are satisfied. The optimizer stops when it finds feasible primal and dual solutions that are complementary. A complementary solution is one where the sums of the products (xj -lj)zj and (uj - xj)zj are within some tolerance of 0 (zero). Since each (xj -lj), (uj - xj), and zj is strictly positive, the sum can be near zero only if each of the individual products is near zero. The sum of these products is known as the complementarity of the problem.
On each iteration of the barrier optimizer, ILOG CPLEX computes a matrix based on AAT and then computes a Cholesky factor of it. This factored matrix has the same number of nonzeros on each iteration. The number of nonzeros in this matrix is influenced by the barrier ordering parameter.
The ILOG CPLEX Barrier Optimizer is appropriate and often advantageous for large problems, for example, those with more than 1000 rows or columns. It is effective on problems with staircase structures or banded structures in the constraint matrix. It is also effective on problems with a small number of nonzeros per column.
Its performance is most dependent on these characteristics:
To decide whether to use the barrier optimizer on a given problem, you should look at both these characteristics. (We explain how to check those characteristics later in this chapter in "Cholesky Factor in the Log File" , and "Nonzeros in Lower Triangle of AAT in the Log File" ).
Since many users prefer basic solutions because they can be used to restart simplex optimization, the ILOG CPLEX Barrier Optimizer includes basis crossover algorithms. By default, the barrier optimizer automatically invokes a primal crossover when the barrier algorithm terminates (unless termination occurs abnormally because of insufficient memory or numerical difficulties). Optionally, you can also execute barrier optimization with a dual crossover or with no crossover at all. The section "Controlling Crossover" explains how to control crossover in the Interactive Optimizer.
The barrier optimizer and the simplex optimizers (primal and dual) are fundamentally different approaches to solving linear programming problems. The key differences between them have these implications:
- The fact that barrier without crossover does not produce a basic solution has other consequences. Without a basis, you will not be able to optimize the same or similar problems repeatedly using advanced start information. You will also not be able to obtain range information for performing sensitivity analysis.
