6.9 Der DK-Automat

Von der Grammatik $\hat{G}$ zu einem nichtdeterministischen endlichen Automaten

Um den $L R (0)$ -Parser gemäß Algorithmus 5.8.7 zu implementieren, müssen wir den Test $γ \overset{?}{\in} Front (G)$ durchführen und, falls die Antwort ja ist, die Blüte finden. Dies gelingt uns, indem wir die Grammatik $\hat{G}$ in einen endlichen Automaten umwandeln. Theorem 4.3.8 und die ihm vorhergehende Konstruktion zeigen, wie man das macht. Anstatt allerdings das Theorem als "black box" zu verwenden, gehen wir die Konstruktion anhand zweier fiktiver Produktion $X \to a B c D e$ und $X \to u V w$ Schritt für Schritt durch. Wir erkennen die Terminale $Σ = {a, c, e, u, w}$ und die Nichtterminale $N = {X, B, D, V}$ . In $\hat{G}$ sind \{a,c,e,u,w,A,B,D,V\} alles Terminale, und die Nichtterminale sind $\hat{N} = {\hat{X}, \hat{B}, \hat{D}, \hat{V}} .$ Die Produktionen von $\hat{G}$ sind $\begin{aligned} \hat{X} & \to a \hat{B} \\ \hat{X} & \to a B c \hat{D} \\ \hat{X} & \to a B c D e \\ \hat{X} & \to u \hat{V} \\ \hat{X} & \to u V w \end{aligned}$

Diese übersetzen wir in einen verallgemeinert nichtdeterministischen Automaten, bei dem jede Kante mit einem Wort $β \in (Σ \cup N)^{*}$ , also aus Terminalen der Grammatik $\hat{G}$ beschriftet ist:

Wir brechen die Kanten in Stücke, so dass jede mit genau einem Zeichen beschriftet ist:

Nochmal: jede Kante ist mit einem Terminalsymbol beschriftet. Die Symbole $B, D, V$ sind Terminale in der Grammatik $\hat{G}$ . Wenn wir $ϵ$ -Übergänge zulassen, können wir den Automaten übersichtlicher gestalten und mehrere Zustände zusammenfassen:

Wir werden uns noch bessere Namen für die Zwischenzustände ausdenken. Wenn wir uns an die Rechtsableitungsbäume mit Stamm, linkem Rand, Blüte und rechtem Rest erinnern, dann haben die Zwischenzustände eine klare Bedeutung: der Zustand $4$ oben zum Beispiel bedeutet, dass der Knoten $X$ im Stamm mit $a, B, c, D, e$ beschriftete Kinder hat und wir uns bereits entschieden haben, dass $a$ , $B$ und $c$ Blätter sein sollen, also zum linken Rand gehören. Der Übergang $4 \overset{D}{\to} 5$ entspricht dann der Entscheidung, auch $D$ zu einem Blatt zu machen, während $4 \overset{ϵ}{\to} \hat{D}$ der Entscheidung entspricht, $D$ zu einem Knoten im Stamm zu machen und eine $D$ -Produktion anzuwenden. Die beiden $ϵ$ -Übergänge von $\hat{X}$ nach $1$ bzw. $7$ stellen einfach sicher, dass wir uns erst entscheiden, mit welcher Produktion wir den Stammknoten $X$ expandieren, bevor wir weitermachen. Daher nennen wir Zustand $4$ um in $X \to a B c . D e$ , wobei der Punkt $.$ markiert, welchen Teil der rechten Seite wir bereits gelesen haben. Wir erhalten folgendes Bild:

Die $a^{m + k} b^{m}$ -Grammatik

Wir illustrieren obige Vorgehensweise nun anhand der Grammatik

$\begin{aligned} G & : \\ S & \to a S \\ S & \to B \\ B & \to a B b \\ B & \to a b \end{aligned}$

Laut Gebrauchsanweisung aus dem letzten Teilkapitel hat die Grammatik $\hat{G}$ die Terminalsymbole $Σ \cup N = {a, b, S, B}$ und die Nichtterminale $\hat{N} = {\hat{S}, \hat{B}}$ . Die Produktionen von $\hat{G}$ ergeben sich wie folgt:

\begin{array}{r} \begin{array}{ll} Produktion in G & Produktion in \hat{G} \\ S \to a S & \hat{S} \to a \hat{S} \\ \hat{S} \to a S \\ S \to B & \hat{S} \to \hat{B} \\ \hat{S} \to B \\ B \to a B b & \hat{B} \to a \hat{B} \\ \hat{B} \to a B b \\ B \to a b & \hat{B} \to a b \end{array} \end{array}

In dieser Grammatik betrachten wir die Rechtsableitung

\begin{array}{r} S \overset{}{⟹} a S \overset{}{⟹} a a S \overset{}{⟹} a a B \overset{}{⟹} a a a B b \overset{}{⟹} a a a a B b b \overset{}{⟹} a a a a a B b b b \end{array}

Es gilt $front (a a a a a B b b b) = a a a a a B b$ . In $\hat{G}$ entspricht die obige Rechtsableitung der Ableitung

\begin{array}{r} \hat{S} \overset{}{⟹} a \hat{S} \overset{}{⟹} a a \hat{S} \overset{}{⟹} a a \hat{B} \overset{}{⟹} a a a \hat{B} \overset{}{⟹} a a a a B b \end{array}

Den nichtdeterministischen DK-Automaten (mit $ϵ$ -Übergängen) können wir nun Schritt für Schritt zeichnen:

Der nichtdeterministische DK-Automat

Definition 6.9.1 Für eine kontextfreie Grammatik ist der nichtdeterministische DK-Automat (NDK-Automat) ein nichtdeterministischer endlicher Automat mit $ϵ$ -Übergängen, den wir wie folgt konstruieren:

Für jede Produktion $X \to β$ gibt es einen Zustandsübergang $X \overset{ϵ}{\to} X \overset{}{\to} . β$
Für jede Zerlegung $β = β_{1} σ β_{2}$ gibt es den Zustandsübergang $X \overset{}{\to} β_{1} . σ β_{2} \overset{σ}{\to} X \overset{}{\to} β_{1} σ . β_{2}$
Falls $σ$ ein Nichtterminal $Y$ ist, also $β = β_{1} Y β_{2}$ , gibt es zusätzlich noch den Übergang $X \overset{}{\to} β_{1} . Y β_{2} \overset{ϵ}{\to} Y$

Die Interpretation dieser Übergänge in Rechtsableitungsbaum-Begriffen ist: (1) heißt, dass $X$ ein Stammknoten ist und wir ihn anhand der Regel $X \to β$ expandieren; wir erschaffen also Kinder, die mit den Symbolen von $β$ beschriftet sind. (2) heißt, dass wir uns bereits entschieden haben, die Kinder $β_{1}$ von $X$ nicht zu expandieren, sie also zum linken Rand werden zu lassen, und diese Entscheidung nun auch für das Symbol $σ$ treffen; (3) bedeutet, dass wir uns entschließen $σ$ (das hier ein Nichtterminal $Y$ ist) weiter zu expandieren, es also nicht dem linken Rand zuordnen, sondern zu einem Stammknoten werden lassen, uns aber noch nicht entschlossen haben, welche Produktion $Y \to ?$ wir anwenden wollen.

Der Startzustand ist $S$ . Jeder Zustand der Form $X \overset{}{\to} β .$ ist ein akzeptierender Zustand.

Den NDK-Automaten deterministisch machen

Wir wissen ja bereits, wie man einen nichtdeterministischen Automaten deterministisch macht: die Potenzmengenkonstruktion aus Kapitel 4.3. Hier können wir diese leider nicht direkt anwenden, da der obige Automat $ϵ$ -Übergänge hat. Wie geht das also nun? Im deterministischen Automaten ist wie bei der Potenzmengenkonstruktion jeder Zustand eine Menge $R$ von Zuständen des nichtdeterministischen Automaten. Wenn wir nun in eine solche Menge $R$ einen Zustand $q$ einfügen, dann fügen wir auch alle Zustände $q^{'}$ hinzu, zu denen es einen $ϵ$ -Übergang $q \overset{ϵ}{\to} q^{'}$ gibt. Für den obigen nichtdeterministischen Automaten sieht das dann so aus:

Der NDK-Automat

Der Anfangszustand ${S}$

Wir fügen alle Zustände hinzu, die wir per $ϵ$ -Kanten erreichen können.

Dann gehen wir wie gewohnt vor. Nur einer der fünf Zustände in unserem Korb hat einen $\overset{B}{\to}$ -Übergang. Dies ist ein akzeptierender Zustand.

Alle diese haben einen $\overset{a}{\to}$ -Übergang.

Die $\overset{a}{\to}$ -Übergänge führen hierhin.

Die $\overset{a}{\to}$ -Übergänge führen hierhin. Und per $ϵ$ -Übergängen auch hierhin.

Jetzt ist der Zustand fertig.

Wieder haben drei Zustände einen $\overset{a}{\to}$ -Übergang.

Per $ϵ$ -Abschluss erhalten wir diese Menge.

Per $ϵ$ -Abschluss erhalten wir diese Menge. Sie ist mit der daneben identisch. Wir ersetzen es also durch eine Selbstschleife.

Noch ein Ausgang $\overset{S}{\to}$ . Der Automat ist fertig.

Und hier nochmal das Endergebnis, wobei wir die Zustände im DK-Automaten durchnummeriert haben:

Streng genommen ist das Ergebnis kein deterministischer Automat, da zum Beispiel der Startzustand keinen $b$ -Übergang hat. Die Zustandsübergangsfunktion $δ : Q \times Σ \to Q$ ist gar keine Funktion, sondern eine partielle Funktion, da $δ (q, σ)$ für manche Eingabewerte undefiniert ist. Wir verwenden aber die Konvention, dass der Automat in diesem Falle in einen Todeszustand wechselt, aus dem er nicht wieder herauskommt und der nicht akzeptierend ist. Dies ist übersichtlicher, als überall Todeskanten hinzuzufügen.

Den DK-Automaten verwenden

Wie verwenden wir jetzt den DK-Automaten? In jedem Parser-Schritt füttern wir den DK-Automaten mit dem Stack-Inhalt. Landet der Automat auf einem nichtaktzeptierenden Zustand, müssen wir ein weiteres Zeichen lesen, d.h. auf den Stack legen. Landet er auf einem akzeptierenden Zustand, so enthält dieser ein $X \to β .$ und wir reduzieren per $β \overset{}{↣} X$ . Nehmen wir $a a a b b$ als Beispiel:

\begin{array}{r} D K : 1 \overset{a}{\to} 3 \overset{a}{\to} 3 \overset{a}{\to} 3 \overset{b}{\to} 4 \end{array}

erst nach vier Zeichen landet der Automat in dem akzeptierenden Zustand $4$ . Wir reduzieren per $a b \overset{}{↣} B$ ; nun liegt $a a B$ auf dem Stack. Wir füttern das dem DK-Automaten:

\begin{array}{r} D K : 1 \overset{a}{\to} 3 \overset{a}{\to} 3 \overset{B}{\to} 5 \end{array}

Wir landen in dem akzeptierenden Zustand $5$ und reduzieren per $B \overset{}{↣} S$ . Der Stack ist nun $a a S$ . Das bringt uns nach

\begin{array}{r} 1 \overset{a}{\to} 3 \overset{a}{\to} 3 \overset{S}{\to} 7 \end{array}

und wir reduzieren per $a S \overset{S}{↣}$ ; der Stack ist nun $a S$ ; jetzt wiederholt sich der letzte Schritt, wir reduzieren noch einmal per $a S \overset{}{↣} S$ , und nun liegt $S$ auf dem Stack. Das Eingabewort ist noch nicht vollständig gelesen: das zweite $b$ fehlt noch. Wenn wir allerdings $S$ dem DK-Automaten füttern, landet der im Todeszustand und weiß nicht mehr weiter. Der Parse-Vorgang ist fehlgeschlagen. Was ist passiert?

Der Knackpunkt liegt bei Zustand $5$ . Dieser suggiert eine Reduktion $B \overset{}{↣} S$ . Allerdings wäre es auch möglich, ein weiteres Zeichen zu lesen (falls dies $b$ ist) und in Zustand $6$ zu landen. Sehen Sie: unser Parser hat im zweiten Schritt

\begin{array}{r} a a B b \overset{}{↣} a a S b \end{array}

reduziert, was kein korrekter Linksreduktionsschritt ist, weil $a a S b$ keine gültige Wortform ist. Wenn das $b$ aber nicht da wäre, wäre

\begin{array}{r} a a B \overset{}{↣} a S \end{array}

korrekt. Wir sehen also: $a a B w \overset{}{↣} a S w$ ist ein korrekter Schritt für $w = ϵ$ , aber nicht für $w = b$ , obwohl $a a B b$ selbst eine gültige Wortform ist. Die Grammatik verletzt also die LR(0)-Bedingung aus Definition 5.7.4. Die Korrektheit eines Linksreduktionsschritts $α β w \overset{}{↣} α X w$ kann also ohne Kenntnis von $w$ gar nicht sichergestellt werden.

Die Grammatik abändern: Stopper-Zeichen am Schluss

In diesem Fall lässt sich das Dilemma flicken, indem wir ein Stopperzeichen am Ende einfügen. Wir ändern die Grammatik leicht ab:

\begin{aligned} G_{z} & : \\ S & \to a S \\ S & \to B z \\ B & \to a B b \\ B & \to a b \end{aligned}

Es gilt also $L (G_{z}) = L (G) \circ {z}$ , wir hängen also jedem $G$ -Wort ein $z$ an. Wie sieht der NDK- und der DK-Automat aus?

Das $z$ verhindert, dass der Parser verfrüht $B \overset{}{↣} S$ reduziert und zwingt ihn, damit zu warten, bis das Ende des Inputs erreicht ist. Wenn wir den Automaten betrachten, sehen wir, dass kein akzeptierender Zustand eine ausgehende Kante hat: wenn also $γ \in Front (G_{z})$ ist, dann gibt es kein $γ γ_{1} \in Front (G_{z})$ mit $| γ_{1} | > 0$ . In anderen Worten: die Sprache $Front (G_{z})$ ist präfixfrei. Es kann also keinen Zweifel geben, dass bei Erreichen eines akzeptierenden Zustandes reduziert werden muss.

Die Klammern-Grammatik

Als nächstes Beispiel schauen wir uns eine Grammatik an, die die wohlgeformten Klammerausdrücke generiert:

\begin{aligned} G_{()} & : \\ S & \to ϵ \\ S & \to S (S) \end{aligned}

mit den Terminalen ${(,)}$ und dem einen Nichtterminal $S$ . Diese Grammatik hat mit $S \to ϵ$ die gewöhnungsbedürftige Eigenschaft, dass der Reduktionsschritt $w \overset{}{↣} S w$ immer technisch möglich wäre (wenn auch nicht immer korrekt). NDK- und DK-Automat sind schnell gezeichnet:

Auch in diesem Automaten haben akzeptierende Zustände ausgehende Kanten, die zu weiteren akzeptierenden Zuständen führen. Somit ist $Front (G_{()})$ auch nicht präfixfrei. In der Tat sind

\begin{array}{r} ϵ, S (, S (S (, S (S (S) \end{array}

alles Wörter in $Front (G_{()})$ . Das ist in diesem Kontext aber nicht schlimm: wenn wir entscheiden wollen, ob

\begin{array}{r} α β w \overset{}{↣} α X w \end{array}

ein gültiger Linksreduktionsschritt ist, dann kennen wir $w$ zwar noch nicht, wissen aber, dass $w \in Σ^{*}$ gilt, da $w$ ja der ungelesene Teil des Eingabewortes ist; insbesondere kann das erste Zeichen von $w$ kein Nichtterminal sein. Insofern können wir dem DK-Automaten für $G_{()}$ trauen: wenn er uns in einen akzeptierenden Zustand führt, können wir reduzieren.

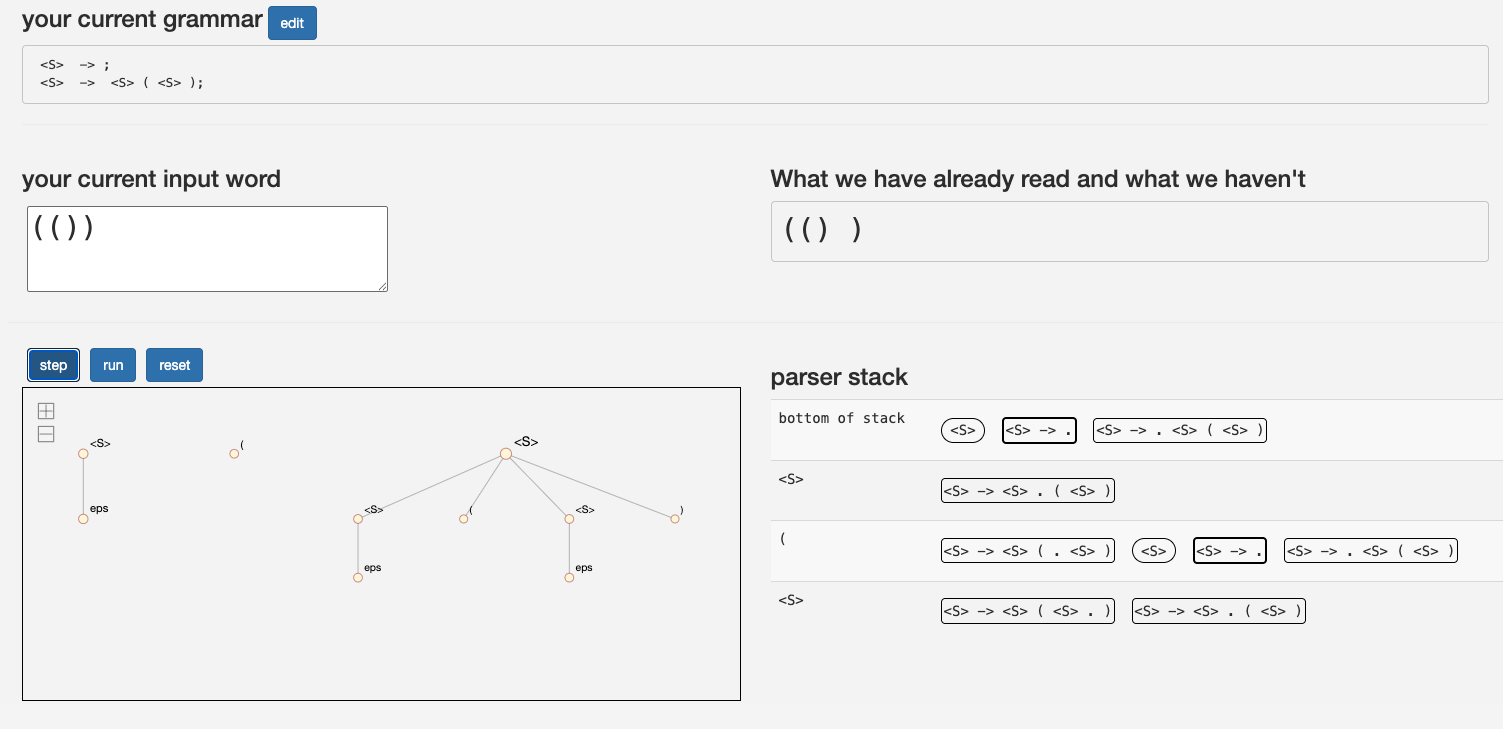
Übungsaufgabe 6.9.1 Lassen Sie den LR-Parser auf $(() ()) ()$ laufen und protokollieren Sie Stackinhalt und Zustand des DK-Automaten.

Übungsaufgabe 6.9.2 Zeichnen Sie NDK-Automaten und DK-Automaten für die Grammatik

\begin{aligned} S & \to ϵ \\ S & \to S (S) \end{aligned}

und zeigen Sie, dass diese nicht LR(0) ist. Finden Sie also eine Produktion $X \to β$ und gültige Wortformen $α β w$ und $α β w^{'}$ , so dass $α X w$ gültig ist, nicht aber $α X w^{'}$ .

Übungsaufgabe 6.9.3 Untersuchen Sie unsere Arithmetik-Grammatik:

\begin{aligned} E & \to (E + E) \\ E & \to (E * E) \\ E & \to N \\ N & \to D \\ N & \to N D \\ D & \to 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 \end{aligned}

Zeichnen Sie NDK- und DK-Automaten und zeigen Sie, dass die Grammatik nicht LR(0) ist.

Challenge. Fügen wir den arithmetischen Ausdrücken noch ein Schlusszeichen $;$ hinzu, also $(2 + (4 * 3));$ statt $(2 + (4 * 3))$ . Wenn wir obige Grammatik um die Regel $S \to E;$ ergänzen und $S$ zum Startsymbol machen, ist sie dann LR(0)? Wenn nicht: können Sie die Grammatik umschreiben (also eine äquivalente, d.h. die gleiche Sprache produzierende Grammatik angeben), so dass sie LR(0) wird?

Der DK-Test

Wir beschreiben nun, wie man algorithmisch testet, ob eine gegebene Grammatik die LR(0)-Bedingungen erfüllt.

Theroem 6.9.2 (DK-Test). Sei $G$ eine kontextfreie Grammatik ohne nutzlose Nichtterminale und ei $M$ der DK-Automat für die Grammatik $G$ . Die Grammatik $G$ ist LR(0) genau dann, wenn folgende zwei Bedingungen gelten:

(DK.1) Ein akzeptierender Zustand von $M$ (der ja eine Menge von Zuständen des NDK-Automaten ist) enthält genau einen akzeptierenden NDK-Zustand, also genau ein $X \to β .$
(DK.2) Wenn $q$ ein akzeptierender Zustand von $M$ ist und $q \overset{σ}{\to} q^{'}$ , dann ist $σ$ ein Nichtterminal.

Wenn diese beiden Bedingungen gelten, sagen wir, dass $G$ den DK-Test bestanden hat. Das Theorem sagt also: $G$ ist LR(0) genau dann, wenn es den DK-Test besteht.

Beweisskizze. Wir erinnern den Leser noch einmal an die alternative Charakterisierung von LR(0)-Sprachen, nämlich :

Lemma 5.7.5, noch einmal (LR(0), äquivalente Formulierung). Eine Grammatik $G$ ist LR(0) genau dann, wenn für alle korrekten Linksreduktionsschritte $α β w \overset{}{↣} α X w$ und $α^{'} β^{'} w^{'} \overset{}{↣} α^{'} X^{'} w^{'}$ gilt:

Falls $α β = α^{'} β^{'}$ dann auch $β = β^{'}$ und $X = X^{'}$ ; in Worten: wenn die Fronten identisch sind, dann auch die Reduktionsschritte.
Wenn $α^{'} β^{'} = α β φ$ und $| φ | \geq 1$ , dann $φ \notin Σ^{*}$ ; in Worten: wenn $front (γ)$ ein echter Präfix von $front (γ^{'})$ ist, dann muss in dem überstehenden Teil von $front (γ)$ mindestens ein Nichtterminal vorkommen.

Es ist nicht schwer zu sehen, dass (DK.1) äquivalent zu Punkt 1 des Lemmas ist. Wenden wir uns (DK.2) und Punkt 2 zu. Wenn Punkt 2 nicht gilt, dann gibt es korrekte Reduktionsschritte

\begin{array}{r} α β w \overset{}{↣} α X w \\ α β σ w^{'} = α^{'} β^{'} w^{'} \overset{}{↣} α^{'} X^{'} w^{'} \end{array}

Wenn wir dem Automaten den Präfix $α β$ füttern, bringt er uns in einen Zustand, der die $X \to β .$ enthält, da $α β$ ja eine Front ist. Dieser Zustand muss allerdings einen Übergang haben, der mit $σ$ gelabelt ist, dem ersten Zeichen von $φ$ , da ja $α β σ$ ein Präfix der Front $α^{'} β^{'}$ ist. Somit gilt (DK.2) nicht.

Wenn umgekehrt (DK.2) nicht gilt, dann gibt es einen akzeptierenden Zustand $q$ (der also $X \to β .$ enthält) und eine ausgehende Kante $q \overset{σ}{\to} q^{'}$ mit einem Terminal $σ$ .

Übungsaufgabe 6.9.4 Zeigen Sie: wenn $G$ keine nutzlosen Nichtterminale hat, dann gibt es im NDK-Automaten für jeden Zustand $q$ eine Übergangsfolge $q \overset{v}{\to^{*}} q^{'}$ zu einem akzeptierenden Zustand $q^{'}$ , wobei $v$ ausschließlich aus $G$ -Terminalen besteht, also $v \in Σ^{*}$ .

Zeigen Sie das selbe für den DK-Automaten.

Es gibt also einen Weg $q \overset{σ}{\to} q^{'} \overset{v}{\to^{*}} q^{″}$ für $v \in Σ^{*}$ und einen akzeptierenden Zustand $q^{″}$ . Es sind also sowohl $α β$ als auch $α β σ v$ Fronten von $G$ , und $σ v$ besteht nur aus Terminalen. Das heißt, dass Punkt 2 der Schlussfolgerung nicht gilt. $◻$

LR(1)-Grammatiken

Hier ist der nichtdeterministische Automat für

G

mit Lookahead 1.

Jetzt machen wir den Automaten deterministisch: