In diesem Kapitel will ich Sie davon überzeugen, dass SAT so etwas wie eine universelle Modellierungssprache darstellt, für eine bestimmte Art von Problemen. Wir werden konkret Probleme als CNF codieren und dann mithilfe von SAT-Solvern lösen. Sicherlich kennen Sie Sudokus:

Diese sind beliebte Rätsel, in denen in einem $9\times 9$-Gitter einige Zahlen vorgegeben sind. Man muss die leeren Zellen so ausfüllen, dass

  1. In jeder Zelle eine Zahl steht,
  2. keine Zahl in einer Zeile doppelt vorkommt,
  3. keine Zahl in einer Spalte doppelt vorkommt,
  4. keine Zahl in einem der neun $3 \times 3$-Unterblöcke doppelt vorkommt.

Im Folgenden will ich ein Programm schreiben, mit dem ich Sudokus auf dem Computer lösen kann. Ich will aber nicht das Rad neu erfinden. Daher werden wir das Sudoku als SAT-Problem codieren und dann mit SAT-Solvern lösen. Als erstes müssen wir uns überlegen, was für Variable unsere Formel haben soll und was diese Variablen bedeuten. Hier ist eine Möglichkeit: fur $1 \leq i, j, c \leq 9$ codiert die Variable

\begin{align*} x_{ijc} \ , \end{align*}

ob Zelle $(i,j)$ im Sudoku den Wert $c$ bekommen soll. Wenn also $x_{462}$ True ist, dann soll in der sechsten Zelle der vierten Zeile (also rechts von $3$ und $4$) die Zahl $2$ stehen. Insgesamt haben wir $9 \cdot 9 \cdot 9 = 729$ Variable. Nun müssen wir die Regeln des Sudokus codieren.

  1. In jeder Zelle steht eine Zahl. Für Zelle $(i,j)$ können wir das mit der Klausel \begin{align*} (x_{ij1} \vee x_{ij2} \vee \dots \vee x_{ij9}) \end{align*} ausdrücken. Dies ergibt $81$ Klauseln.
  2. In keine Zeile gibt es eine Zahl, die doppelt vorkommt. Das ist schon schwieriger. Wie wäre es mit: Für jede Zeile $i$ und jedes Paar $\{j_1, j_2\}$ von zwei Spalten soll $G^i_{j_1,j_2}$ gelten, wobei dann $G^i_{j_1,j_2}$ die Aussage in $(i,j_1)$ und $(i,j_2)$ müssen verschiedene Werte stehen ist. Also: \begin{align*} \bigwedge_{i=1}^9 \bigwedge_{ \{j_1, j_2\} \in {[9]\choose 2}} G^i_{j_1,j_2} \ , \end{align*} Jetzt müssen wir noch $G^i_{j_1, j_2}$ als CNF-Formel schreiben. Wie geht das? Nun ja, für jeden Wert $1 \leq c \leq 9$ muss gelten, dass Zellen $(i, j_1)$ und $(i, j_2)$ nicht beide Wert $c$ haben dürfen. Also: \begin{align*} G^i_{j_1,j_2} := \bigwedge_{c=1}^9 \left(\bar{x}_{ij_1c} \vee \bar{x}_{ij_2c}\right) \end{align*} und insgesamt also \begin{align*} \bigwedge_{i=1}^9 \bigwedge_{ \{j_1, j_2\} \in {[9]\choose 2}} \bigwedge_{c=1}^9 \left(\bar{x}_{ij_1c} \vee \bar{x}_{ij_2c}\right) \end{align*} Das sind $9 \cdot {9 \choose 2} \cdot 9 = 2.916$ Klauseln.
  3. In keine Zeile kommt eine Zahl doppelt vor. Das geht genau so wie in Punkt 2, nur mit vertauschten Indizes: \begin{align*} \bigwedge_{j=1}^9 \bigwedge_{ \{i_1, i_2\} \in {[9]\choose 2}} \bigwedge_{c=1}^9 \left(\bar{x}_{i_1jc} \vee \bar{x}_{i_2jc}\right) \end{align*} und somit nochmal $2.916$ Klauseln.
  4. In keinem Unterblock darf eine Zahl doppelt vorkommen. Das wird etwas umständlicher. Wir partitionieren die 81 Zellen, also $[9] \times [9]$, in neun Blöcke: \begin{align*} [9] \times [9] = \biguplus_{1 \leq i,j \leq 3} B_{ij} \end{align*} mit \begin{align*} B_{ij} = \{ (3(i-1) + x, 3(j-1) + y) \ | \ 1 \leq x,y \leq 3 \} \ . \end{align*} Die Formel ist dann \begin{align*} \bigwedge_{(a,b) \in [3]\times[3]} \bigwedge_{ \{(i_1,j_1), (i_2,j_2)\} \in {B_{ab} \choose 2}} \bigwedge_{c=1}^9 \left(\bar{x}_{i_1j_1c} \vee \bar{x}_{i_2j_2c}\right) \ , \end{align*} was nochmals $2.961$ Klauseln ergibt.

Dieser Teil ist für jedes $9 \times 9$-Sudoku identisch. Für das konkrete Sudoku müssen wir noch die vorgegebenen Werte codieren. Das ist einfach: wenn in dem Rätsel Zelle $(i,j)$ bereits mit Zahl $c$ ausgefüllt ist, dann fügen wir einfach die $1$-Klausel $(x_{ijc})$ unserer Formel hinzu. Für das obige Sudoku wäre dies

\begin{align*} & (x_{129}) \wedge (x_{138}) \wedge (x_{164}) \wedge (x_{172}) \wedge (x_{185}) \wedge \\ & (x_{242}) \wedge (x_{293}) \wedge \\ & (x_{335}) \wedge (x_{398}) \wedge \\ & (x_{433}) \wedge (x_{444}) \wedge (x_{471}) \wedge (x_{487}) \wedge \\ & (x_{516}) \wedge (x_{569}) \wedge \\ & (x_{692}) \wedge \\ & (x_{723}) \wedge (x_{757}) \wedge \\ & (x_{888}) \wedge \\ & (x_{937}) \wedge (x_{941}) \wedge (x_{975}) \wedge (x_{984}) \end{align*}

Der Workflow ist nun, dass wir (1) das Sudoku in eine CNF übersetzen; (2) diese von einem SAT-Solver lösen lassen; (3) dessen Output wieder in eine Sudoko-Lösung zurückübersetzen.

Implementierung und Ausführung.

Das Sudoku von oben habe ich in der Datei 01-sudoku.txt codiert.

  1. Das Programm sudoku-to-sat.py übersetzt das Sudoku in eine CNF im DIMACS-CNF-Format. Das Ergebnis sehen Sie in der Datei 01-cnf.txt.
  2. Wir rufen den SAT-Solver MiniSAT auf. Das Ergebnis (also hier die erfüllende Belegung) speichern wir in 01-assignment.txt. Dies enthält alle $729$ Literale, ist also recht unübersichtlich.
  3. Mit sat-assignment-to-sudoku-solution.py decodieren wir die erfüllende Belegung in eine Sudoku-Lösung. Diese finden Sie in der Datei 01-solution.txt. 
python sudoku-to-sat.py < 01-sudoku.txt  > 01-cnf.txt                            
minisat 01-cnf.txt 01-assignment.txt
[output not shown]
python sat-assignment-to-sudoku-solution.py < 01-assignment.txt
7 9 8 | 3 1 4 | 2 5 6 
1 4 6 | 2 8 5 | 7 9 3 
3 2 5 | 6 9 7 | 4 1 8 
------+-------+------
9 8 3 | 4 6 2 | 1 7 5 
6 1 2 | 7 5 9 | 8 3 4 
5 7 4 | 8 3 1 | 9 6 2 
------+-------+------
4 3 9 | 5 7 8 | 6 2 1 
2 5 1 | 9 4 6 | 3 8 7 
8 6 7 | 1 2 3 | 5 4 9

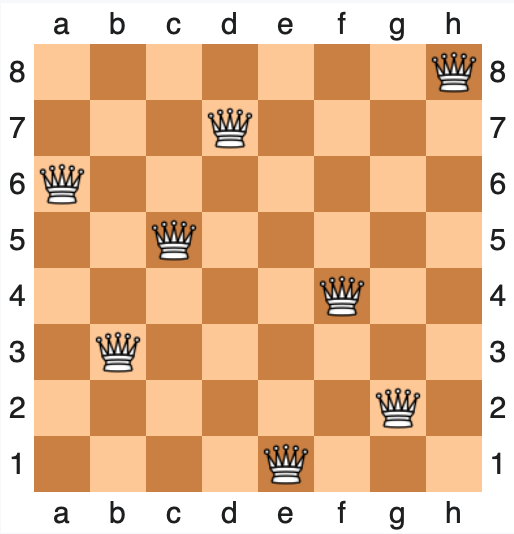
Übungsaufgabe Das Damenproblem fragt, ob man acht Damen so auf ein Schachbrett positionieren kann, dass keine zwei sich bedrohen (also: pro Spalte, Zeile und Diagonale jeweils höchstens eine Dame). Hier ist eine Lösung:


Quelle: Screenshot von Wikipedia
Das Damenproblem kann man natürlich für jede natürliche Zahl $n$ stellen. Hierbei will man $n$ Damen auf ein $n \times n$-Schachbrett stellen. Modellieren Sie das Damenproblem als CNF-Formel.

Weitere Probleme als SAT modellieren

Problem (3-Colorability). Gegeben ein Graph $G = (V,E)$. Gibt es eine Färbung $c: V \rightarrow \{\texttt{rot},\texttt{gruen},\texttt{blau}\}$ der Knoten mit drei Farben, so dass keine zwei benachbarten Knoten die selbe Farbe haben, also mit

\begin{align*} \forall \ \{u,v\} \in E: c(u) \ne c(v) \quad ? \end{align*}

3-Colorability als CNF modellieren. Seien $v_1, \dots, v_n$ die Knoten des Graphen. Wir führen $3n$ Boolesche Variable ein: $r_1, \dots, r_n, g_1, \dots, g_n, b_1, \dots, b_n$. Die Intention hierbei ist, dass $r_i$ anzeigt, ob $v_i$ rot ist und so weiter. Wir müssen jetzt Klauseln erschaffen, die die Aussage "das ist eine gültige 3-Färbung" als CNF-Formel codieren. Wir erschaffen folgende Klauseln:

\begin{align*} & (r_i \vee g_i \vee b_i) \tag{$v_i$ hat mindestens eine Farbe}\\ & (\bar{r}_i \vee \bar{g}_i) \wedge (\bar{r}_i \vee \bar{b}_i) \wedge (\bar{g}_i \vee \bar{b}_i) \tag{$v_i$ hat nicht zwei Farben gleichzeitig} \end{align*}

Dies tun wir für jedes $i$. Wir sehen nun: jede Belegung, die die obigen Klauseln erfüllt, entspricht einer $3$-Färbung $c: V \rightarrow \{1,2,3\}$, und umgekehrt. Nun müssen wir die Aussage Kante $\{v_i,v_j\}$ ist gültig gefärbt formulieren:

\begin{align*} & (\bar{r}_i \vee \bar{r}_j) \tag{$v_i$ und $v_j$ sind nicht beide rot}\\ & (\bar{g}_i \vee \bar{g}_j) \tag{$v_i$ und $v_j$ sind nicht beide grün}\\ & (\bar{b}_i \vee \bar{b}_j) \tag{$v_i$ und $v_j$ sind nicht beide blau}\\ \end{align*}

und dann alles zusammenwerfen:

\begin{align*} F:= & \quad \bigwedge_{i=1}^n \left( (r_i \vee g_i \vee b_i) \wedge(\bar{r}_i \vee \bar{g}_i) \wedge (\bar{r}_i \vee \bar{b}_i) \wedge (\bar{g}_i \vee \bar{b}_i) \right) \wedge \\ & \bigwedge_{\{v_i, v_j\} \in E} \left( (\bar{r}_i \vee \bar{r}_j) \wedge (\bar{g}_i \vee \bar{g}_j) \wedge (\bar{b}_i \vee \bar{b}_j) \right) \end{align*}

Übungsaufgabe Sei $G = (V,E)$ ein Graph. Ein Matching ist eine Menge $M \subseteq E$ an Kanten, die sich nicht berühren. Formal: \begin{align*} \forall e_1, e_2 \in M: \ e_1 = e_2 \textnormal{ oder } e_1 \cap e_2 = \emptyset \ . \end{align*} Ein perfektes Matching ist ein Matching, das jeden Knoten berührt, also $|M| = |V|/2$. Perfect Matching ist das entsprechende Entscheidungsproblem: Gegeben ein Graph, hat er ein perfektes Matching? Wenn Sie ein Suchproblem wollen, dann gerne auch finde so ein perfektes Matching.

Modellieren Sie Perfect Matching als CNF.

Übungsaufgabe Eine unabhängige Menge in einem Graphen $G = (V,E)$ ist eine Menge $I \subseteq V$ von Knoten, zwischen denen keine Kante verläuft, also

\begin{align*} \forall \{u,v\} \in E: \ \{u,v\} \not \subseteq I \end{align*}

Beim Entscheidungsproblem Independent Set ist ein Graph $G$ und eine Zahl $k \in \N$ gegeben und die Frage ist, ob es in $G$ eine unabhängige Menge der Größe $k$ gibt.

Modellieren Sie Independent Set als CNF. Hierbei ist die Aussage $I$ ist eine unabhängige Menge recht schnell modelliert: jeder Knoten $u$ kriegt eine Variable $x_u$, und jede Kante $\{u,v\}$ kriegt eine Klausel $(\bar{x}_u \vee \bar{x}_v)$. Schwieriger wird es, die Aussage $I$ hat $k$ Elemente zu formalisieren. Ich empfehle Ihnen, großzügig mit Variablen zu sein und $kn$ zusätzliche Variable einzuführen.

Übungsaufgabe Sei $G = (V,E)$. Ein Hamiltonscher Pfad ist ein Pfad in $G$ mit $|V|-1$ Kanten (und $|V|$ Knoten). Also ein Pfad, der jeden Knoten genau einmal besucht. Hamilton Path ist das Entscheidungsproblem: Gegeben ein Graph, hat er einen Hamiltonschen Pfad?

Modellieren Sie Hamilton Path als CNF. Das ist etwas schwieriger. Fragen Sie mich gerne nach einen Tip.

Übungsaufgabe Sokoban ist ein japanisches Computerspiel aus dem Jahre 1982, in dem ein Lagerhausverwalter (japanisch 倉庫番, Sōkoban) Kisten auf bestimmte Zielplätze schieben muss.


Bildquelle: wikimedia
Das wird dadurch schwierig, dass er die Kisten (1) nicht ziehen kann, (2) nicht zwei aufs Mal schieben und (3) nicht über die Kisten klettern kann. Sokoban ist das Entscheidungsproblem, ob ein gegebenes Puzzle eine Lösung hat.

Versuchen Sie, Sokoban als CNF zu modellieren. Welchen Schwierigkeiten begegnen Sie? Was ist einfach nur mühsam und wo stoßen Sie auf fundamentale Schwierigkeiten?

Übungsaufgabe Hex ist ein Brettspiel für zwei Personen, bei denen jeder Spieler seine zwei Seiten mit seinen Steinen zu verbinden sucht. Hier ist das leere Brett:

Blau beginnt. Die Spieler legen abwechselnd Steine. Hier sind wir nach dreieinhalb Zügen:

Als nächstes ist Rot am Zug. Kann Rot den Sieg erzwingen? Ich habe aus Spaß zu Ende gespielt. Rot hat gewonnen, da es die beiden roten Ränder mit roten Steinen verbunden hat:

Hier ist nun Hex als Entscheidungsproblem Red Win in Hex: gegeben ein teilweise gefülltes Hex-Brett, in welchem Rot am Zug ist. Kann Rot den Sieg erzwingen, wenn beide Spieler optimal spielen?

Versuchen Sie, dies mit SAT zu modellieren. Sie werden scheitern. Warum?

Können Sie die Frage: Rot kann den Sieg in einem Zug erreichen mit SAT modellieren?