DSA-Signaturen

Das im Folgenden betrachtete Verfahren DSA (Digital Signature Algorithm) - auch bekannt als U.S. Federal Information Processing Standard 186 unter dem Namen DSS (Digital Signature Standard) - ist eine Variante des ElGamal-Schemas und verlangt explizit die Verwendung von SHA-1 als Hashalgorithmus. Im Gegensatz zu RSA-Signaturen, deren Sicherheit auf dem Problem der Primfaktorenzerlegung großer Zahlen beruht, basieren DSA-Signaturen darauf, dass die Berechnung diskreter Logarithmen in für große Primzahlen nicht mit realistischem Zeitaufwand zu bewältigen ist.

Schlüsselgenerierung

1. A wählt eine Primzahl , sodass gilt.
2. A wählt eine zweite Primzahl mit und . Die Wahl muss außerdem so erfolgen, dass ein Teiler von ist.
3. (Bestimme erzeugendes Element der zyklischen Untergruppe mit Ordnung in )
   1. A bestimmt ein , berechnet und
   2. wiederholt diesen Schritt bis ist.
4. A wählt ein zufälliges mit .
5. A berechnet .

Das Tupel wird von A als öffentlicher Schlüssel bekanntgegeben und die Zahl stellt den zugehörigen geheimen Schlüssel dar.

Signatur erstellen

Um eine Nachricht zu signieren, werden folgende Schritte ausgeführt:

1. A wählt ein zufälliges mit .
2. A berechnet .
3. A bestimmt mit dem erweiterten Euklidischen Algorithmus das Inverse ,
   d.h. die Zahl für die gilt: .
4. A berechnet .

Das Paar bildet nun die Signatur der Nachricht .

Signatur prüfen

Unter Verwendung des öffentlichen Schlüssels von A kann B wie folgt eine Signatur 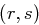einer Nachricht prüfen:

1. B verwirft die Signatur, falls oder nicht erfüllt ist.
2. B berechnet
3. B ermittelt und .
4. B berechnet .

Die Signatur wird nur dann als gültig erkannt, wenn gilt.

Korrektheit

Wenn das Tupel eine gültige Signatur darstellt, so gilt:

Beispiel

Am Beispiel des ASCII-Strings "DSA ist ein im OpenPGP-Standard enthaltener Algorithmus." soll das Verfahren demonstriert werden. Dieser Satz besitzt als SHA-1 Hashwert - DSA schreibt die Verwendung von SHA-1 vor - die Zeichenkette AB00 EB6A FD5F 6308 8352 9F98 AE96 0F93 8A10 7F28 (eine 160 Bits lange Binärzahl in Hexadezimalschreibweise). Um die Berechnungen nicht unnötig zu verkomplizieren, werden wir in dem Beispiel nur die letzten 16 Bits, d.h. 7F28, verwenden. Die zu signierende Nachricht ist der Hashwert als Dezimalzahl, in unserem Fall also .

Schlüsselgenerierung.
Die für dieses Beispiel verwendeten Primzahlen sind ebenfalls kleiner als verlangt, hier wählen wir und , somit folgt daraus, dass . Sei , dann ergibt sich

Der geheime Schlüssel ist und der letzte Teil des öffentlichen Schlüssels berechnet sich wie folgt

Signatur erstellen.
Für die Erstellung benötigen wir eine geheime, zufällig gewählte Zahl , in diesem Beispiel sei . Den ersten Teil der Signatur erhalten wir nun als

Für den zweiten Teil ermitteln wir das multiplikative Inverse und berechnen damit

Die Signatur für die Nachricht ist damit das Paar .

Signatur prüfen.
Die Prüfung der Signatur erfolgt mit folgenden Berechnungen:

Die Berechnungen liefern und wir akzeptieren die als gültig erkannte Signatur.