Allgemeine Methoden
Blockchiffren
Flusschiffren (Stream Ciphers)
Chaining (CBC-Modus, Cipher Block Chaining Mode)
CFB-Modus (Cipher Feedback Mode)
Kombination von Kryptosystemen
Wir stellen im Folgenden einige Klassen von allgemeinen Methoden der Ver- und Entschlüsselung vor. Dies soll dazu dienen, ein Gefühl für mögliche kryptographische Ansätze und Verfahren zu bekommen.
Blockchiffren
Die Blockchiffren wurden bereits im Abschnitt über Klassische Kryptographie erwähnt. An dieser Stelle geben wir noch eine formale Definition dieser Methode.
Seien 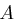 und
und 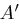 endliche Alphabete, es gelte
endliche Alphabete, es gelte 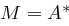 ,
, 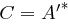 und es sei
und es sei 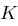 eine endliche Menge von Schlüsseln. Eine Chiffrierfunktion
eine endliche Menge von Schlüsseln. Eine Chiffrierfunktion 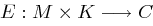 heißt
heißt 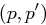 -Blockchiffre, wenn es eine Funktion
-Blockchiffre, wenn es eine Funktion 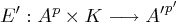 gibt, wobei
gibt, wobei 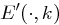 für jeden Schlüssel
für jeden Schlüssel 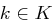 injektiv ist, so dass gilt: Für jede Nachricht
injektiv ist, so dass gilt: Für jede Nachricht 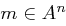 der Länge
der Länge 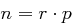 zerlegt in Blöcke
zerlegt in Blöcke  der Länge jeweils
der Länge jeweils 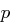 ist
ist
Ist 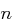 nicht durch
nicht durch 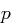 teilbar, so fülle die Nachricht
teilbar, so fülle die Nachricht 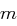 beliebig bis Länge
beliebig bis Länge 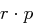 auf. Das Chiffrat
auf. Das Chiffrat 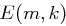 hat die Länge
hat die Länge 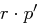 .
.
Der Nachteil bei 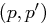 -Blockchiffren ist, dass gleiche Klartextblöcke gleiche Kryptogramme erzeugen können. Regelmäßig auftretende Textmuster findet man dann im Kryptogramm wieder. Ein Vorteil ist hingegen, dass z.B. Bitumkehrfehler, etwa bei einer Störung der Übertragung, isoliert bleiben und nur einen Block unbrauchbar machen. Die Cäsar Chiffren sind
-Blockchiffren ist, dass gleiche Klartextblöcke gleiche Kryptogramme erzeugen können. Regelmäßig auftretende Textmuster findet man dann im Kryptogramm wieder. Ein Vorteil ist hingegen, dass z.B. Bitumkehrfehler, etwa bei einer Störung der Übertragung, isoliert bleiben und nur einen Block unbrauchbar machen. Die Cäsar Chiffren sind 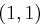 -Blockchiffren, wie wir noch sehen werden.
-Blockchiffren, wie wir noch sehen werden.
Flusschiffren (Stream Ciphers)
Im Gegensatz zu den Blockchiffren verwenden Flusschiffren für jeden zu verschlüsselnden Buchstaben einen anderen Schlüssel. Sei etwa 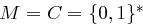 und eine endliche Schlüsselmenge, etwa
und eine endliche Schlüsselmenge, etwa 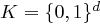 gegeben. Ein Schlüssel
gegeben. Ein Schlüssel 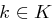 wird als Eingabe für einen deterministischen "Zufallszahlengenerator" verwendet, der eine im Prinzip beliebig lange Ausgabefolge
wird als Eingabe für einen deterministischen "Zufallszahlengenerator" verwendet, der eine im Prinzip beliebig lange Ausgabefolge 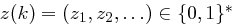 produziert.
produziert.
Eine Nachricht 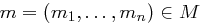 wird verschlüsselt mit
wird verschlüsselt mit
Die Entschlüsselung geschieht dann mit
Hierbei ist  das Exklusiv-Oder. Ein Vorteil von Flusschiffren ist, dass Buchstaben/Blöcke positionsabhängig verschlüsselt werden, also gleiche Buchstaben teilweise mit verschiedenen
das Exklusiv-Oder. Ein Vorteil von Flusschiffren ist, dass Buchstaben/Blöcke positionsabhängig verschlüsselt werden, also gleiche Buchstaben teilweise mit verschiedenen 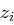 .
.
Chaining (CBC-Modus, Cipher Block Chaining Mode)
Beim Chaining vermeidet man das Auftreten regelmäßiger Muster. Die Verschlüsselung eines Blockes hängt von allen vorherigen Blöcken ab. Eine Nachricht 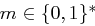 wird zunächst in Blöcke
wird zunächst in Blöcke 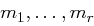 jeweils der Länge
jeweils der Länge 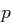 zerlegt. Die Verschlüsselung erfolgt auf diesen Blöcken mittels einer Verschlüsselungsfunktion
zerlegt. Die Verschlüsselung erfolgt auf diesen Blöcken mittels einer Verschlüsselungsfunktion 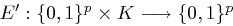 .
.
Nun wählt man zusätzlich zu dem Schlüssel 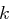 eine Initialisierungsfolge
eine Initialisierungsfolge 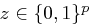 und bildet das Chiffrat
und bildet das Chiffrat 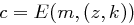 mit
mit
wobei 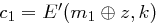 und im Allgemeinen
und im Allgemeinen 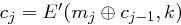 gilt. Für die Dechiffrierfunktion
gilt. Für die Dechiffrierfunktion 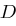 gilt dann
gilt dann
mit 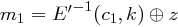 und
und 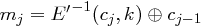 . Hierbei ist
. Hierbei ist 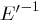 die Umkehrfunktion zu
die Umkehrfunktion zu 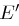 .
.
Im Allgemeinen werden gleiche Klartextblöcke verschieden verschlüsselt, da der Kryptogrammblock 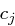 von der Verschlüsselung des Nachrichtenblocks
von der Verschlüsselung des Nachrichtenblocks 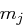 und allen vorhergehenden Nachrichtenblöcken
und allen vorhergehenden Nachrichtenblöcken 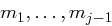 abhängt. Es ist nicht möglich, nur einzelne Kryptogrammblöcke, etwa in der Mitte, zu entschlüsseln. Ein Bitumkehrfehler in
abhängt. Es ist nicht möglich, nur einzelne Kryptogrammblöcke, etwa in der Mitte, zu entschlüsseln. Ein Bitumkehrfehler in 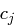 wirkt sich möglicherweise auf die Entschlüsselung der Nachrichtenblöcke
wirkt sich möglicherweise auf die Entschlüsselung der Nachrichtenblöcke 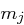 und
und 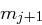 aus, aber nicht auf die folgenden Blöcke
aus, aber nicht auf die folgenden Blöcke 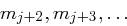 .
.
CFB-Modus (Cipher Feedback Mode)
Eine Beschleunigung der Entschlüsselung der Chiffrate beim Empfänger gegenüber dem CBC-Modus erhalten wir mit dem folgend beschriebenen Verfahren. Beim CBC-Modus können nämlich Ver- und Entschlüsselung nur nacheinander ausgeführt werden, was bei zeitaufwändigen Berechnungen ein Problem sein kann.
Man wählt einen Initialisierungsvektor 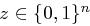 der Länge
der Länge 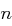 . Dann wird eine Zahl
. Dann wird eine Zahl 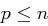 fixiert. Eine Nachricht
fixiert. Eine Nachricht 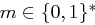 wird in Blöcke
wird in Blöcke  jeweils der Länge
jeweils der Länge 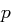 zerlegt. Gegeben ist eine Chiffrierfunktion
zerlegt. Gegeben ist eine Chiffrierfunktion 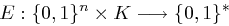 mit der endlichen Schlüsselmenge
mit der endlichen Schlüsselmenge 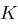 , die Sender und Empfänger kennen.
, die Sender und Empfänger kennen.
Anfangs setzt man 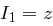 und führt zur Verschlüsselung der Blöcke
und führt zur Verschlüsselung der Blöcke 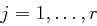 die folgenden Schritte durch:
die folgenden Schritte durch:
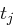 = erste
= erste 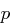 Bits von
Bits von 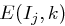
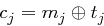
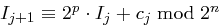 .
.
(Man entfernt die ersten 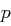 Bits von
Bits von 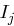 , schiebt die verbleibenden Bits nach "links" und an den
, schiebt die verbleibenden Bits nach "links" und an den 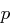 freigewordenen niederwertigen Positionen fügt man die Bits von
freigewordenen niederwertigen Positionen fügt man die Bits von 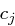 ein.)
ein.)
Der Empfänger geht analog vor und setzt 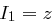 und führt für
und führt für 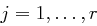 die folgenden Schritte aus:
die folgenden Schritte aus:
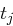 = erste
= erste 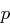 Bits von
Bits von 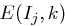
- Berechne
 , erhalte hiermit
, erhalte hiermit 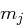
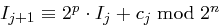 .
.
Der Vorteil ist, dass Sender und Empfänger gleichzeitig 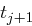 berechnen können, sobald
berechnen können, sobald 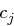 bekannt ist.
bekannt ist.
Kombination von Kryptosystemen
Verschiedene oder auch gleiche Kryptosysteme können kombiniert werden, beispielsweise durch Komposition (Hintereinanderausführung) oder Produktbildung. Die Komposition zweier Kryptosysteme 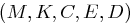 und
und 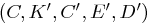 ergibt ein System
ergibt ein System 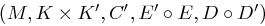 , wobei die Verschlüsselung mit der folgenden Funktion geschieht
, wobei die Verschlüsselung mit der folgenden Funktion geschieht
und die Entschlüsselung mit der Funktion
Die Systeme werden also nacheinander auf den entstehenden unverschlüsselten bzw. verschlüsselten Text angewendet.
Als das Produkt zweier Kryptosysteme 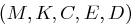 und
und 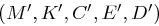 ergibt sich das System
ergibt sich das System 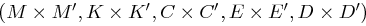 mit
mit
und
Es wird also auf eine linke und rechte Hälfte getrennt voneinander das erste bzw. das zweite Kryptosystem angewendet.
Als Beispiel für die Komposition zweier Kryptosysteme betrachten wir die Komposition zweier Cäsar-Chiffren. Man erhält als Verschlüsselungsfunktion 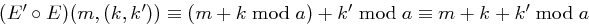 , man erhält also wieder eine Cäsar-Chiffre.
, man erhält also wieder eine Cäsar-Chiffre.
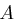 und
und 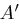 endliche Alphabete, es gelte
endliche Alphabete, es gelte 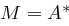 ,
, 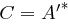 und es sei
und es sei 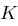 eine endliche Menge von Schlüsseln. Eine Chiffrierfunktion
eine endliche Menge von Schlüsseln. Eine Chiffrierfunktion 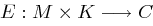 heißt
heißt 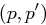 -Blockchiffre, wenn es eine Funktion
-Blockchiffre, wenn es eine Funktion 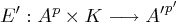 gibt, wobei
gibt, wobei 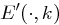 für jeden Schlüssel
für jeden Schlüssel 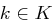 injektiv ist, so dass gilt: Für jede Nachricht
injektiv ist, so dass gilt: Für jede Nachricht 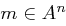 der Länge
der Länge 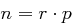 zerlegt in Blöcke
zerlegt in Blöcke  der Länge jeweils
der Länge jeweils 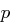 ist
ist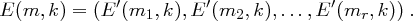
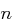 nicht durch
nicht durch 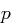 teilbar, so fülle die Nachricht
teilbar, so fülle die Nachricht 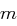 beliebig bis Länge
beliebig bis Länge 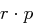 auf. Das Chiffrat
auf. Das Chiffrat 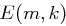 hat die Länge
hat die Länge 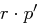 .
.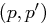 -Blockchiffren ist, dass gleiche Klartextblöcke gleiche Kryptogramme erzeugen können. Regelmäßig auftretende Textmuster findet man dann im Kryptogramm wieder. Ein Vorteil ist hingegen, dass z.B. Bitumkehrfehler, etwa bei einer Störung der Übertragung, isoliert bleiben und nur einen Block unbrauchbar machen. Die Cäsar Chiffren sind
-Blockchiffren ist, dass gleiche Klartextblöcke gleiche Kryptogramme erzeugen können. Regelmäßig auftretende Textmuster findet man dann im Kryptogramm wieder. Ein Vorteil ist hingegen, dass z.B. Bitumkehrfehler, etwa bei einer Störung der Übertragung, isoliert bleiben und nur einen Block unbrauchbar machen. Die Cäsar Chiffren sind 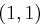 -Blockchiffren, wie wir noch sehen werden.
-Blockchiffren, wie wir noch sehen werden.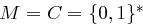 und eine endliche Schlüsselmenge, etwa
und eine endliche Schlüsselmenge, etwa 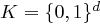 gegeben. Ein Schlüssel
gegeben. Ein Schlüssel 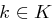 wird als Eingabe für einen deterministischen "Zufallszahlengenerator" verwendet, der eine im Prinzip beliebig lange Ausgabefolge
wird als Eingabe für einen deterministischen "Zufallszahlengenerator" verwendet, der eine im Prinzip beliebig lange Ausgabefolge 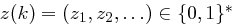 produziert.
produziert.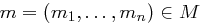 wird verschlüsselt mit
wird verschlüsselt mit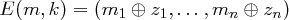
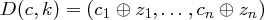
 das Exklusiv-Oder. Ein Vorteil von Flusschiffren ist, dass Buchstaben/Blöcke positionsabhängig verschlüsselt werden, also gleiche Buchstaben teilweise mit verschiedenen
das Exklusiv-Oder. Ein Vorteil von Flusschiffren ist, dass Buchstaben/Blöcke positionsabhängig verschlüsselt werden, also gleiche Buchstaben teilweise mit verschiedenen 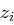 .
.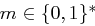 wird zunächst in Blöcke
wird zunächst in Blöcke 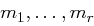 jeweils der Länge
jeweils der Länge 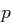 zerlegt. Die Verschlüsselung erfolgt auf diesen Blöcken mittels einer Verschlüsselungsfunktion
zerlegt. Die Verschlüsselung erfolgt auf diesen Blöcken mittels einer Verschlüsselungsfunktion 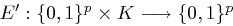 .
.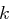 eine Initialisierungsfolge
eine Initialisierungsfolge 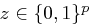 und bildet das Chiffrat
und bildet das Chiffrat 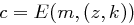 mit
mit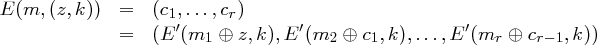
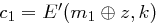 und im Allgemeinen
und im Allgemeinen 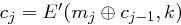 gilt. Für die Dechiffrierfunktion
gilt. Für die Dechiffrierfunktion 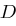 gilt dann
gilt dann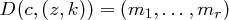
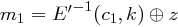 und
und 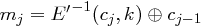 . Hierbei ist
. Hierbei ist 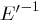 die Umkehrfunktion zu
die Umkehrfunktion zu 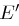 .
.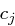 von der Verschlüsselung des Nachrichtenblocks
von der Verschlüsselung des Nachrichtenblocks 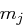 und allen vorhergehenden Nachrichtenblöcken
und allen vorhergehenden Nachrichtenblöcken 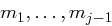 abhängt. Es ist nicht möglich, nur einzelne Kryptogrammblöcke, etwa in der Mitte, zu entschlüsseln. Ein Bitumkehrfehler in
abhängt. Es ist nicht möglich, nur einzelne Kryptogrammblöcke, etwa in der Mitte, zu entschlüsseln. Ein Bitumkehrfehler in 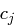 wirkt sich möglicherweise auf die Entschlüsselung der Nachrichtenblöcke
wirkt sich möglicherweise auf die Entschlüsselung der Nachrichtenblöcke 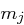 und
und 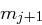 aus, aber nicht auf die folgenden Blöcke
aus, aber nicht auf die folgenden Blöcke 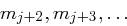 .
.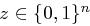 der Länge
der Länge 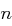 . Dann wird eine Zahl
. Dann wird eine Zahl 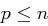 fixiert. Eine Nachricht
fixiert. Eine Nachricht 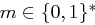 wird in Blöcke
wird in Blöcke  jeweils der Länge
jeweils der Länge 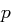 zerlegt. Gegeben ist eine Chiffrierfunktion
zerlegt. Gegeben ist eine Chiffrierfunktion 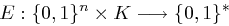 mit der endlichen Schlüsselmenge
mit der endlichen Schlüsselmenge 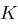 , die Sender und Empfänger kennen.
, die Sender und Empfänger kennen.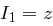 und führt zur Verschlüsselung der Blöcke
und führt zur Verschlüsselung der Blöcke 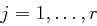 die folgenden Schritte durch:
die folgenden Schritte durch: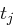 = erste
= erste 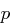 Bits von
Bits von 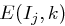
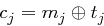
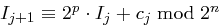 .
.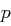 Bits von
Bits von 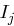 , schiebt die verbleibenden Bits nach "links" und an den
, schiebt die verbleibenden Bits nach "links" und an den 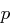 freigewordenen niederwertigen Positionen fügt man die Bits von
freigewordenen niederwertigen Positionen fügt man die Bits von 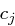 ein.)
ein.)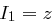 und führt für
und führt für 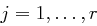 die folgenden Schritte aus:
die folgenden Schritte aus: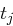 = erste
= erste 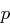 Bits von
Bits von 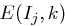
 , erhalte hiermit
, erhalte hiermit 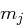
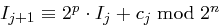 .
.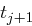 berechnen können, sobald
berechnen können, sobald 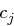 bekannt ist.
bekannt ist.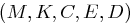 und
und 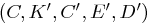 ergibt ein System
ergibt ein System 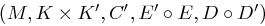 , wobei die Verschlüsselung mit der folgenden Funktion geschieht
, wobei die Verschlüsselung mit der folgenden Funktion geschieht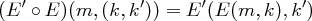
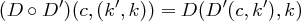
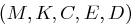 und
und 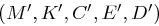 ergibt sich das System
ergibt sich das System 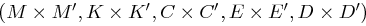 mit
mit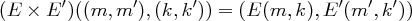
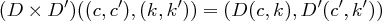
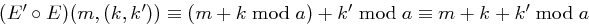 , man erhält also wieder eine Cäsar-Chiffre.
, man erhält also wieder eine Cäsar-Chiffre.