Auflösung des Gleichungssystems

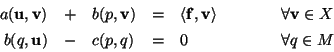
Gemischte Formulierung:

$$\begin{array}{rclclll} a(\mathbf{u},\mathbf{v}) & + & b(p,\ma... ...bf{u}) & - & c(p,q) & = & 0 &\qquad&\forall q\in M \end{array}$$

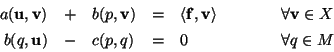
FE-Gleichungssystem:

$$\left[ \begin{array}{cc} A & B \\ [1ex] B^T & -C \end{array} ... ...y}{c} \underline{f} \\ [1ex] \underline{0} \end{array} \right]$$

$A$, $C$ positiv definit, Gesamtsystem indefinit.

Bramble-Pasciak-Idee:
nach Modifikation durch A. Meyer: Für

$${\cal A} = \left[ \begin{array}{cc} A_0^{-1} & O \\ [1ex] \... ... \begin{array}{cc} A & B \\ [1ex] B^T & -C \end{array} \right]$$

mit $A_0 \sim A$, $B_0 \sim B^T A_0^{-1} B + C$ gilt:

$$\langle {\cal A} x,y \rangle_P = \langle x, {\cal A} y \rangle_P, \qquad \langle {\cal A} x,x \rangle_P \ge 0,$$

d.h., ${\cal A}$ ist s.p.d. im durch $P = \mbox{\small$\left[ \begin{array}{c@{}c} A-\gamma A_0 & O \\ [1ex] O & \delta^{-1}B_0 \end{array} \right]$}$

definierten Skalarprodukt. CG ist anwendbar.

Beispiel: ebenes Elastizitätsproblem

$$E = \left\{ \begin{array}{r@{\quad\mbox{in }}l} 200\,000 & ... ...in }}l} 0.3 & \Omega_1 \\ 0.5 & \Omega_2 \end{array} \right.$$

Isolinien von u_x:

Lösung mit Q_1,h/2/Q₁-Element,
A₀, B₀ durch hierarschische Basen

Rechnung auf p Prozessoren:

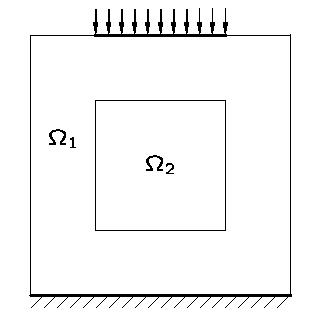
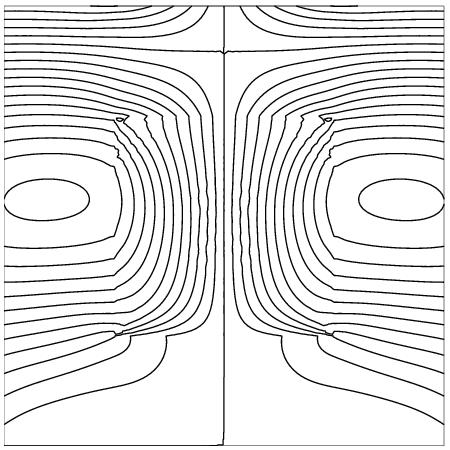
Level	3	4	5	6	7
Iterationen	314	331	348	377	414
Iter. bei nu2=0.45	86	88	91	94	99
Zeit p=1	4.0	21.0	88.8	-	-
Zeit p=2	2.6	10.8	46.4	191.2	-
Zeit p=4	1.8	5.6	23.1	96.1	-
Zeit p=8	1.4	3.4	11.7	49.0	202.8
Zeit p=16	1.5	2.5	6.2	25.1	103.6
Zeit p=32	1.6	2.2	4.2	12.9	55.3
N	12 675	...	...	...	3 151 875