| Zeit: |
Donnerstag, 21.01.1999, 09:00 Uhr |
| Ort: |
Reichenhainer Straße 70, B201 |
| Vortragender: |
Prof. L. Tobiska
(Magdeburg) |
| Thema: |
Properties of the Streamline-Diffusion
Finite Element Method on a Shishkin Mesh for Singularly Perturbed
Elliptic Equations with Exponential Layers
|
On the unit square, we consider a singularly perturbed
convection-diffusion boundary value problem whose solution has exponential
boundary layers along two sides of the square.
We use the streamline-diffusion finite element method (SDFEM) with piecewise
bilinear trial functions on a Shishkin mesh of O(N2)
points and show that it is convergent, uniformly in the diffusion parameter
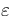 , of order , of order
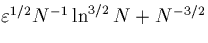 to its bilinear interpolant in the usual streamline-diffusion norm.
As a corollary we prove that the method is convergent of order
to its bilinear interpolant in the usual streamline-diffusion norm.
As a corollary we prove that the method is convergent of order
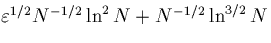 (again uniformly in
(again uniformly in
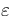 ) in the local ) in the local
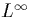 norm on the
fine part of the mesh (i.e., inside the boundary layers). This local norm on the
fine part of the mesh (i.e., inside the boundary layers). This local
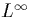 estimate within the layers can be improved to order estimate within the layers can be improved to order
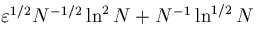 , uniformly in , uniformly in
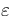 , away from the corner layer.
We present numerical results to support these results and to examine the
effect of replacing bilinear trials with linear trials in the SDFEM. , away from the corner layer.
We present numerical results to support these results and to examine the
effect of replacing bilinear trials with linear trials in the SDFEM.
|
|
Interessenten sind herzlich eingeladen. |
![[SFB-Logo]](../../GIF/sfb393m.gif)